Содержание
- 2. План выступления История и предпосылки к созданию вейвлет-преобразования Определение вейвлет-преобразования, его разновидности.Теория Практические примеры использования вейвлет-преобразования
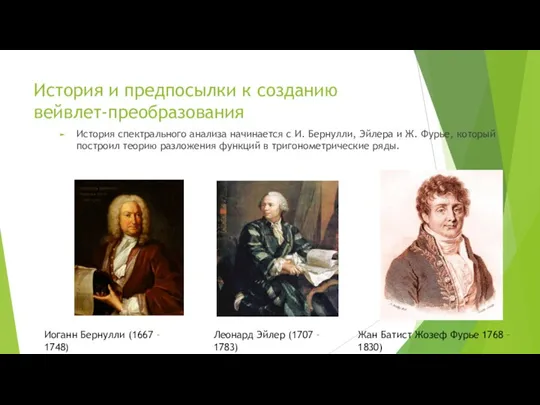
- 3. История и предпосылки к созданию вейвлет-преобразования История спектрального анализа начинается с И. Бернулли, Эйлера и Ж.
- 4. История и предпосылки к созданию вейвлет-преобразования
- 5. Определение вейвлет-преобразования, его разновидности. Теория.
- 6. Определение вейвлет-преобразования, его разновидности. Теория.
- 7. Определение вейвлет-преобразования, его разновидности. Теория.
- 8. Определение вейвлет-преобразования, его разновидности. Теория. Дискретное вейвлет-преобразование (DWT) Приведенное выше разложение вдвое уменьшает разрешение по времени
- 9. Определение вейвлет-преобразования, его разновидности. Теория. Принцип вейвлет преобразования Гармонические функции локализованы в частотной области и нелокализованы
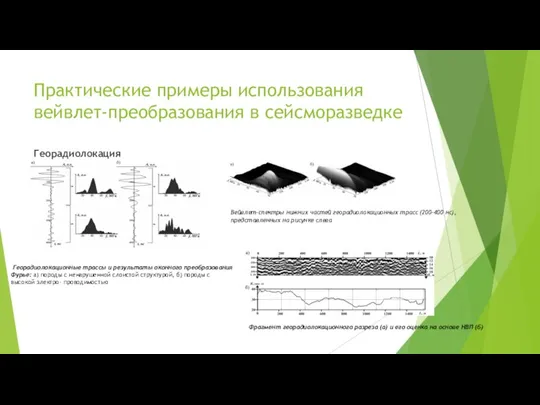
- 10. Практические примеры использования вейвлет-преобразования в сейсморазведке Георадиолокация Георадиолокационные трассы и результаты оконного преобразования Фурье: а) породы
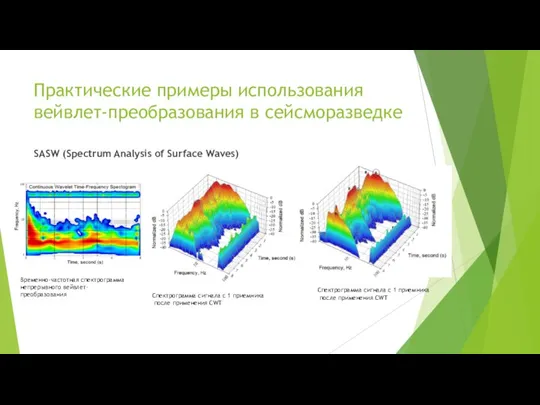
- 11. Практические примеры использования вейвлет-преобразования в сейсморазведке SASW (Spectrum Analysis of Surface Waves) Сейсмотрассы, полученные на 8
- 12. Практические примеры использования вейвлет-преобразования в сейсморазведке SASW (Spectrum Analysis of Surface Waves) Временно-частотная спектрограмма непрерывного вейвлет-преобразования
- 13. Практические примеры использования вейвлет-преобразования в сейсморазведке Два случая применения вейвлет-преобразования при обработке сейсмических данных До применения
- 14. Вопросы к зачету: 1) Когда появился вейвлет-анализ, в связи с чем и когда он получил широкое
- 15. Список используемых материалов Успехи и перспективы приенения вейвлетных преобразований для анализа нестационарных нелинейных данных в современной
- 17. Скачать презентацию











 Зона арктических пустынь. Тундра
Зона арктических пустынь. Тундра Ордынский район. Доволенский район. Климатическая карта
Ордынский район. Доволенский район. Климатическая карта Основные понятия гидрогеологии
Основные понятия гидрогеологии Изолинии. Виды изолиний
Изолинии. Виды изолиний Природные ресурсы России
Природные ресурсы России Речка Крынка
Речка Крынка Финский залив – жемчужина Балтики. Визитка: вода Финского залива для жизни нам необходима
Финский залив – жемчужина Балтики. Визитка: вода Финского залива для жизни нам необходима Земля
Земля Пещера Кызыл-Яровская
Пещера Кызыл-Яровская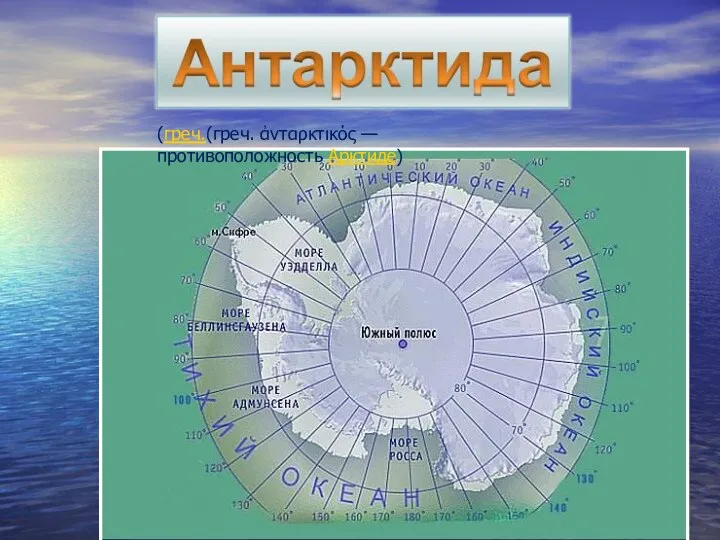 Материк Антарктида
Материк Антарктида Saksa on suurin maa Euroopassa
Saksa on suurin maa Euroopassa
 Греция
Греция Солнечная энергия и температура воздуха
Солнечная энергия и температура воздуха Почвы России
Почвы России Геоинформационные реусрсы
Геоинформационные реусрсы Зависимость рек от климата
Зависимость рек от климата Правило оформления крупномасштабных ландшафтных карт
Правило оформления крупномасштабных ландшафтных карт Парк Природы Валаамский архипелаг
Парк Природы Валаамский архипелаг Открытие Австралии и островов Тихого океана
Открытие Австралии и островов Тихого океана Германия
Германия Студенты РУК в солнечной Полтаве
Студенты РУК в солнечной Полтаве Китай (КНР)
Китай (КНР) Экскурсия по странам Азии
Экскурсия по странам Азии Ландшафты Дубая
Ландшафты Дубая 358545
358545 Ориентирование на местности по топографической карте
Ориентирование на местности по топографической карте Поездка на озеро Байкал
Поездка на озеро Байкал