Содержание
- 2. Виды измерений Измерение – процесс сравнения какой-либо величины с другой однородной величиной, принимаемой за единицу Виды
- 3. Единицы измерения МЕТР За единицу линейных и высотных измерений (расстояний, высот и превышений) принят метр (от
- 4. Виды измерений: Измерения называют: прямыми, если их выполняют с помощью приборов, позволяющих непосредственно сравнить измеряемую величину
- 5. Условия измерений: объект измерения; субъект измерения - лицо, производящее измерение; мерный прибор, которым выполняют измерения; метод
- 6. Обозначенные на местности точки: Обозначенные на местности точки, от которых выполняют геодезические измерения, называются исходными. Точки,
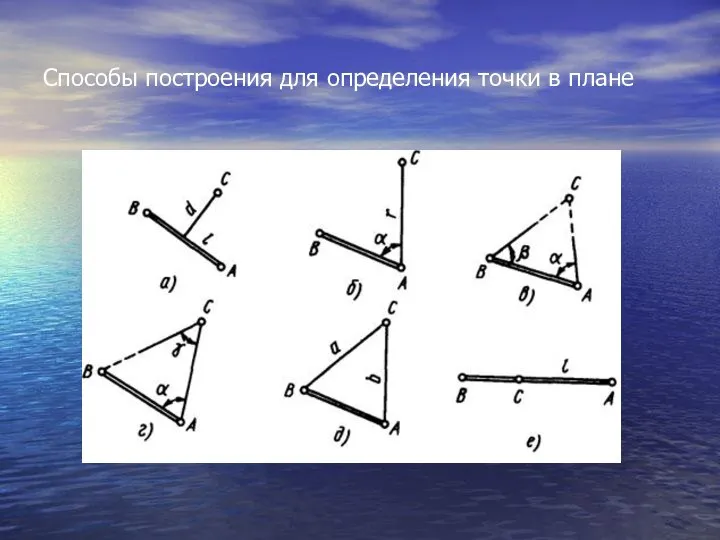
- 7. Способы построения для определения точки в плане
- 8. Способы построения для определения точки в плане а) Положение точки С можно определить, если опустить из
- 10. Скачать презентацию






 Презентация на тему Путешествие по Швейцарии
Презентация на тему Путешествие по Швейцарии  Кугешнем тый денет, шочмо ялем!
Кугешнем тый денет, шочмо ялем! Многоликая Бразилия
Многоликая Бразилия Животный и растительный мир Дальнего Востока
Животный и растительный мир Дальнего Востока Рельеф суши
Рельеф суши 20141120_chislennost_naseleniya_rossii
20141120_chislennost_naseleniya_rossii The best sights are mostly concentrated in the capital of Singapore and its surrounding surroundings
The best sights are mostly concentrated in the capital of Singapore and its surrounding surroundings Слуцкие пояса
Слуцкие пояса 20141106_pustyni_rossii
20141106_pustyni_rossii Дербент - самый древний город России
Дербент - самый древний город России Tour around London. London Eye
Tour around London. London Eye Основные биомы суши. Зона тайги
Основные биомы суши. Зона тайги Приморский край
Приморский край Смена дня и ночи
Смена дня и ночи Путешествуем по Лешуконскому району длиною 120 километров
Путешествуем по Лешуконскому району длиною 120 километров Модели ресурсопользования
Модели ресурсопользования Ориентирование на местности
Ориентирование на местности Австралия
Австралия Парк призрачного поезда Лима, Перу
Парк призрачного поезда Лима, Перу Природные зоны
Природные зоны Земная кора
Земная кора Анализ условий для развития хозяйства Европейского Юга
Анализ условий для развития хозяйства Европейского Юга 20140314_kak_budet_vigladet_zemla_2006
20140314_kak_budet_vigladet_zemla_2006 Оттек және озон
Оттек және озон Якшур-Бодьинский район
Якшур-Бодьинский район Германия
Германия 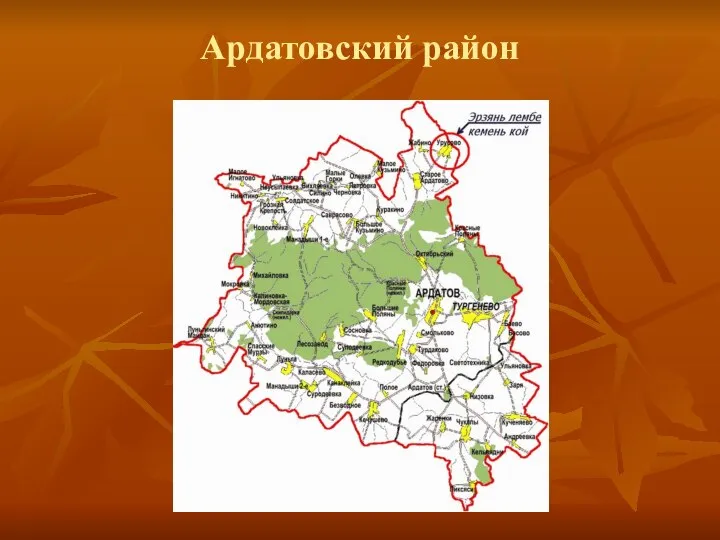 Ардатовский район
Ардатовский район Как люди заселяли Землю
Как люди заселяли Землю