Содержание
- 2. Сферические координаты (координаты точек на поверхности сферы или эллипсоида)
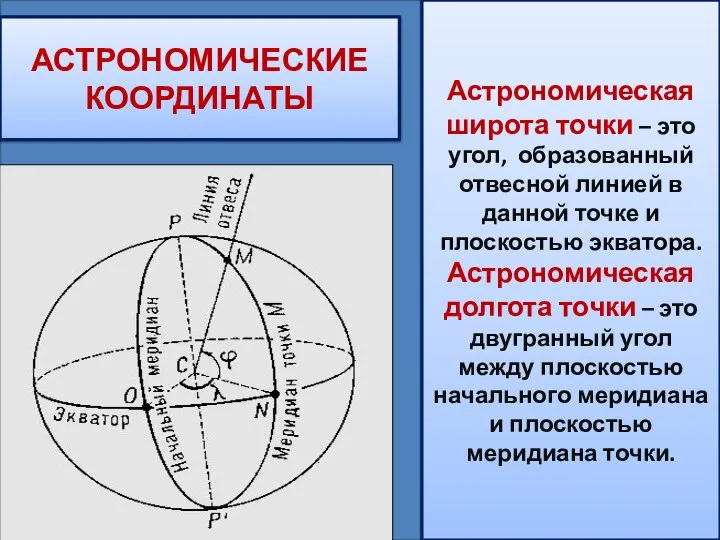
- 3. АСТРОНОМИЧЕСКИЕ КООРДИНАТЫ Астрономическая широта точки – это угол, образованный отвесной линией в данной точке и плоскостью
- 4. Гринвичский меридиан
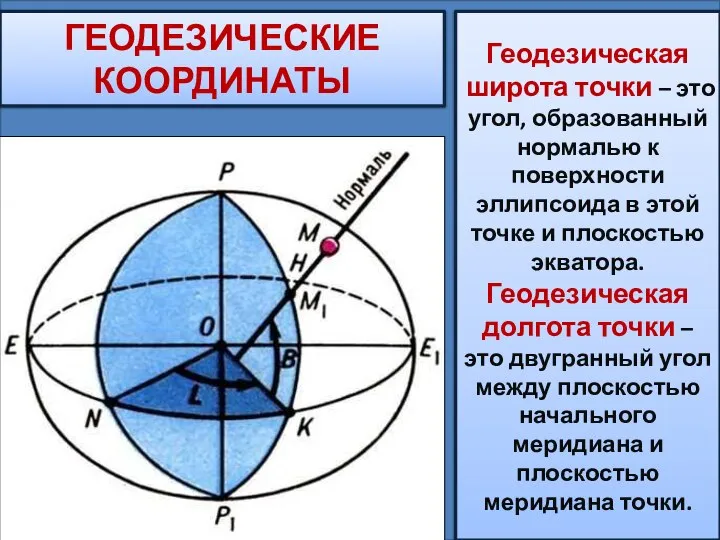
- 5. ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ Геодезическая широта точки – это угол, образованный нормалью к поверхности эллипсоида в этой точке
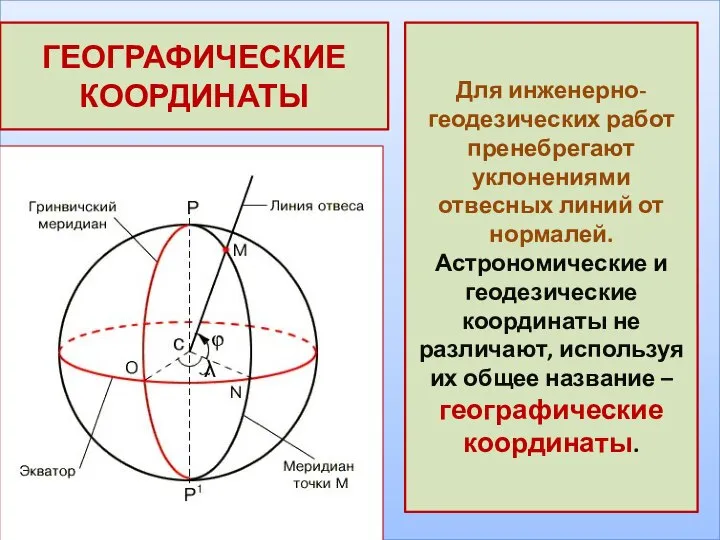
- 6. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ Для инженерно-геодезических работ пренебрегают уклонениями отвесных линий от нормалей. Астрономические и геодезические координаты не
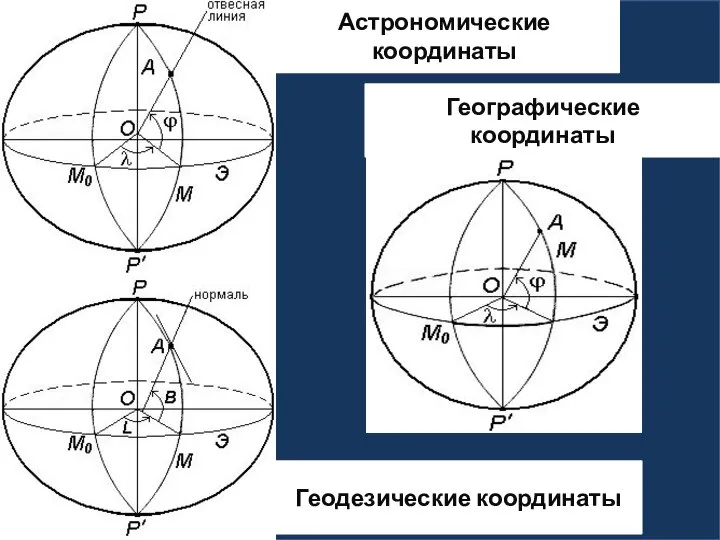
- 7. Астрономические координаты Геодезические координаты Географические координаты
- 8. Плоские координаты (координаты точек на плоскости)
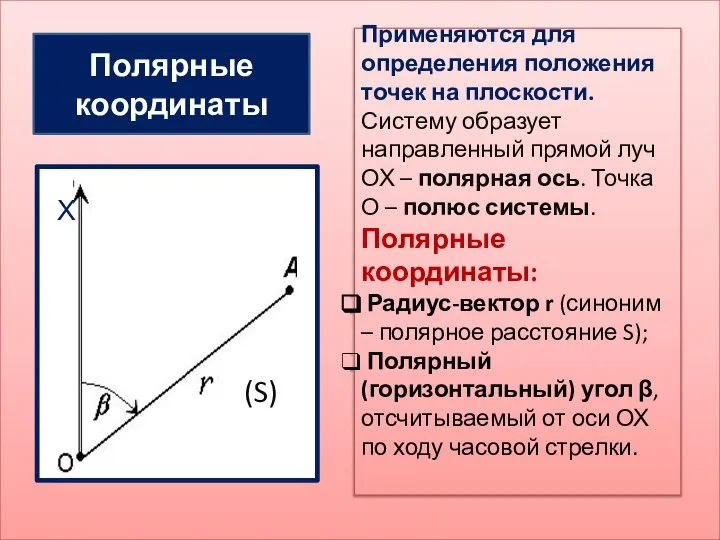
- 9. (S) Полярные координаты Применяются для определения положения точек на плоскости. Систему образует направленный прямой луч ОХ
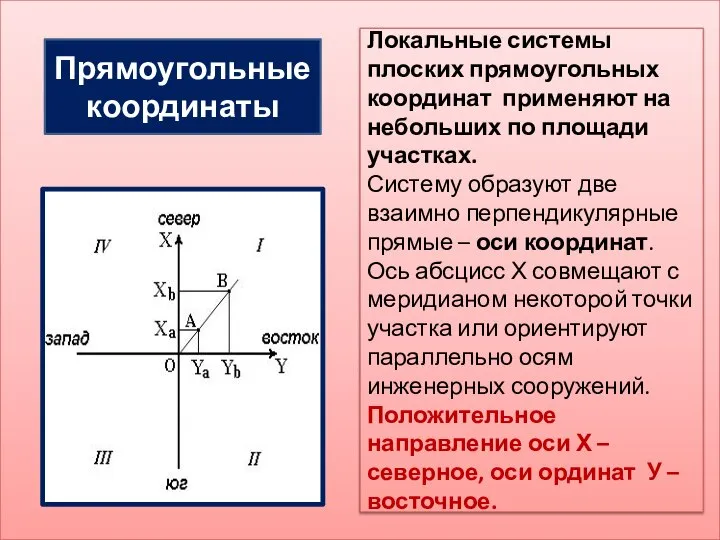
- 10. Прямоугольные координаты Локальные системы плоских прямоугольных координат применяют на небольших по площади участках. Систему образуют две
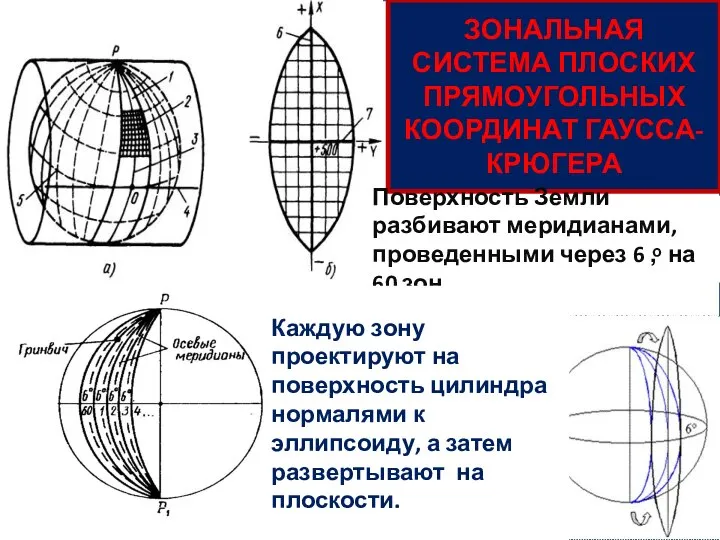
- 11. ЗОНАЛЬНАЯ СИСТЕМА ПЛОСКИХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ГАУССА-КРЮГЕРА Поверхность Земли разбивают меридианами, проведенными через 6 ,ͦ на 60
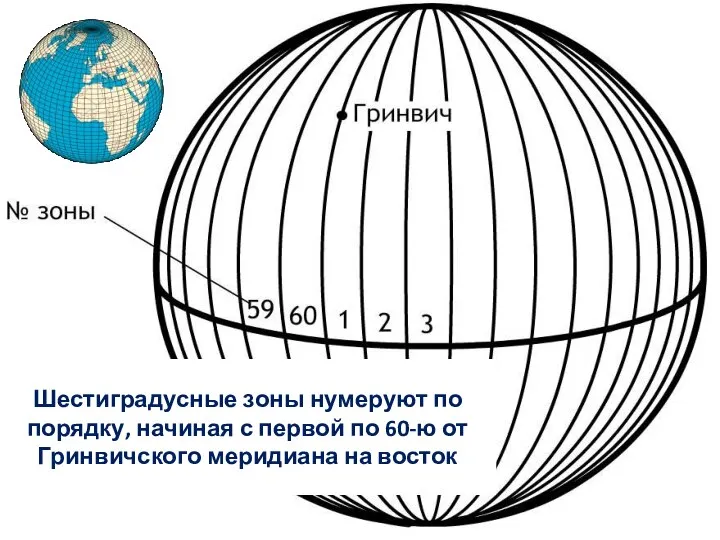
- 12. Шестиградусные зоны нумеруют по порядку, начиная с первой по 60-ю от Гринвичского меридиана на восток
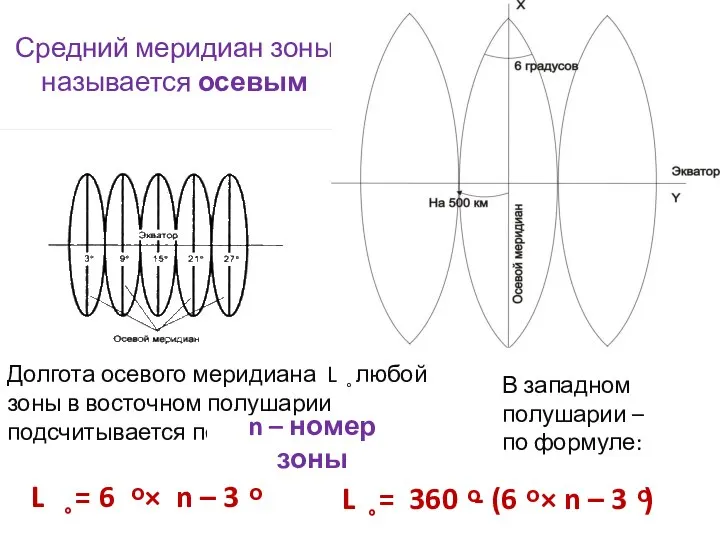
- 13. Средний меридиан зоны называется осевым L ̥ = 6 ͦ × n – 3 ͦ Долгота
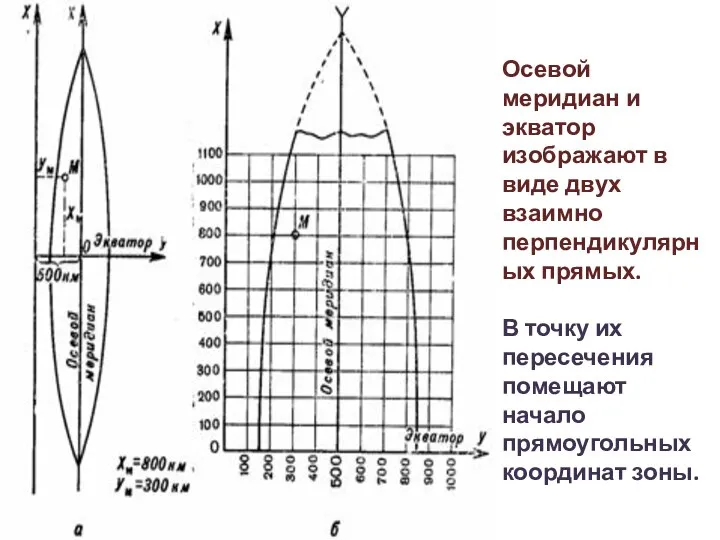
- 14. Осевой меридиан и экватор изображают в виде двух взаимно перпендикулярных прямых. В точку их пересечения помещают
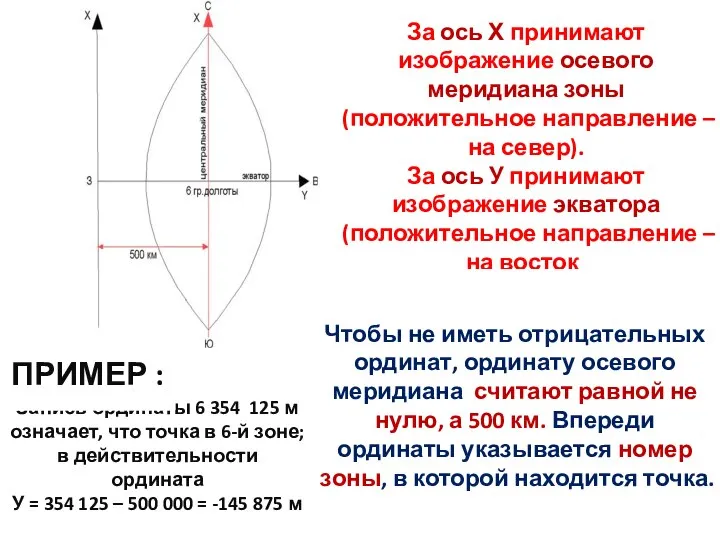
- 15. За ось Х принимают изображение осевого меридиана зоны (положительное направление – на север). За ось У
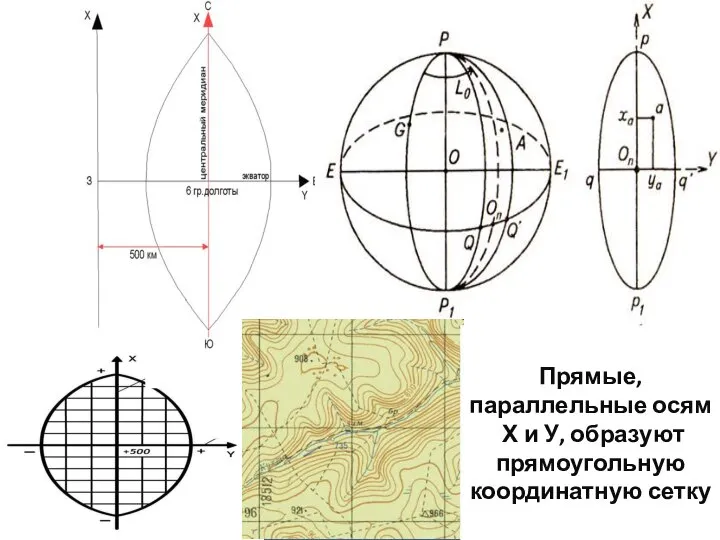
- 16. Прямые, параллельные осям Х и У, образуют прямоугольную координатную сетку
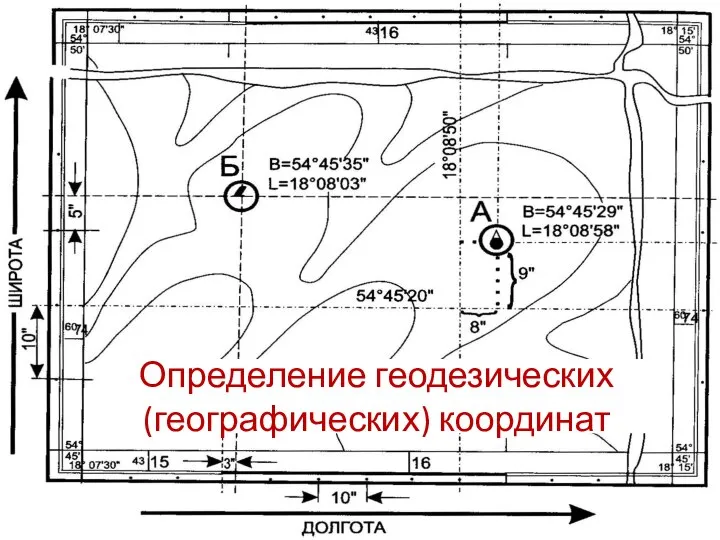
- 19. Определение геодезических (географических) координат
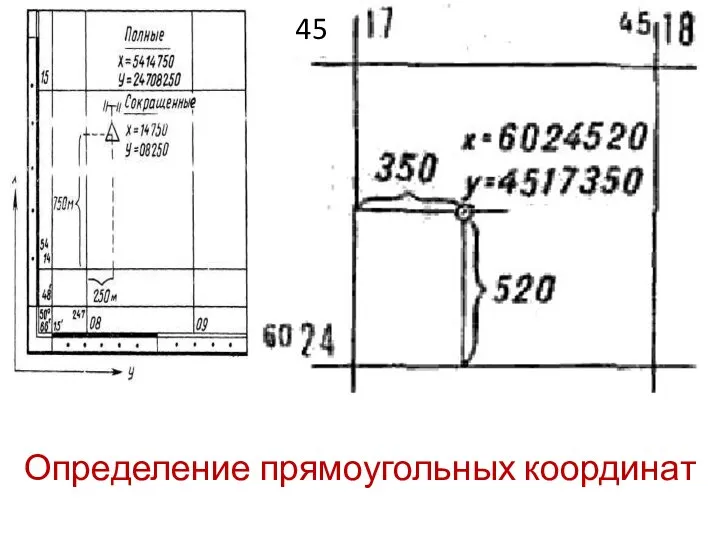
- 20. 5 45 Определение прямоугольных координат
- 21. ОРИЕНТИРОВАНИЕ ЛИНИЙ
- 22. Ориентировать линию – значит определить ее направление относительно другого направления, принятого за начальное. В геодезии за
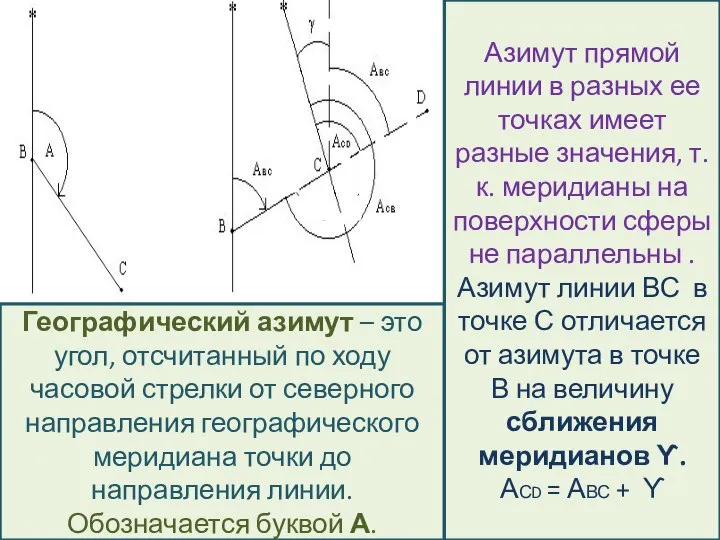
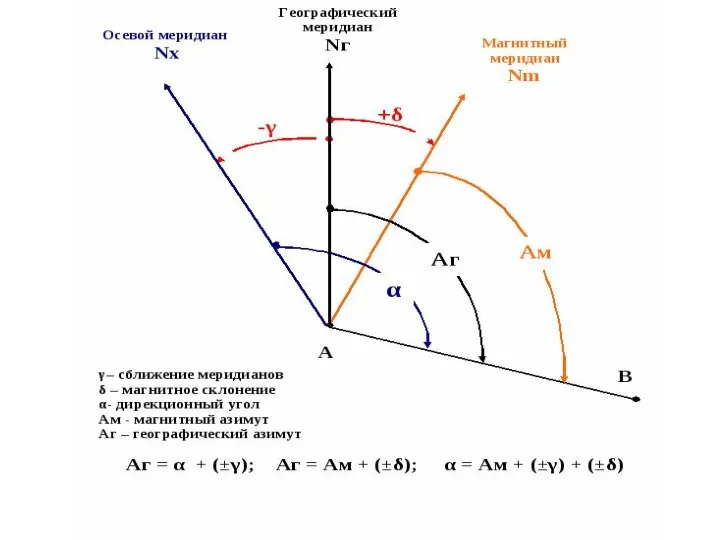
- 23. Географический азимут – это угол, отсчитанный по ходу часовой стрелки от северного направления географического меридиана точки
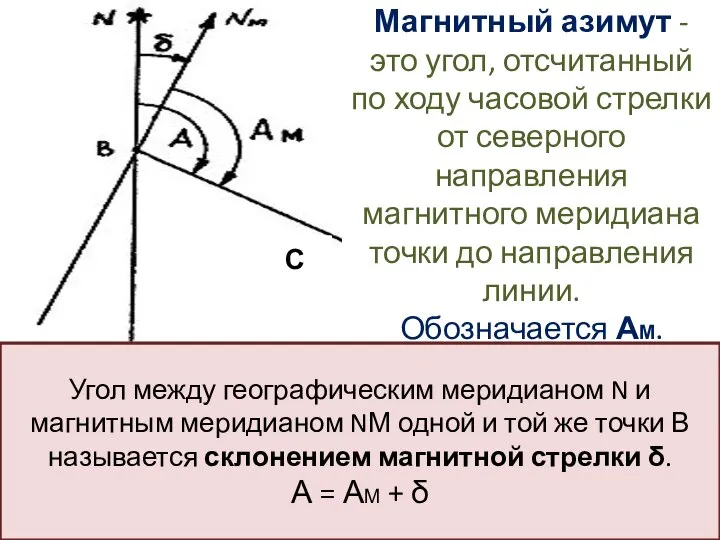
- 24. С Магнитный азимут - это угол, отсчитанный по ходу часовой стрелки от северного направления магнитного меридиана
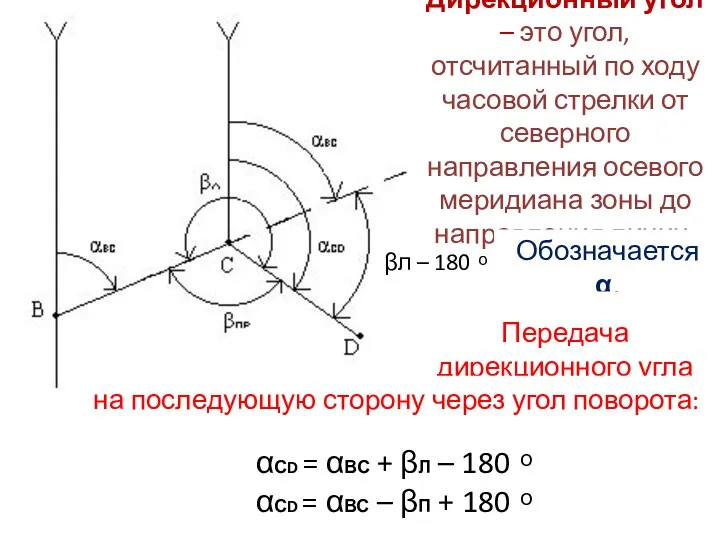
- 25. βл – 180 ͦ Дирекционный угол – это угол, отсчитанный по ходу часовой стрелки от северного
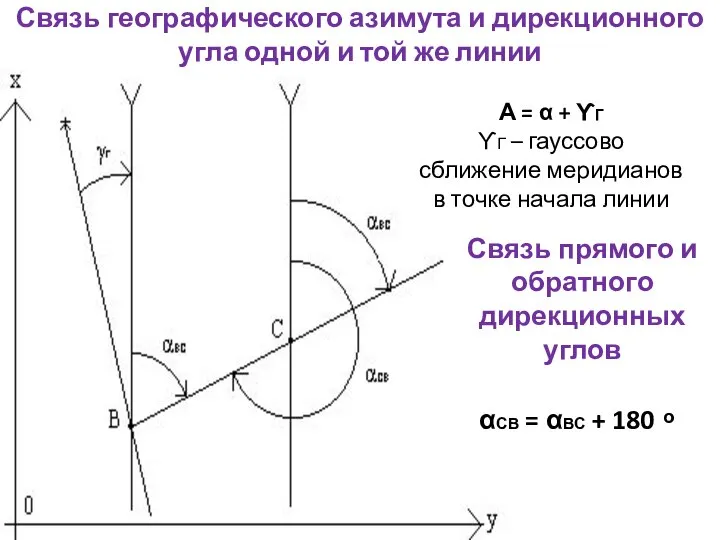
- 26. Связь географического азимута и дирекционного угла одной и той же линии А = α + ϒГ
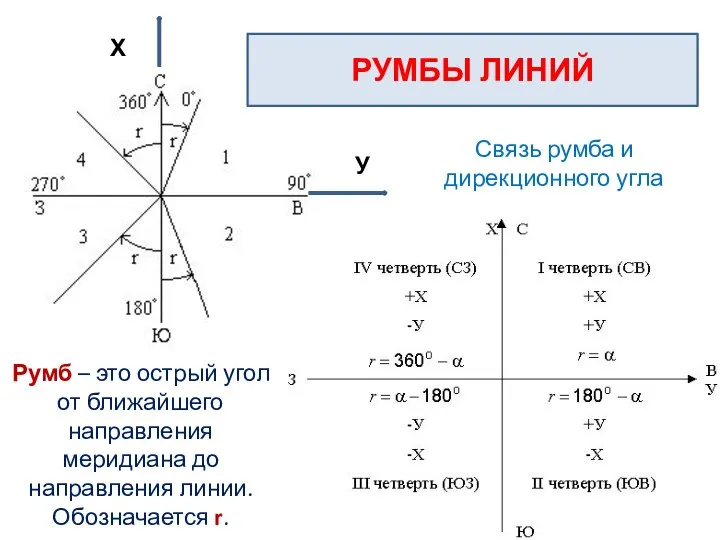
- 28. У Х РУМБЫ ЛИНИЙ Связь румба и дирекционного угла Румб – это острый угол от ближайшего
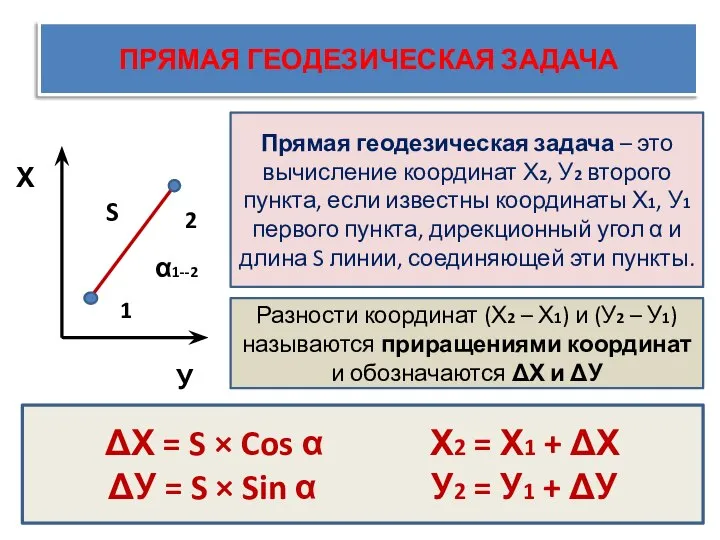
- 29. ПРЯМАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА Х У 1 2 Прямая геодезическая задача – это вычисление координат Х2, У2
- 30. ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА Обратная геодезическая задача – это вычисление дирекционного угла α и длины S линии,
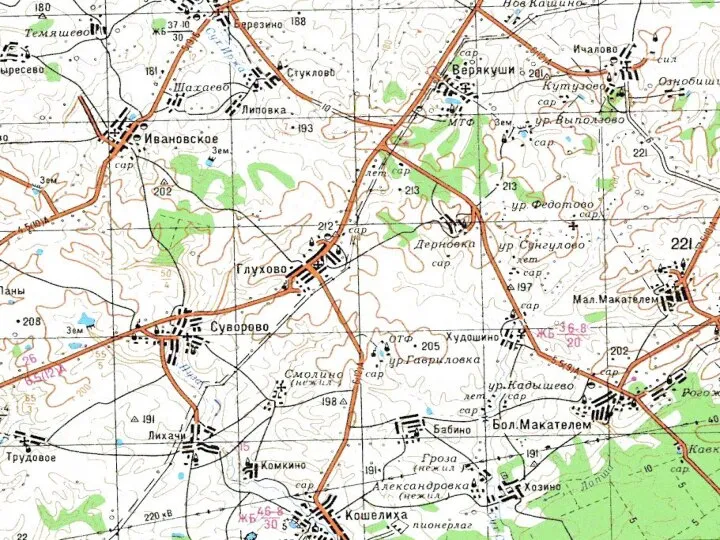
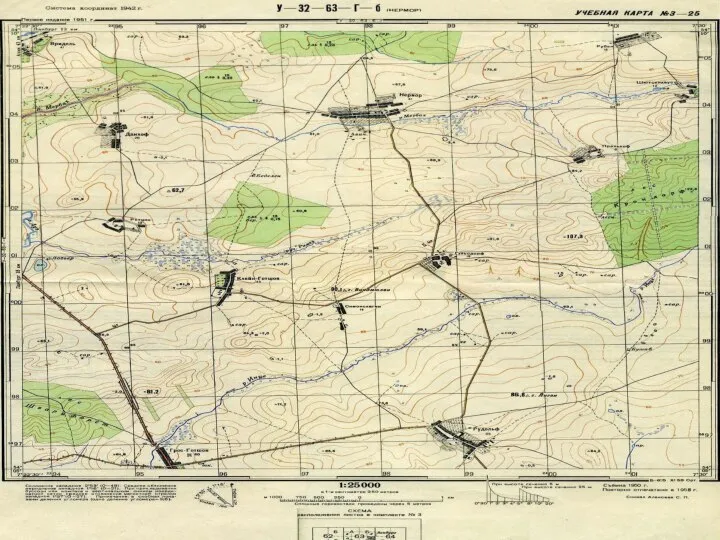
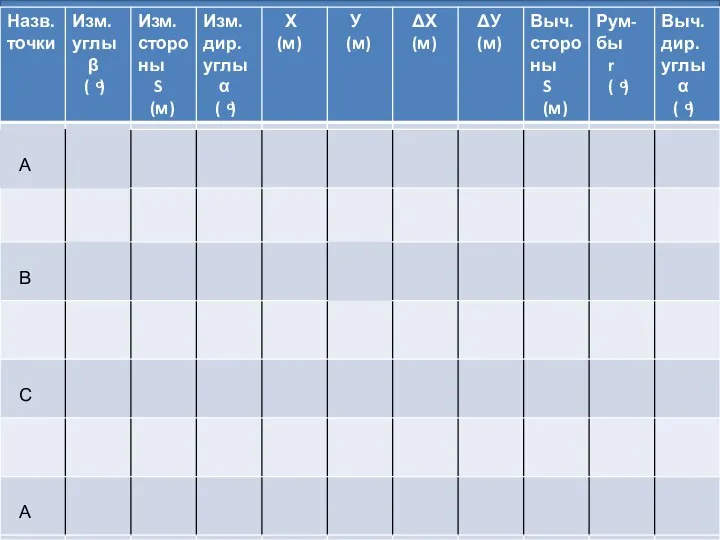
- 31. РАБОТА №4 РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКОЙ КАРТЕ Цель работы: изучение топографической карты (плана), определение координат, ориентирных
- 33. Контрольные вопросы Какие координаты относятся к сферическим, а какие – к плоским? Что называется широтой и
- 35. Скачать презентацию








 Санатории и здравницы полуострова Крым
Санатории и здравницы полуострова Крым Яно-Индигирский экологический район
Яно-Индигирский экологический район Водные богатства
Водные богатства География средних и высших учебных заведений г. Новосибирска
География средних и высших учебных заведений г. Новосибирска Переверзев Владимир 11-а класс Возникновение христианства
Переверзев Владимир 11-а класс Возникновение христианства Natural places
Natural places Путешествие по планете Земля
Путешествие по планете Земля Презентация на тему Тундра
Презентация на тему Тундра 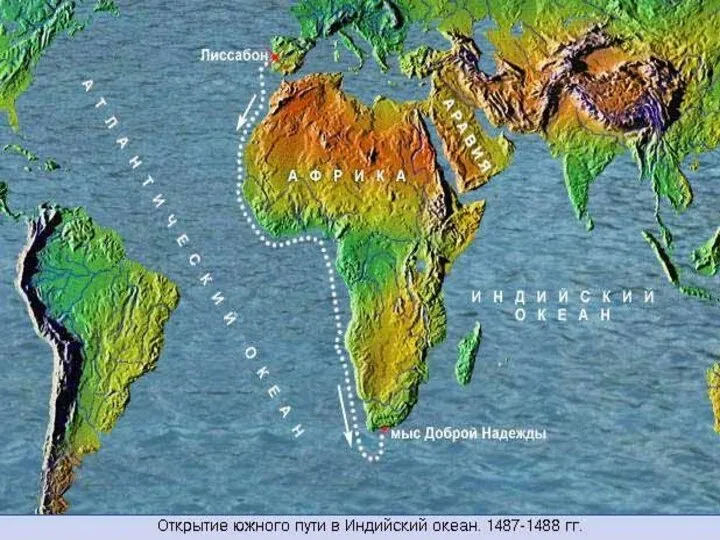 Африка. Открытие морского пути в Индию. 1497-1499 гг
Африка. Открытие морского пути в Индию. 1497-1499 гг Музей Седова
Музей Седова Экскурсия по Австралии
Экскурсия по Австралии Презентация на тему Каспийское море
Презентация на тему Каспийское море  Открытие Америки. 5 кл
Открытие Америки. 5 кл 20141009_dvizhenie_vod_mirovogo_okeana
20141009_dvizhenie_vod_mirovogo_okeana Природные комплексы суши и океана
Природные комплексы суши и океана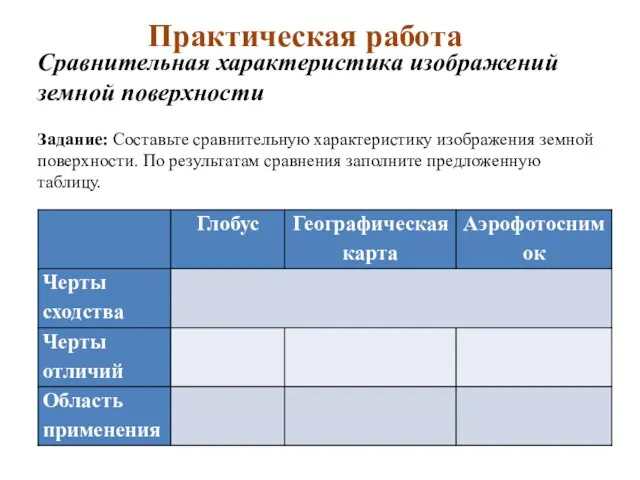 Сравнительная характеристика изображений земной поверхности. Шаблон
Сравнительная характеристика изображений земной поверхности. Шаблон Сравнительная характеристика песков аллювия р. Москвы
Сравнительная характеристика песков аллювия р. Москвы Исследование болота моего села
Исследование болота моего села Материк Австралия. Тест
Материк Австралия. Тест Пустыня
Пустыня Ответьте на вопросы: С какими изменениями условий среды связаны оцепенение и спячка у животных? Для каких животных характерна спя
Ответьте на вопросы: С какими изменениями условий среды связаны оцепенение и спячка у животных? Для каких животных характерна спя Породы-коллекторы 1
Породы-коллекторы 1 Зарубежная Европа
Зарубежная Европа Презентация на тему Достопримечательности Канады
Презентация на тему Достопримечательности Канады  Муссонный климат
Муссонный климат Население Африки
Население Африки Формы рельефа земного шара на контурной карте
Формы рельефа земного шара на контурной карте Мексика
Мексика