Содержание
- 2. Моделирование Задачи моделирования: планирование съемки; подавление кратных волн; привязка скважинных данных к наземной сейсморазведке; оценка качества
- 3. Лучевое трассирование Постановка задачи Дано: S (sx , sy , sz) – координаты источника ?⃗ -
- 4. Шаг №1. Уравнение поверхности отражателя 1) а11х2 + а22у2 + а33z2 + 2а12xy + 2а13xz +
- 5. Шаг №2. Длина пути пробега от S до P P = S + L x I
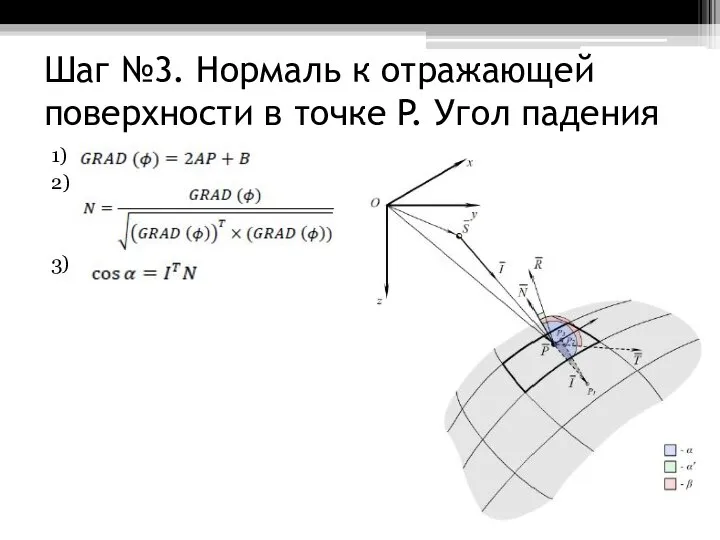
- 6. Шаг №3. Нормаль к отражающей поверхности в точке P. Угол падения 1) 2) 3)
- 7. Шаг №4. Уравнение проходящего и отраженного лучей 1) 2) 3) 4) 5) 6)
- 8. Шаг №3.Случай слоя с непрерывным изменением скорости 1) 2) 3) 4) 5) 6) 7)
- 9. Лучевое трассирование Итог: сейсмотрасса - с увеличением сложности среды возникает проблема нелинейности решения обратной задачи -
- 10. Конечно-разностный метод: схема Лебедева, Вирье, RSGS Введем некую равномерную сетку с целыми и полуцелыми узлами, как
- 11. Конечно-разностное моделирование + позволяет использовать модель-решетку любой сложности и дает качественный результат - требует значительных вычислительных
- 12. Конечно-объемный метод WENO/Рунге-Кутта Разбиваем плоскость на ячейки потоки Интегрируем по объему ячейки Аппроксимация N-точечной квадратурной формулой
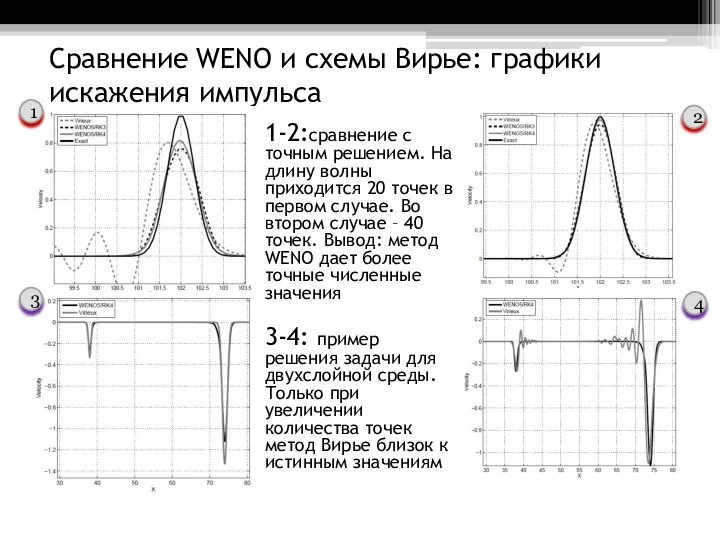
- 13. Сравнение WENO и схемы Вирье: графики искажения импульса 1-2:сравнение с точным решением. На длину волны приходится
- 14. Вопросы Способы моделирования Какие схемы используются при конечно-разностном моделировании? Какой метод самый быстрый? Какой наиболее точный?
- 16. Скачать презентацию











 Исследование образа жизни населения России и Республики Калмыкия
Исследование образа жизни населения России и Республики Калмыкия Цивилизации Востока (общие черты)
Цивилизации Востока (общие черты) Нелегальный туризм
Нелегальный туризм Глобус и карта
Глобус и карта Соединённые Штаты Америки (США)
Соединённые Штаты Америки (США) Презентация на тему Географические Карты
Презентация на тему Географические Карты  Игра Интелектуалия
Игра Интелектуалия Япония. Географическое положение
Япония. Географическое положение Нефтегазовая гидрогеология. Лекция 6. Гидрогеологические условия миграции, аккумуляции, консервации и деструкции нефти и газа
Нефтегазовая гидрогеология. Лекция 6. Гидрогеологические условия миграции, аккумуляции, консервации и деструкции нефти и газа Презентация на тему Растения саванны и редколесья Африки (8 класс)
Презентация на тему Растения саванны и редколесья Африки (8 класс)  Города России
Города России Инвестиционные карты пилотных регионов
Инвестиционные карты пилотных регионов Определение климатического пояса г. Иваново
Определение климатического пояса г. Иваново Не исчезай моя деревня!. Вязьевская (Чернецовская) волость
Не исчезай моя деревня!. Вязьевская (Чернецовская) волость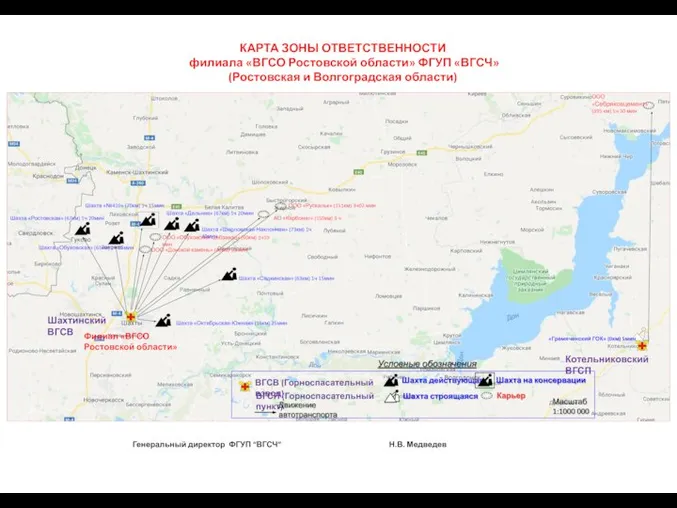 Карта зоны ответственности ВГСО РО
Карта зоны ответственности ВГСО РО Тайга. Баргузинский и Лазовский заповедники
Тайга. Баргузинский и Лазовский заповедники Китай. Индия. Япония
Китай. Индия. Япония Геологическое летоисчисление и геологическая карта
Геологическое летоисчисление и геологическая карта Виды интеграции
Виды интеграции Презентация на тему Все о Японии
Презентация на тему Все о Японии  Таиланд
Таиланд Обитатели пустыни бедуины
Обитатели пустыни бедуины Sayasi-karta
Sayasi-karta Презентация на тему Человек и земная кора
Презентация на тему Человек и земная кора  Презентация на тему Город Ярославль
Презентация на тему Город Ярославль  Антарктида с вопросами
Антарктида с вопросами Город золотого кольца России Иваново
Город золотого кольца России Иваново Осень
Осень