Содержание
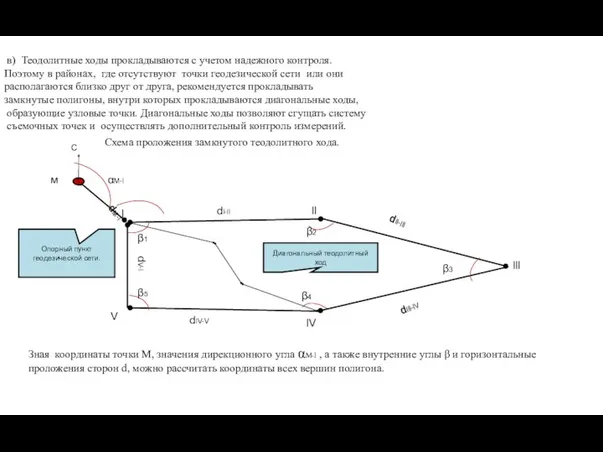
- 2. Схема проложения замкнутого теодолитного хода. l ll lll lV V Опорный пункт геодезической сети. С м
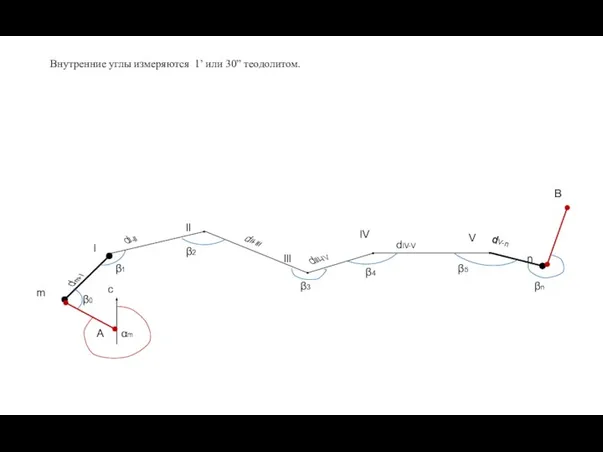
- 4. dV-n Внутренние углы измеряются 1’ или 30” теодолитом.
- 5. СЪЕМКА ПОДРОБНОСТЕЙ. Производится с пунктов теодолитного хода в соответствии с заданием и масштабом плана и определяет
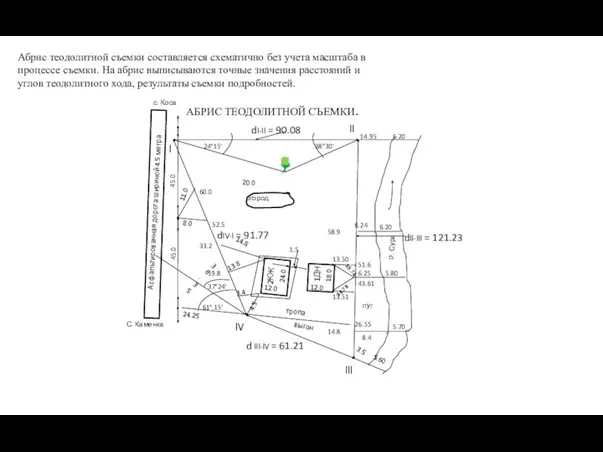
- 6. Абрис теодолитной съемки составляется схематично без учета масштаба в процессе съемки. На абрис выписываются точные значения
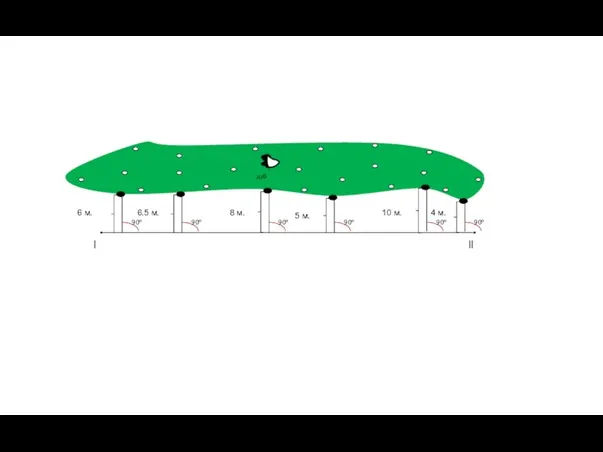
- 7. дуб l ll 6 м. 6.5 м. 8 м. 5 м. 10 м. 4 м.
- 8. Способ створов. Способ створов применяется в тех случаях когда определяемая точка, находится на продолжении линии теодолитного
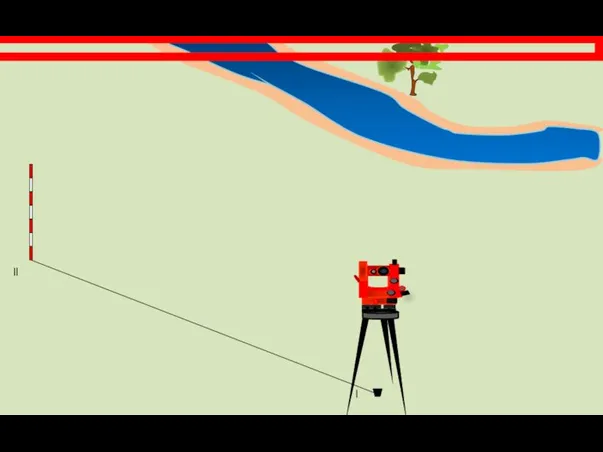
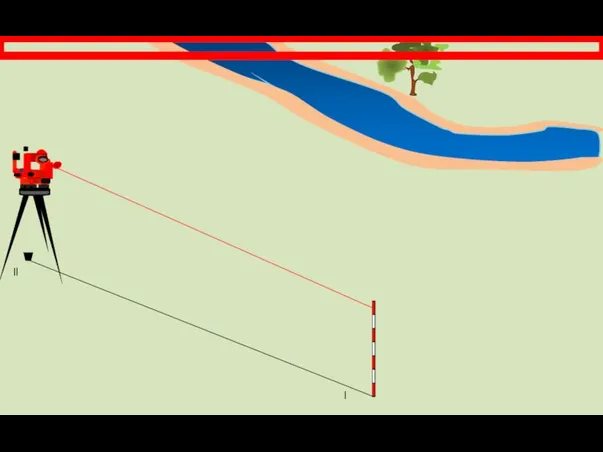
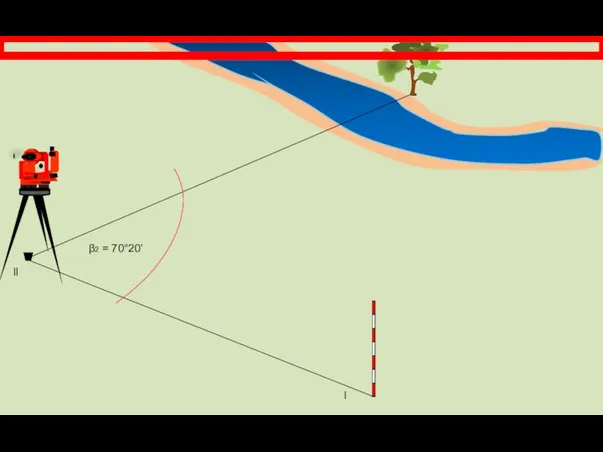
- 9. Способ угловых засечек. Наиболее выгодно применять этот способ при определении положения точек, расположенных в труднодоступных местах.
- 10. l ll
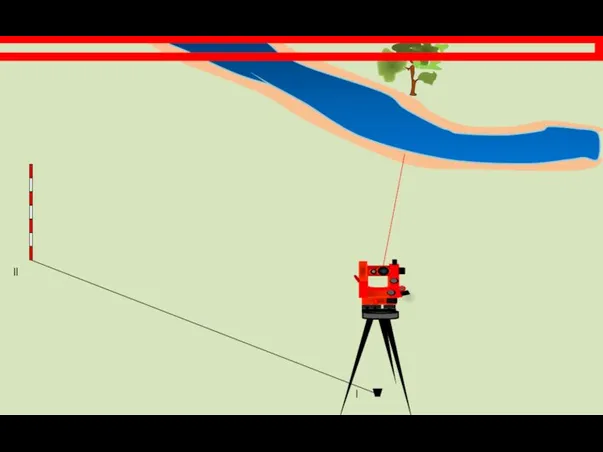
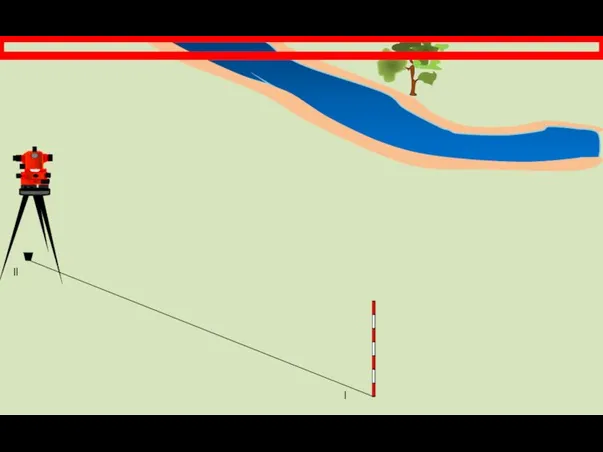
- 11. ll
- 12. l ll
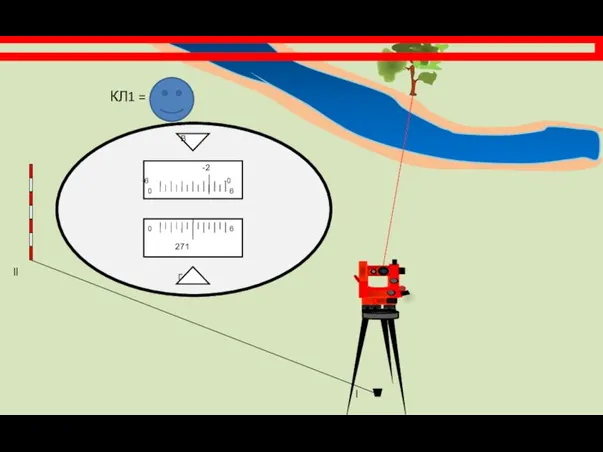
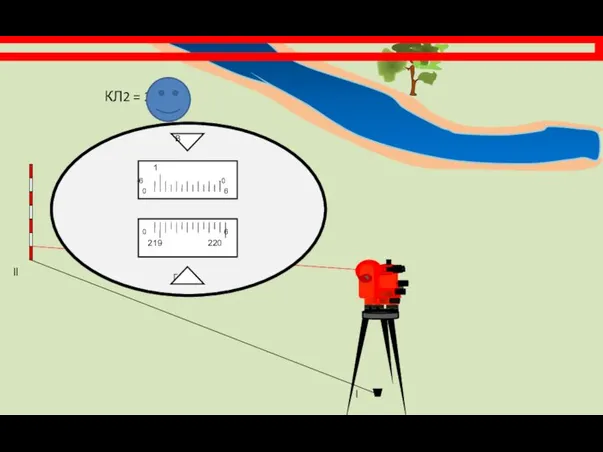
- 13. Затем теодолит переводится на вешку установленную на точке ll и берется отсчет КЛ2.
- 14. l ll
- 15. l ll
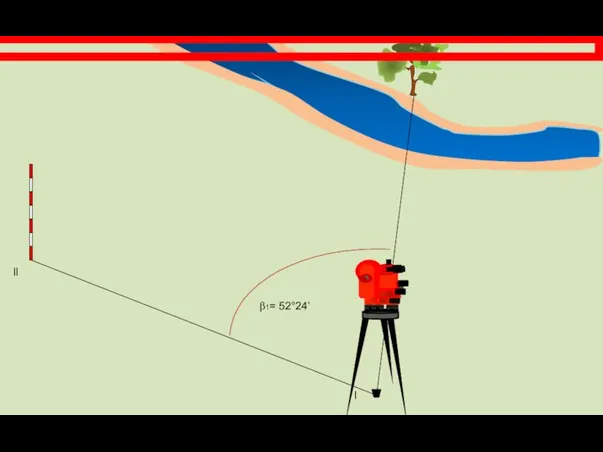
- 16. Угол β1 = КЛ2 – КЛ1 = 271°29’ – 219°05’ = 52°24’ Переносим теодолит в точку
- 17. l ll β1= 52°24’
- 18. l ll
- 19. l ll
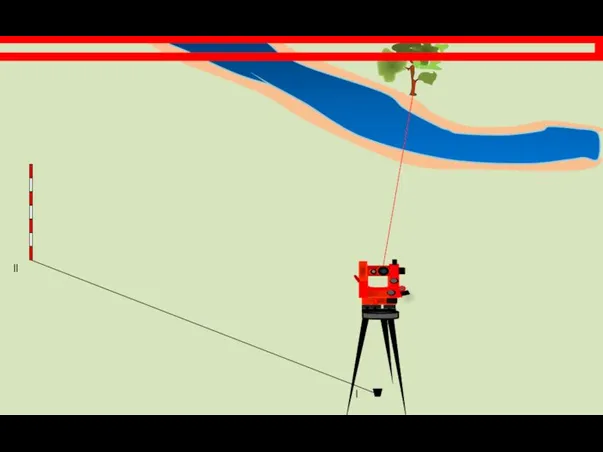
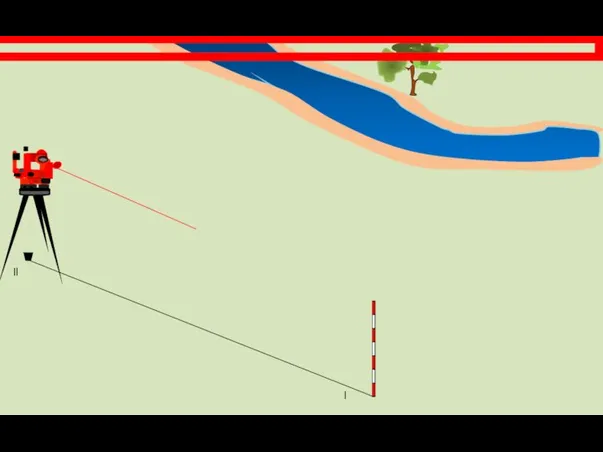
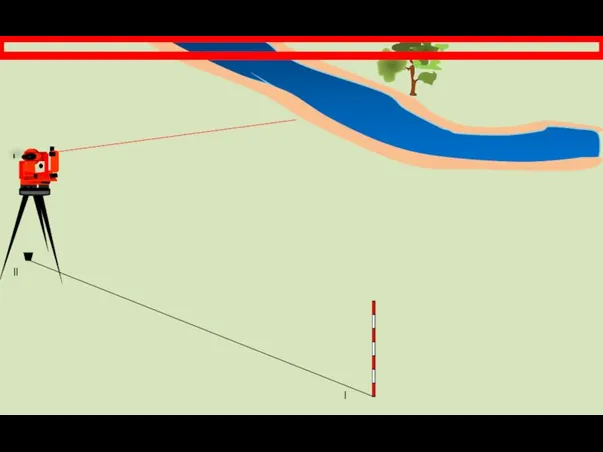
- 20. Переводим трубу теодолита на дерево и берем отсчет КЛ2.
- 21. l ll
- 22. l ll
- 23. l ll
- 24. l ll
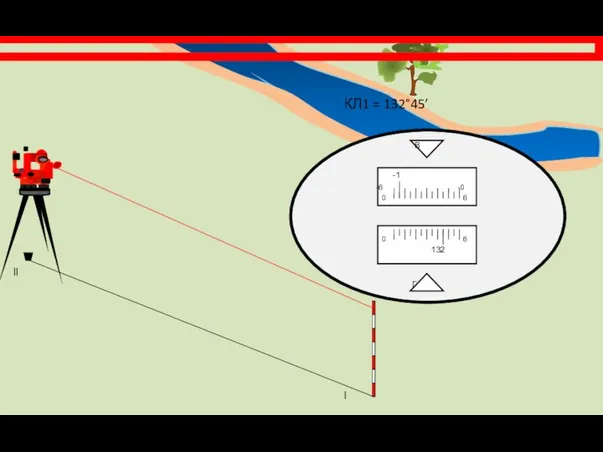
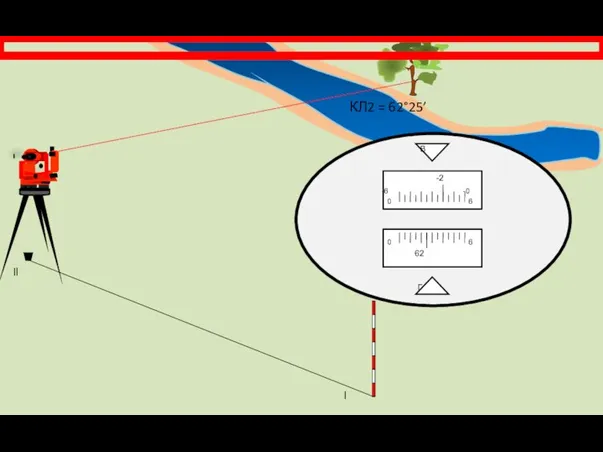
- 25. Угол β2 = КЛ1 – КЛ2 = 132°45’ – 62°25’ = 70°20’ Угол засечки равен 180°
- 26. l ll β2 = 70°20’
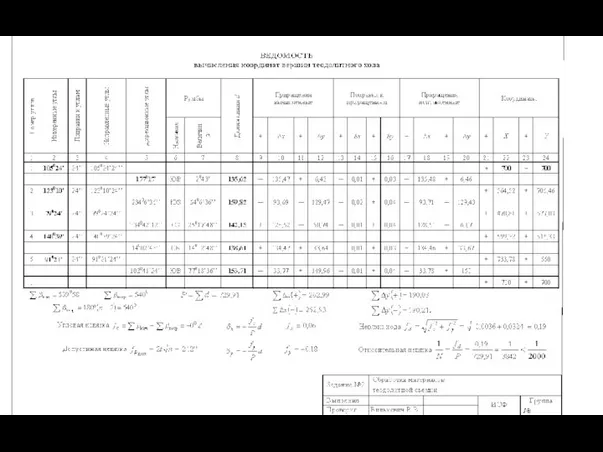
- 28. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ПРИ ТЕОДОЛИТНОЙ СЪЕМКЕ. Камеральная обработка результатов съемки заключается в выполнении вычислительных и графических
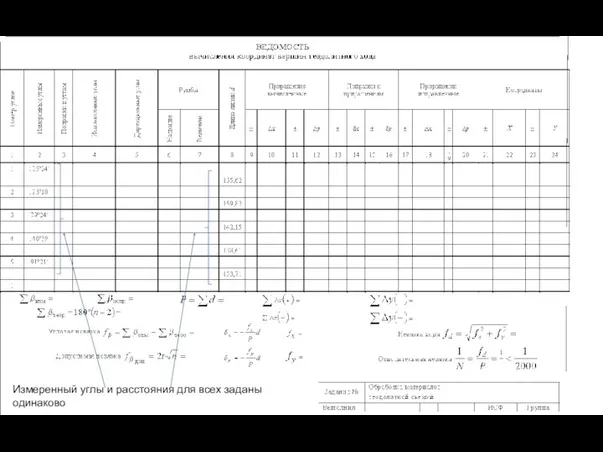
- 29. Измеренный углы и расстояния для всех заданы одинаково
- 30. f = Σβ пр – Σβ теор. В процессе камеральной обработки устанавливается соответствие результатов измерений, требованиям
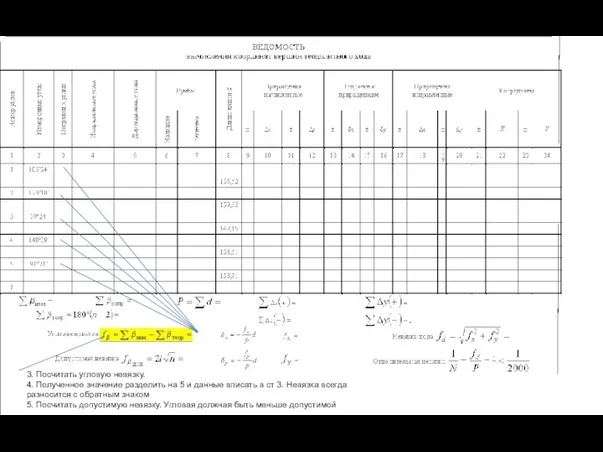
- 31. ОБРАБОТКА УГЛОВЫХ ИЗМЕРЕНИЙ. Практические измерения углов сопровождаются ошибками. Величиной точности теодолитного хода является угловая невязка, которая
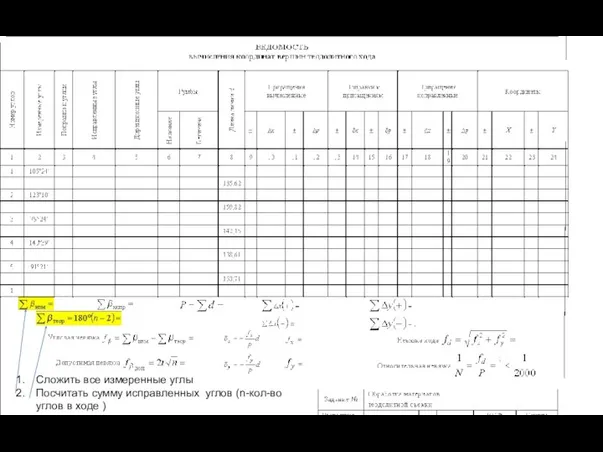
- 32. Сложить все измеренные углы Посчитать сумму исправленных углов (n-кол-во углов в ходе )
- 33. 3. Посчитать угловую невязку. 4. Полученное значение разделить на 5 и данные вписать в ст 3.
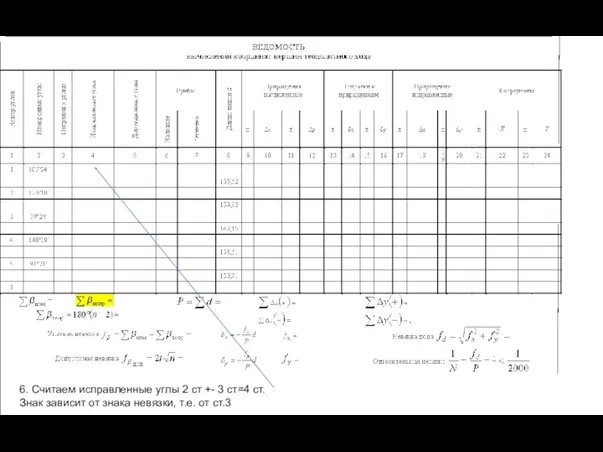
- 34. 6. Считаем исправленные углы 2 ст +- 3 ст=4 ст. Знак зависит от знака невязки, т.е.
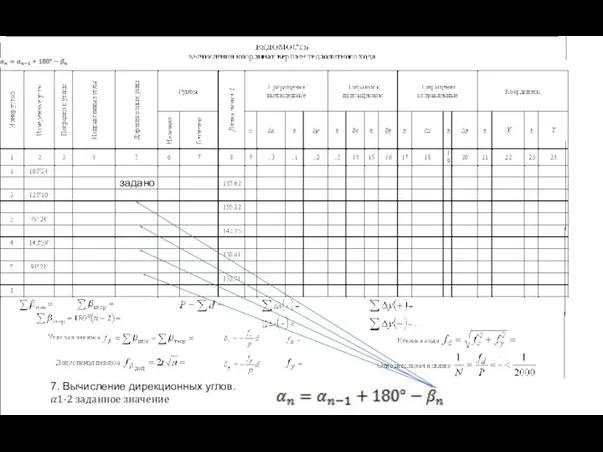
- 35. 7. Вычисление дирекционных углов. ?1-2 заданное значение задано
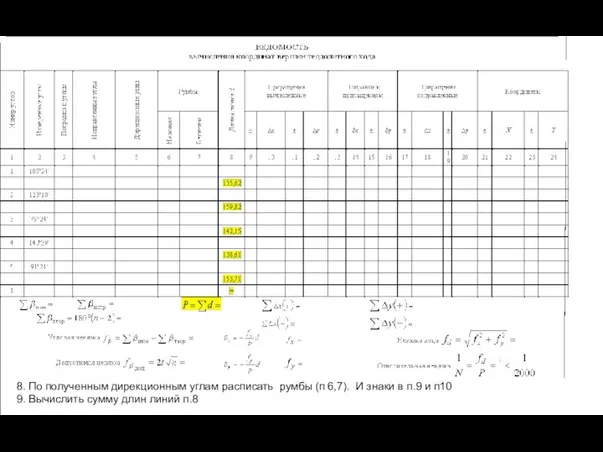
- 36. 8. По полученным дирекционным углам расписать румбы (п 6,7). И знаки в п.9 и п10 9.
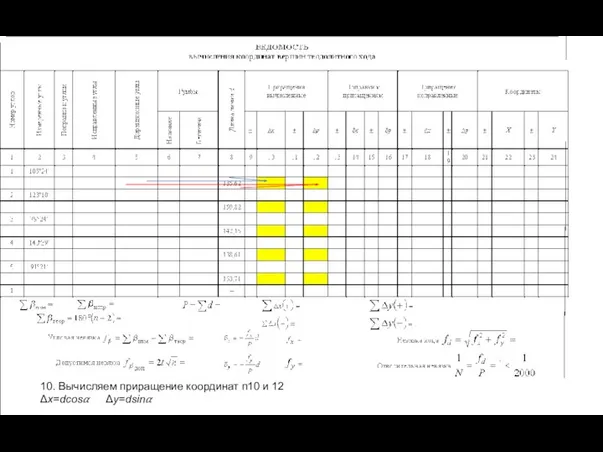
- 37. 10. Вычисляем приращение координат п10 и 12 Δx=dcos? Δy=dsin?
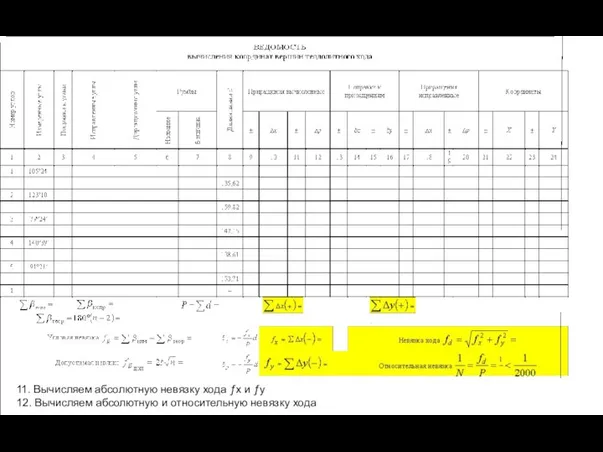
- 38. 11. Вычисляем абсолютную невязку хода ƒx и ƒy 12. Вычисляем абсолютную и относительную невязку хода
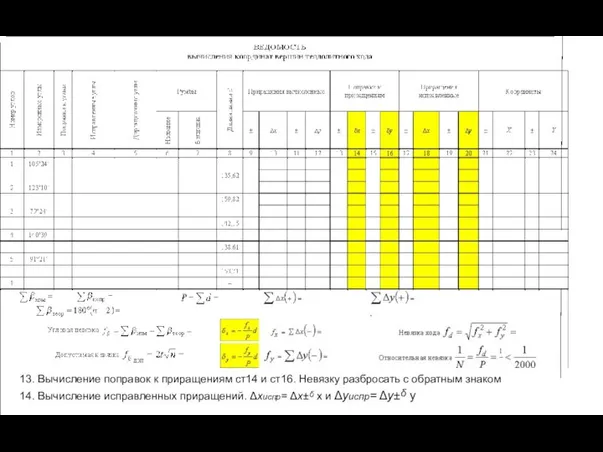
- 39. 13. Вычисление поправок к приращениям ст14 и ст16. Невязку разбросать с обратным знаком 14. Вычисление исправленных
- 40. Вычисление координат вершин теодолитного хода п 22 и 24. Хпосл. = Х пред. + ΔХиспр. ;
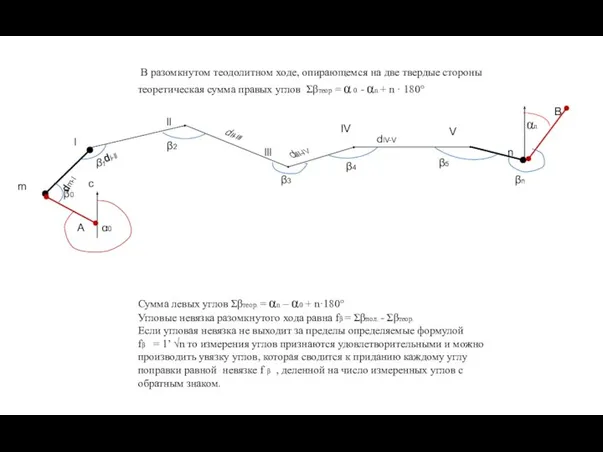
- 41. В разомкнутом теодолитном ходе, опирающемся на две твердые стороны теоретическая сумма правых углов Σβтеор = α
- 42. ВЫЧИСЛЕНИЕ КООРДИНАТ ЗАМКНУТОГО ТЕОДОЛИТНОГО ХОДА. Вычисление координат замкнутого теодолитного хода подробно рассмотрено в презентации « Построение
- 43. ВЫЧИСЛЕНИЕ КООРДИНАТ ДИАГОНАЛЬНОГО ХОДА. Вычисление координат диагонального хода производится в следующей последовательности. 1.Вычисляется сумма измеренных углов.
- 44. 11. Определяем относительную невязку хода по формуле: ƒотн. = ƒр / Р, для удобства сравнения относительную
- 45. ПОСТРОЕНИЕ ПЛАНА ТЕОДОЛИТНОЙ СЪЕМКИ. Построение плана теодолитной съемки подробно рассматривается на лабораторных занятиях, а также подробно
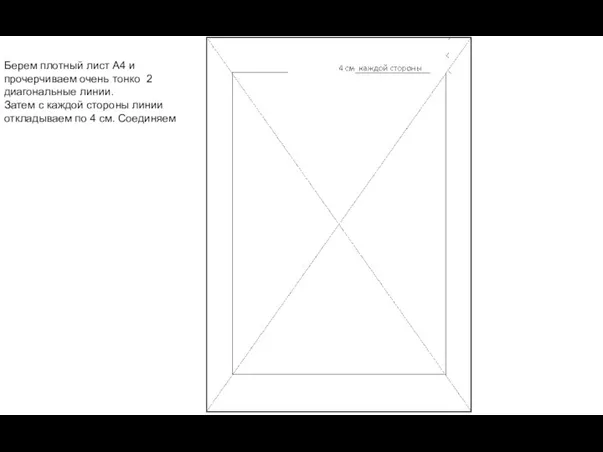
- 46. Берем плотный лист А4 и прочерчиваем очень тонко 2 диагональные линии. Затем с каждой стороны линии
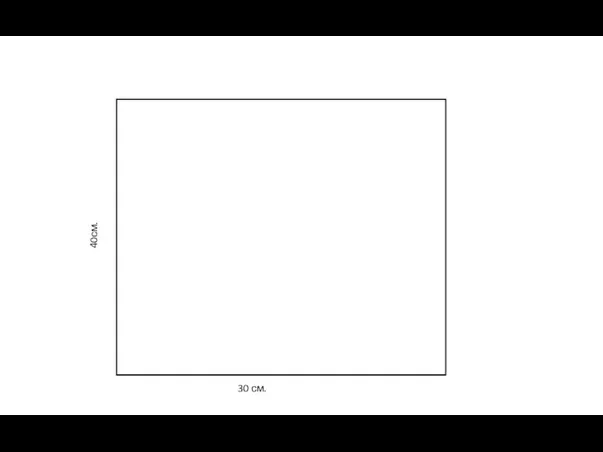
- 47. 30 см. 40см.
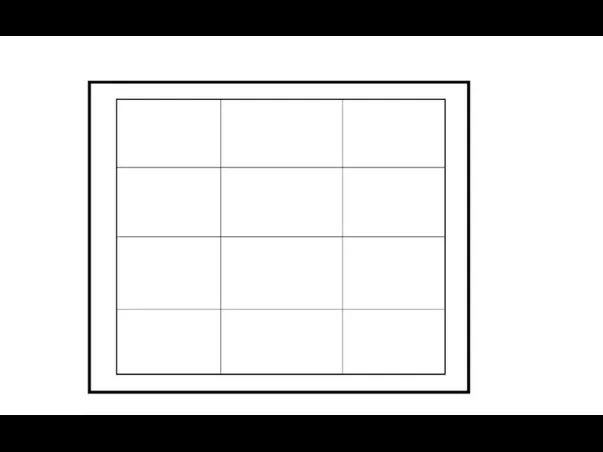
- 48. Вокруг первой рамки, на расстоянии 1 см от ее края, строим вторую, с толщиной линии 2
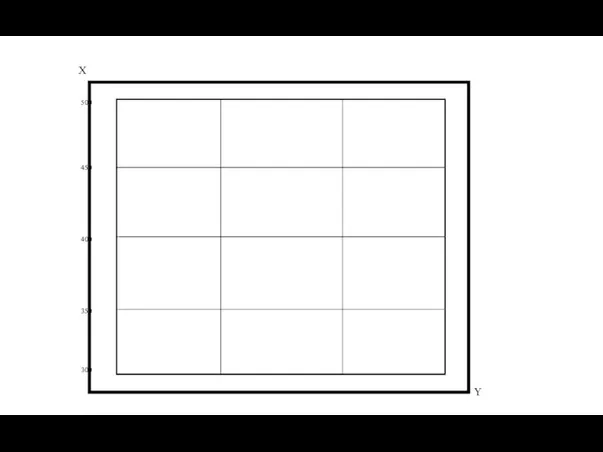
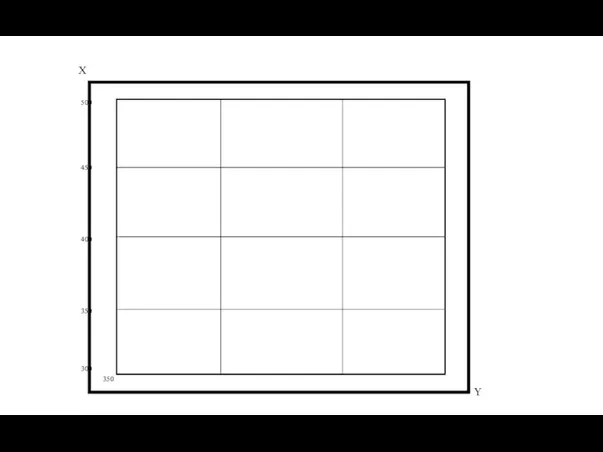
- 50. Оцифровка координатной сетки. Оцифровка координатной сетки производится следующим образом: а. Из координатной ведомости выбираются точки с
- 51. X Y 300 Производим оцифровку по оси Х через 50 метров.
- 52. X Y 300 500 450 400 350
- 53. Выбираем наименьшую координату по оси Y, Такой координатой является 379.93. Начинаем оцифровку через 50 метров с
- 54. X Y 300 500 450 400 350 350
- 55. X Y 300 500 450 400 350 350 400 450 500 350 400 450 500 500
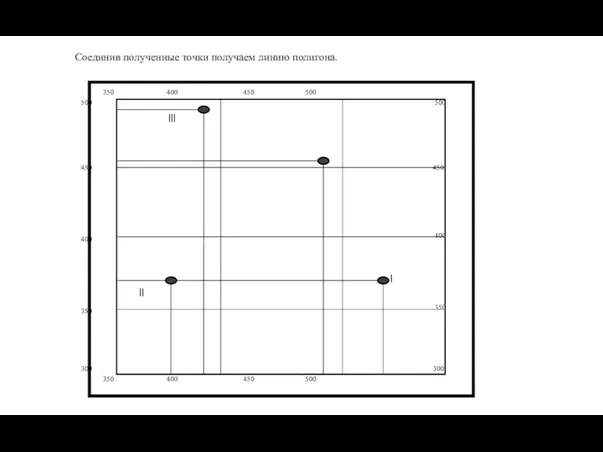
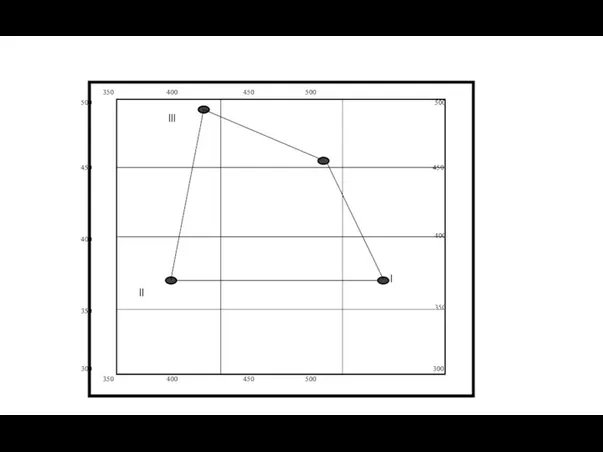
- 56. Из координатной ведомости, выносим точки по их координатам, на координатную сетку.
- 57. 300 500 450 400 350 350 400 450 500 350 400 450 500 500 450 400
- 58. 300 500 450 400 350 350 400 450 500 350 400 450 500 500 450 400
- 60. Скачать презентацию






















 Карта Иркутска
Карта Иркутска Volcanic eruption
Volcanic eruption Воды Антарктиды
Воды Антарктиды Обобщение данных о температуре воздуха по ЯНАО
Обобщение данных о температуре воздуха по ЯНАО Пресноводное озеро Виви
Пресноводное озеро Виви Узнай больше о Крыме
Узнай больше о Крыме Практическая работа № 2. Описание океана и моря по плану на основе анализа географических карт
Практическая работа № 2. Описание океана и моря по плану на основе анализа географических карт Світовий океан
Світовий океан Ost-Berlin
Ost-Berlin Кочёвский муниципальный округ
Кочёвский муниципальный округ Озеро Развал
Озеро Развал Технология разработки мерзлого и скального грунта
Технология разработки мерзлого и скального грунта Презентация на тему Изображение рельефа на планах и картах
Презентация на тему Изображение рельефа на планах и картах  Великие географические открытия
Великие географические открытия Экскурсия по городу Снежинску
Экскурсия по городу Снежинску Движения земной коры
Движения земной коры Global warming
Global warming Обобщающий урок по теме: Земля. Своя игра
Обобщающий урок по теме: Земля. Своя игра Ландшафтоведение как раздел физической географии, объект и предмет изучения
Ландшафтоведение как раздел физической географии, объект и предмет изучения Презентация на тему Голландия
Презентация на тему Голландия  Особо охраняемые природные территории
Особо охраняемые природные территории Мой удивительный край - Красноборск
Мой удивительный край - Красноборск 20141113_chasti_mirovogo_okeana
20141113_chasti_mirovogo_okeana Презентация на тему Иллюстрация движения воды в океане
Презентация на тему Иллюстрация движения воды в океане  Проверим знания и умения ориентироваться в природе
Проверим знания и умения ориентироваться в природе Презентация на тему Водяной пар. Влажность воздуха
Презентация на тему Водяной пар. Влажность воздуха  География лк
География лк Расовый и этнический состав населения
Расовый и этнический состав населения