Содержание
- 2. 26.1.2. Ортодромия и ее элементы Ортодромия – дуга большого круга (ДБК) – кратчайшее расстояние между двумя
- 3. Элементы дуги большого круга – ортодромии Исходная (начальная) точка ортодромии → т. А (φА λА или
- 4. 26.2. Основные формулы ортодромии. Способы ее задания 26.2.1. Основные формулы ортодромии Сферический треугольник ортодромии Из сферической
- 6. Скачать презентацию
Слайд 226.1.2. Ортодромия и ее элементы
Ортодромия – дуга большого круга (ДБК) – кратчайшее
26.1.2. Ортодромия и ее элементы
Ортодромия – дуга большого круга (ДБК) – кратчайшее
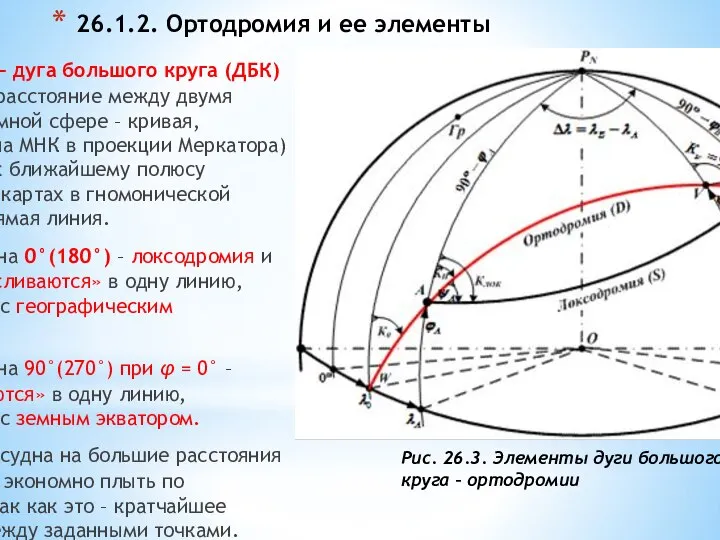
При курсе судна 0°(180°) – локсодромия и ортодромия «сливаются» в одну линию, совпадающую с географическим меридианом.
При курсе судна 90°(270°) при φ = 0° – также «сливаются» в одну линию, совпадающую с земным экватором.
При плавании судна на большие расстояния (тысячи миль) экономно плыть по ортодромии, так как это – кратчайшее расстояние между заданными точками.
Рис. 26.3. Элементы дуги большого круга – ортодромии
Слайд 3Элементы дуги большого круга – ортодромии
Исходная (начальная) точка ортодромии → т. А
Элементы дуги большого круга – ортодромии
Исходная (начальная) точка ортодромии → т. А
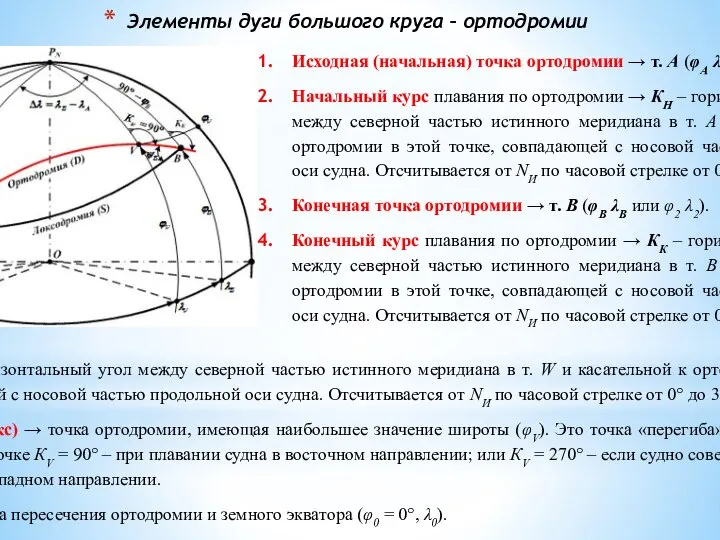
Начальный курс плавания по ортодромии → КН – горизонтальный угол между северной частью истинного меридиана в т. А и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.
Конечная точка ортодромии → т. В (φВ λВ или φ2 λ2).
Конечный курс плавания по ортодромии → КК – горизонтальный угол между северной частью истинного меридиана в т. В и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.
5. Курс К0 → горизонтальный угол между северной частью истинного меридиана в т. W и касательной к ортодромии в этой точке, совпадающей с носовой частью продольной оси судна. Отсчитывается от NИ по часовой стрелке от 0° до 360°.
6. Точка V (вертекс) → точка ортодромии, имеющая наибольшее значение широты (φV). Это точка «перегиба» ортодромии и курс судна в этой точке КV = 90° – при плавании судна в восточном направлении; или КV = 270° – если судно совершает плавание по ортодромии в западном направлении.
7. Точка W → точка пересечения ортодромии и земного экватора (φ0 = 0°, λ0).
Слайд 426.2. Основные формулы ортодромии. Способы ее задания
26.2.1. Основные формулы ортодромии
Сферический треугольник ортодромии
Из
26.2. Основные формулы ортодромии. Способы ее задания
26.2.1. Основные формулы ортодромии
Сферический треугольник ортодромии
Из

Применяя формулу «косинуса стороны» («…косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…») можно определить длину ортодромии (D) между любыми двумя ее точками (т. А и т. В), координаты которых известны, то есть:
cosD = cos(90° − φA) · cos(90° − φB) + sin(90° − φA) · sin(90° − φB) · cos(λB – λA)
 Игра по географии Географическая мозаика
Игра по географии Географическая мозаика Презентация на тему Цунами
Презентация на тему Цунами  Парки и скверы города Магнитогорска. Часть 1
Парки и скверы города Магнитогорска. Часть 1 Сценарий этнографического праздника на территории Столинского района на базе заказников Средняя припять и Ольманские болота
Сценарий этнографического праздника на территории Столинского района на базе заказников Средняя припять и Ольманские болота Япония
Япония ПОЛЕЗНЫЕ ИСКОПАЕМЫЕ
ПОЛЕЗНЫЕ ИСКОПАЕМЫЕ Приземная карта погоды
Приземная карта погоды Презентация на тему Формирование политической карты мира
Презентация на тему Формирование политической карты мира  Географический рисунок расселения и хозяйства
Географический рисунок расселения и хозяйства Мой город
Мой город Коренные народы и народности России
Коренные народы и народности России 20140111_orientirovanie4
20140111_orientirovanie4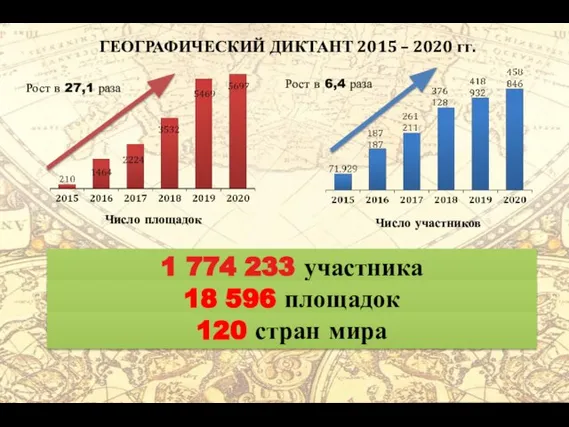 Географический диктант 2015 – 2020 гг
Географический диктант 2015 – 2020 гг Республика Ирландия
Республика Ирландия Почва. 6 класс
Почва. 6 класс Информационные материалы по температуре на территории Республики Крым
Информационные материалы по температуре на территории Республики Крым Республика Казахстан
Республика Казахстан Западная Сибирь
Западная Сибирь История формирования рельефа Земли
История формирования рельефа Земли Презентация на тему Алтай
Презентация на тему Алтай  Презентация на тему ПК России УРАЛ
Презентация на тему ПК России УРАЛ  Великие географические открытия
Великие географические открытия Восемь удивительных мест за два дня
Восемь удивительных мест за два дня ИсторияМинСырья-1
ИсторияМинСырья-1 Реки. Речная система
Реки. Речная система Русская равнина. Урок-игра
Русская равнина. Урок-игра Характеристика реки
Характеристика реки Мировой океан и его проблемы
Мировой океан и его проблемы