Содержание
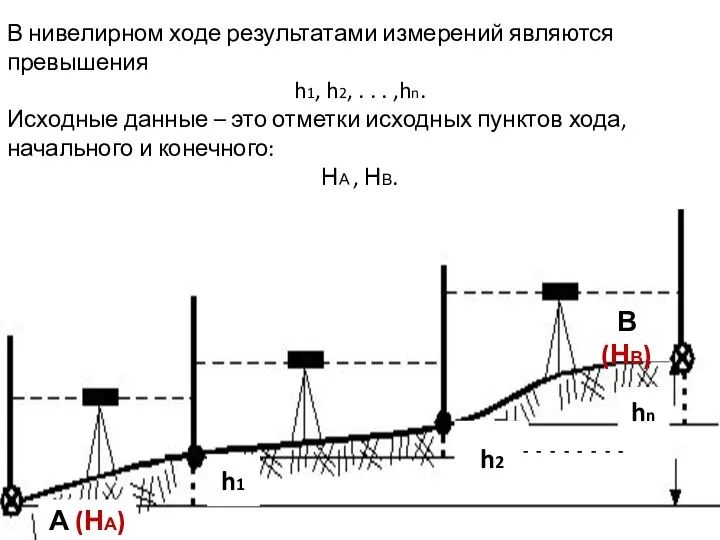
- 2. А (НА) В (НВ) h1 h2 hn - - - - - - - - В
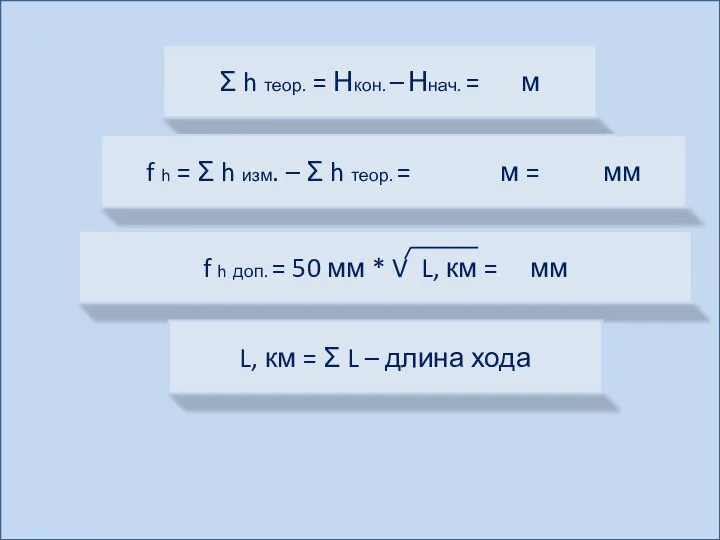
- 3. Если бы измеренные превышения точно соответствовали своим истинным (теоретическим) значениям, то выполнялось бы следующее геометрическое условие:
- 4. Уравнивание – это математическая обработка измерений с целью ликвидации невязки В измерения вводят поправки V так,
- 5. Чтобы вычислить отметки определяемых пунктов хода, нужно к предыдущей отметке прибавить уравненное превышение между соответствующими точками:
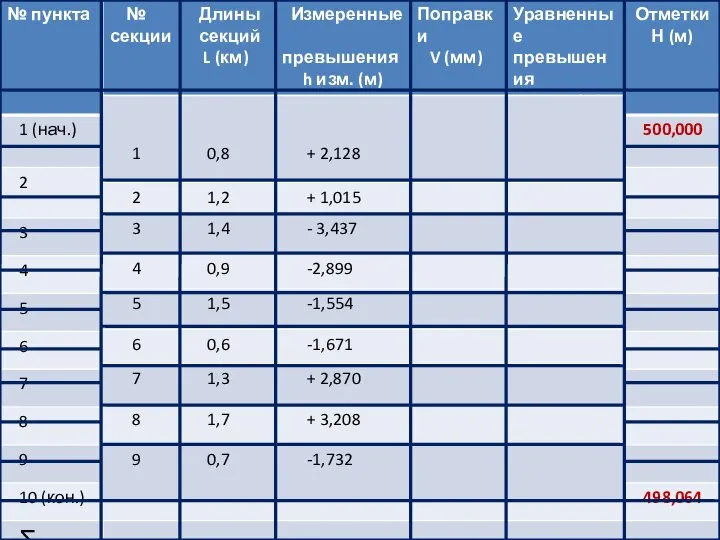
- 6. Работа № 3 УРАВНИВАНИЕ НИВЕЛИРНОГО ХОДА Цель работы: выполнить математическую обработку измерений в нивелирном ходе. Содержание
- 8. Σ h теор. = Нкон. – Ннач. = м f h = Σ h изм. –
- 10. Скачать презентацию




 1_ Преобразование рельефа в результате хозяйственн
1_ Преобразование рельефа в результате хозяйственн Таиланд
Таиланд Город Ярославль
Город Ярославль London Traffic
London Traffic Флора и фауна. 7 класс
Флора и фауна. 7 класс Нұр-Сұлтан жағалауы
Нұр-Сұлтан жағалауы Презентация на тему Украина в символах (6 класс)
Презентация на тему Украина в символах (6 класс)  Географический брейн-ринг Наш дом - планета Земля
Географический брейн-ринг Наш дом - планета Земля Неблагоприятные климатические явления
Неблагоприятные климатические явления Германия. Западная Европа
Германия. Западная Европа Рассказ о родном городе Докучаевск. Назовите памятное место города или название улицы по фотографии
Рассказ о родном городе Докучаевск. Назовите памятное место города или название улицы по фотографии 20161207_prezentatsiya_microsoft_reki_yu.a
20161207_prezentatsiya_microsoft_reki_yu.a Презентация на тему Часовые зоны России
Презентация на тему Часовые зоны России  Бишкек шаары
Бишкек шаары Формы земной поверхности
Формы земной поверхности Виче́нца — город в итальянской области
Виче́нца — город в итальянской области Водні маси. 7 клас
Водні маси. 7 клас Воздух. Его особенности. 3 класс
Воздух. Его особенности. 3 класс Деревня моя Ёгна
Деревня моя Ёгна Хабаровск. 5 площадка
Хабаровск. 5 площадка 7кл_Рельеф Земли_
7кл_Рельеф Земли_ Метаморфизм нефти
Метаморфизм нефти Безлесные природные зоны России
Безлесные природные зоны России Презентация на тему Коста-Рика
Презентация на тему Коста-Рика 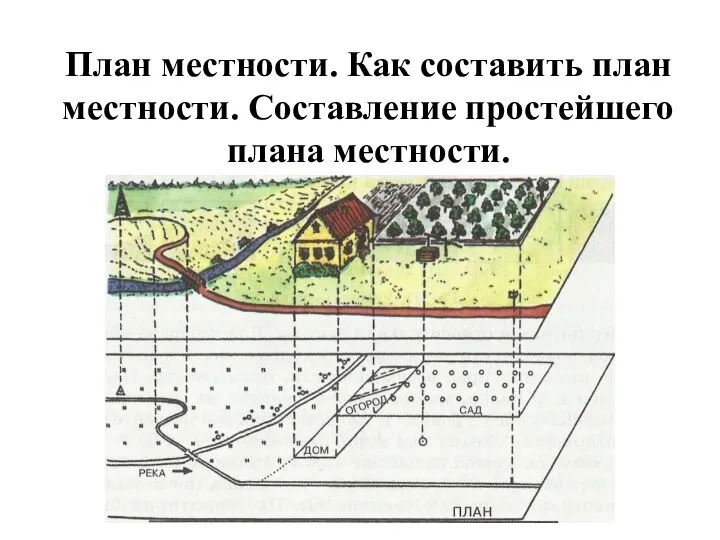 План местности. Составление простейшего плана местности
План местности. Составление простейшего плана местности Государство Испания
Государство Испания Улицы нашего города Набережные Челны
Улицы нашего города Набережные Челны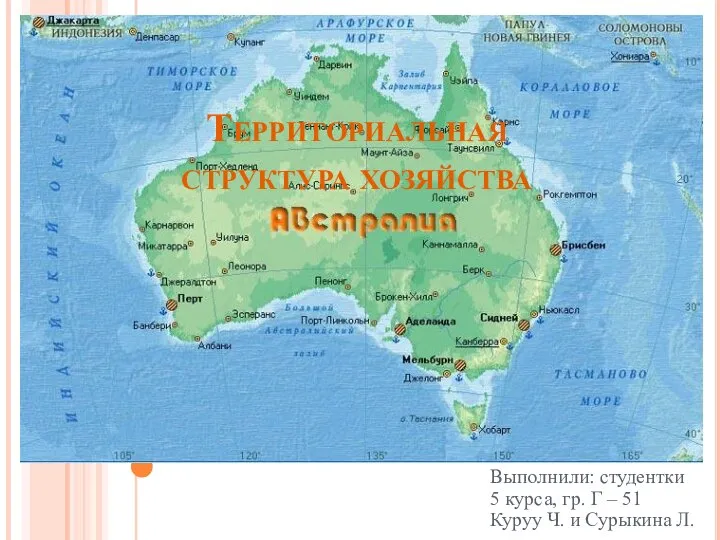 Территориальная структура хозяйства
Территориальная структура хозяйства