Содержание
- 2. Цель лекции Целью лекции является приобретение теоретических знаний в области алгоритмизации и программирования
- 3. План Понятие алгоритма и его свойства Способы описания алгоритмов Основные алгоритмические конструкции Базовые алгоритмы
- 4. 1. Понятие алгоритма и его свойства Алгоритм (от algoritmi)- предписание, однозначно задающее процесс преобразования исходной информации
- 5. Разновидности алгоритмов: вычислительные – работают с простыми видами данных (числа, векторы, матрицы), но процесс вычисления может
- 6. Свойства алгоритма Дискретность – последовательное выполнение простых или ранее определённых (подпрограммы) шагов. Преобразование исходных данных в
- 7. Составление алгоритма является обязательным этапом автоматизации любого процесса.
- 8. 2. Способы описания алгоритмов словесный (на естественном языке); формульно-словесный; табличный (обычно носит вспомогательный характер); графический (использует
- 9. Блок-схема - графическое изображение структуры алгоритма, в котором каждый этап процесса переработки данных представляется в виде
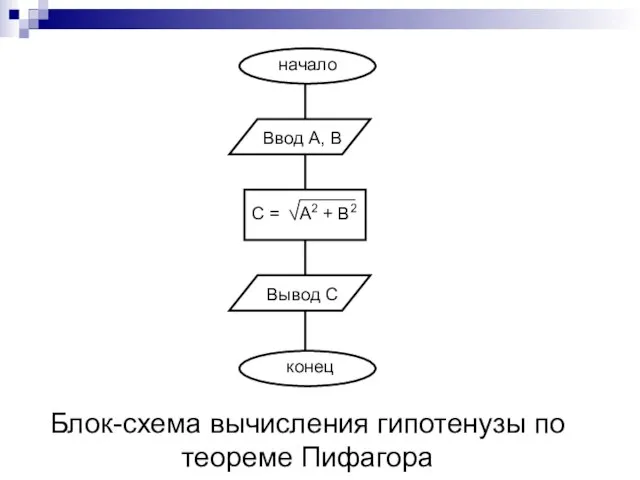
- 11. 3. Основные алгоритмические конструкции Линейным принято называть вычислительный процесс, в котором этапы вычислений выполняются в линейной
- 12. Блок-схема вычисления гипотенузы по теореме Пифагора
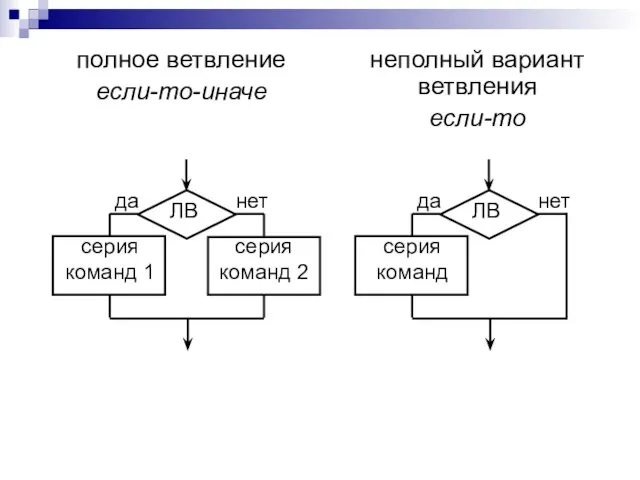
- 13. Разветвляющийся вычислительный процесс реализуется по одному из нескольких заранее предусмотренных направлений (ветвей) в зависимости от выполнения
- 14. полное ветвление если-то-иначе неполный вариант ветвления если-то
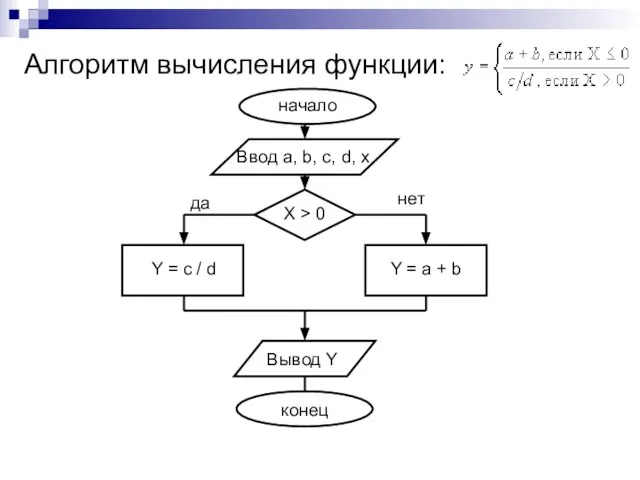
- 15. Алгоритм вычисления функции:
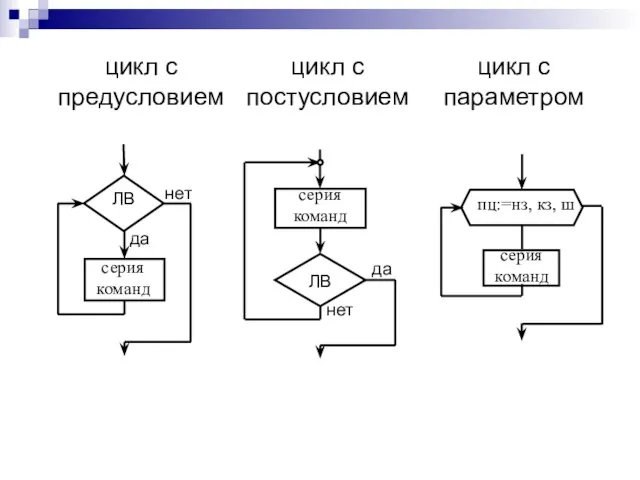
- 16. Циклический вычислительный процесс (цикл) включает участки, на которых вычисления выполняются многократно по одним и тем же
- 17. Цикл называется детерминированным (цикл с параметром), если число повторений тела цикла заранее известно или определено. Цикл
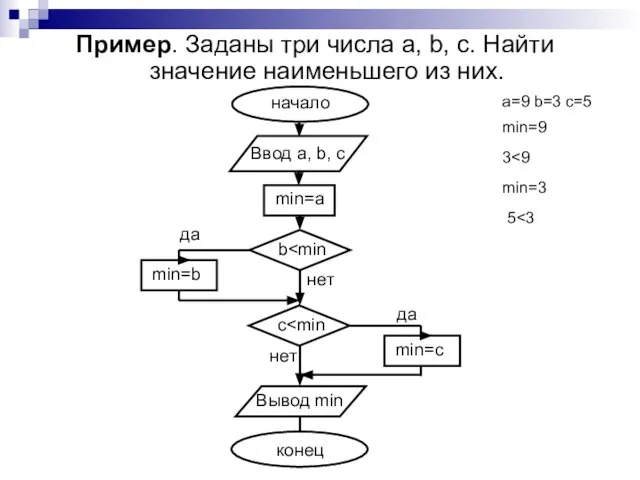
- 19. 4. Базовые алгоритмы Алгоритм поиска наибольшего (наименьшего) значения: за max (min) принимаем значение любого из данных
- 20. Пример. Заданы три числа a, b, c. Найти значение наименьшего из них. a=9 b=3 c=5 min=9
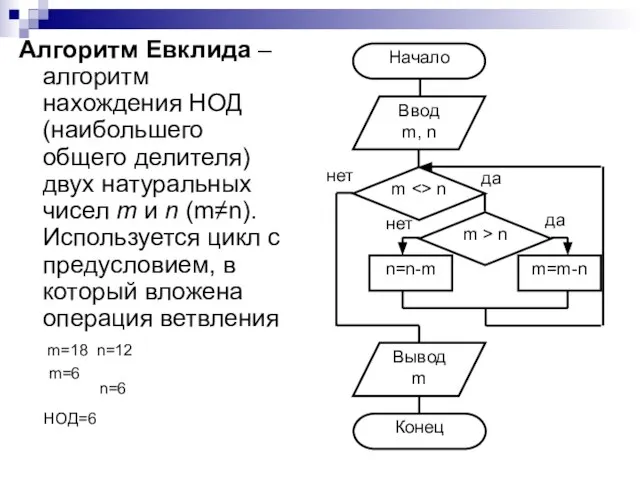
- 21. Алгоритм Евклида – алгоритм нахождения НОД (наибольшего общего делителя) двух натуральных чисел m и n (m≠n).
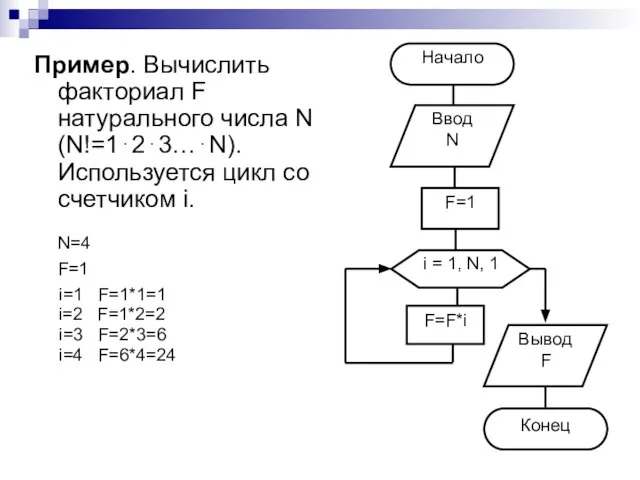
- 22. Пример. Вычислить факториал F натурального числа N (N!=1⋅2⋅3…⋅N). Используется цикл со счетчиком i. N=4 F=1 i=1
- 23. Правило произведения: начальное значение произведения Р=1; в теле некоторой циклической конструкции выполнить команду: Р = Р
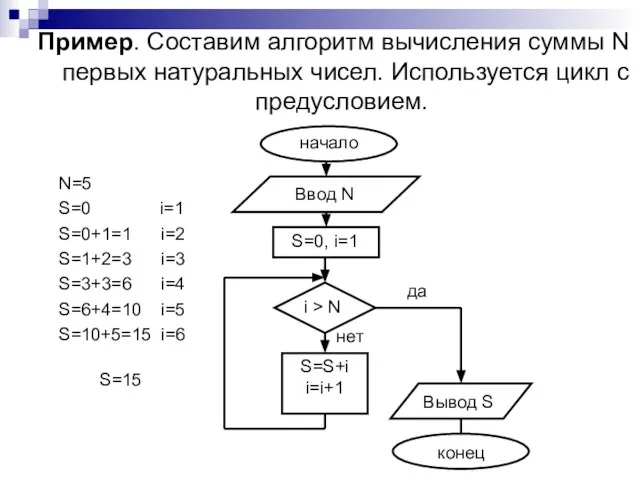
- 24. Пример. Составим алгоритм вычисления суммы N первых натуральных чисел. Используется цикл с предусловием. N=5 S=0 i=1
- 25. Правило суммирования: начальное значение суммы S=0; в теле некоторой циклической конструкции выполнить команду: S = S
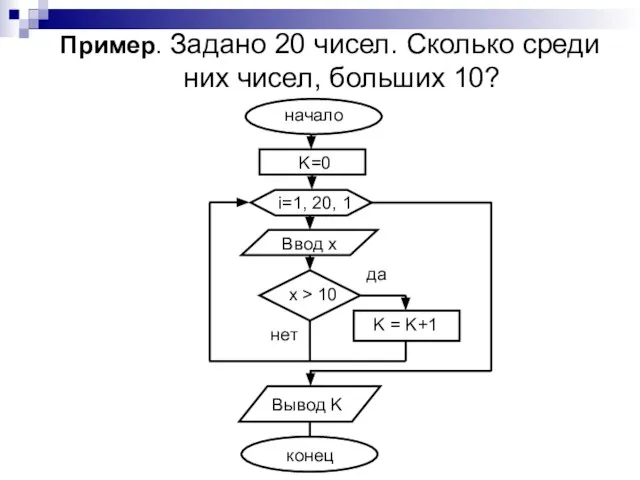
- 26. Пример. Задано 20 чисел. Сколько среди них чисел, больших 10?
- 27. Правило счетчика: начальное значение счетчика K=0; в теле некоторой циклической конструкции выполнить команду: K = K
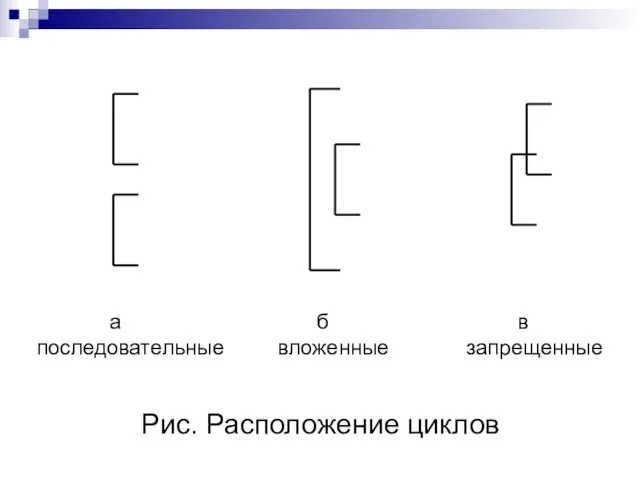
- 28. Рис. Расположение циклов а б в последовательные вложенные запрещенные
- 29. Алгоритм любой задачи может быть представлен как комбинация представленных выше элементарных алгоритмических структур, поэтому данные конструкции:
- 30. Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо
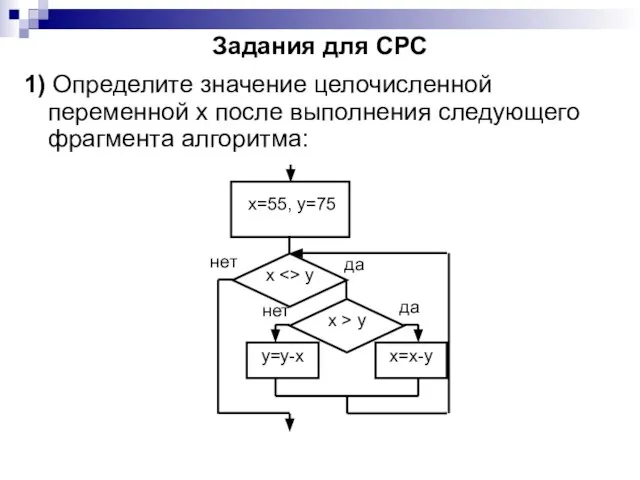
- 31. Задания для СРС 1) Определите значение целочисленной переменной х после выполнения следующего фрагмента алгоритма:
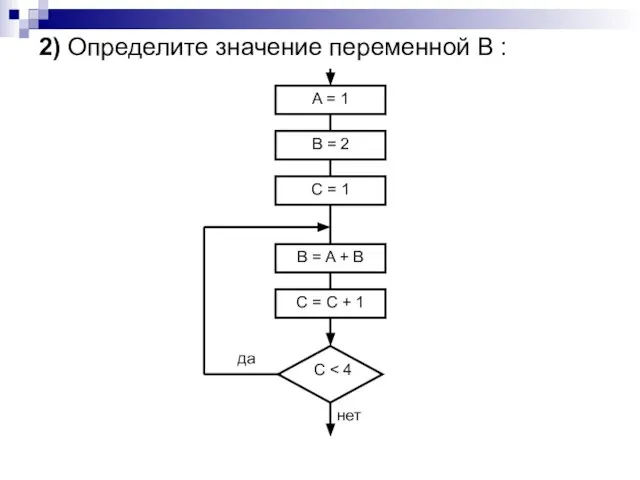
- 32. 2) Определите значение переменной В :
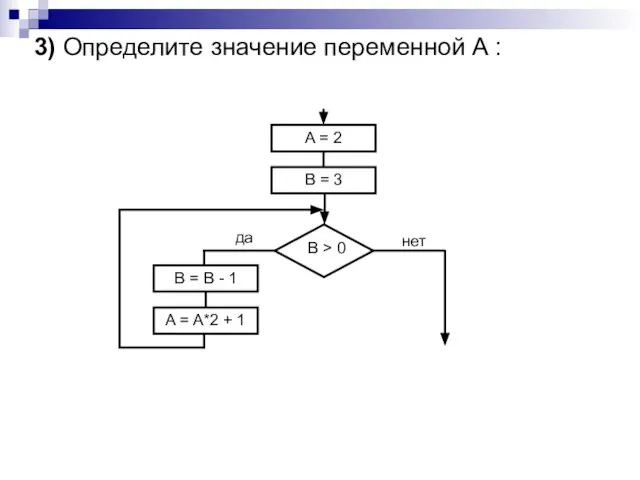
- 33. 3) Определите значение переменной А :
- 34. Контрольные вопросы Дайте определение понятия алгоритма и перечислите его свойства Перечислите способы описания алгоритмов Перечислите основные
- 35. Список рекомендуемых источников 1. Марк Лутц. Программирование на Python. Тома 1 и 2, 4-е издание. –
- 36. Список дополнительных источников www.intuit.ru Язык программирования Python. Саммерфилд М. Программирование на Python 3. Подробное руководство. Пер.
- 38. Скачать презентацию






















 Влияние качества контента на продвижение аккаунта. Компания МЕТЕМ - от проектирования до монтажа
Влияние качества контента на продвижение аккаунта. Компания МЕТЕМ - от проектирования до монтажа Release readiness metrics
Release readiness metrics Baby Blog. ru
Baby Blog. ru Информационная безопасность. Основные понятия
Информационная безопасность. Основные понятия Наследование: class MyClass : Базовый класс, Интерфейс1, Интерфейс2
Наследование: class MyClass : Базовый класс, Интерфейс1, Интерфейс2 Исследователи и ученые России. Книжная выставка
Исследователи и ученые России. Книжная выставка Почта и журналистика
Почта и журналистика Desktop (b) english version
Desktop (b) english version Как турагенту получать 300-500 заявок в месяц на подбор тура и продавать по ним
Как турагенту получать 300-500 заявок в месяц на подбор тура и продавать по ним Linux. Файлы и права доступа в Linux
Linux. Файлы и права доступа в Linux The Greetings Song
The Greetings Song Электронное образование в Республике Татарстан
Электронное образование в Республике Татарстан Python_Циклы
Python_Циклы Кратчайший путь в графе
Кратчайший путь в графе Социальные сети на 01.08.18
Социальные сети на 01.08.18 Моделирование — это метод познания, состоящий в создании и исследовании моделей
Моделирование — это метод познания, состоящий в создании и исследовании моделей Антипаттерны
Антипаттерны Языки программирования
Языки программирования Представление текстовой информации в ПК
Представление текстовой информации в ПК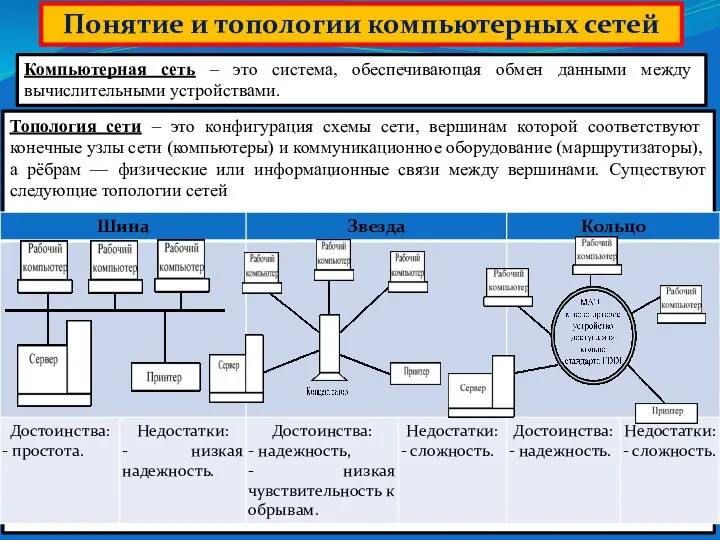 Понятие и топологии компьютерных сетей
Понятие и топологии компьютерных сетей Информация и ее кодирование
Информация и ее кодирование Программное обеспечение ЦСК. Архитектура основных программ
Программное обеспечение ЦСК. Архитектура основных программ Prezentatsia_Microsoft_PowerPoint
Prezentatsia_Microsoft_PowerPoint История слова интернет
История слова интернет Вычисление информационного объема сообщения
Вычисление информационного объема сообщения Компьютерные сети. Тема 4
Компьютерные сети. Тема 4 27 задача ЕГЭ. Информатика
27 задача ЕГЭ. Информатика Логические выражения
Логические выражения