Содержание
- 2. Вариант 1. Перечислить и объяснить суть характеристик случайных событий Летучка Вариант 2. Перечислить и объяснить суть
- 3. Содержание занятия 1. Контроль подготовленности студентов к занятию 2. Решение задач по теме занятия
- 4. Уровни информации Прагматический уровень: I = log2P1 - log2P0 = log2 (P1 / P0) P0 и
- 5. Формула полной вероятности где -Р(В) — вероятность того, что наступило событие В; Р(Аi) — вероятность того,
- 6. Процесс получения информации рассматривается как выбор одного сообщения из конечного наперед заданного множества N равновероятных сообщений,
- 7. Требования к мере количества информации Требования, которым должна удовлетворять мера количества информации, можно сформулировать следующим образом:
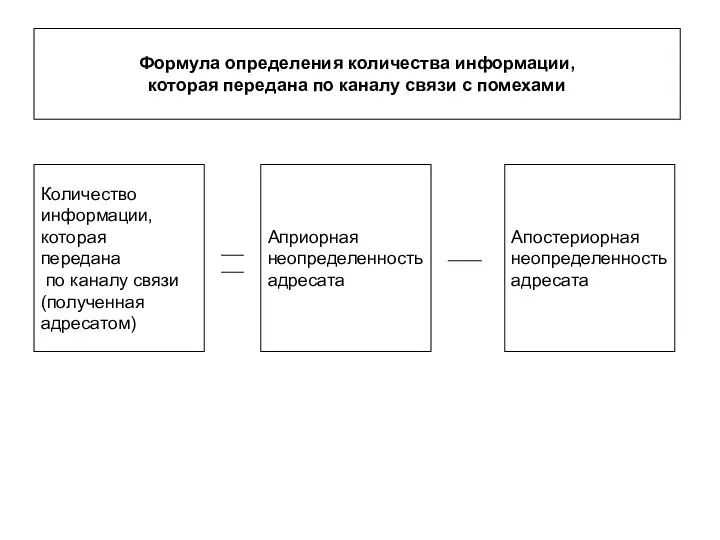
- 8. Априорная неопределенность адресата Апостериорная неопределенность адресата Количество информации, которая передана по каналу связи (полученная адресатом) Формула
- 9. Величина снятой неопределенности должна зависеть от вероятности наступления события (или вероятности принятого сообщения), т.е. чем меньше
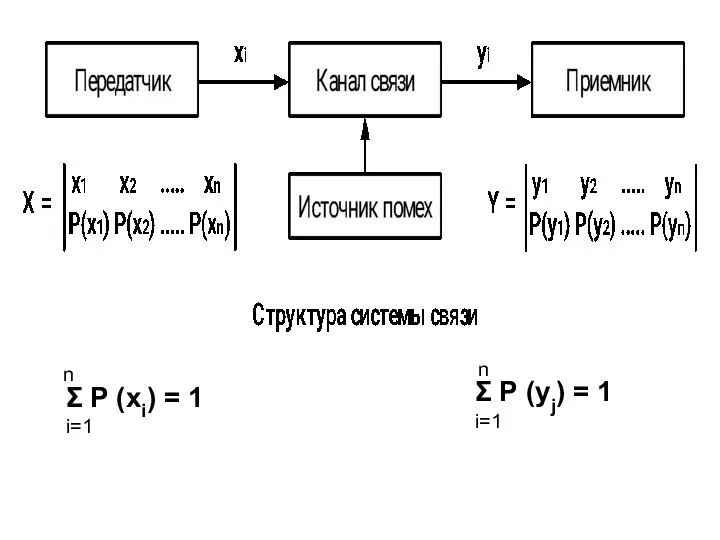
- 10. n Σ Р (хi) = 1 i=1 n Σ Р (уj) = 1 i=1
- 11. Решение задачи № 1 Условие задачи. На узле коммутации пакетов сообщений три маршрутизатора (М1, М2, М3)
- 12. Обсуждение хода решения задачи 1 1) Определение событий, которые возможны в системе? *В чем состоит суть
- 13. 1) Определение сути возможных в системе событий *Суть события А состоит в том, что выбранное из
- 14. 2) Определение полной (безусловной) вероятности наступления события Полная (безусловная) вероятность наступления события А [Р(А) ] –
- 15. Результат решения 2) Р(В1) = 0,25; Р(В2) = 0,35; Р(В3) = 0,4; Р(А/В1) = 0,05; Р(А/В2)
- 16. 3) Определение вероятности того, что выбранное из ЗУ ошибочное сообщение получено маршрутизатором М1, (М2, М3). Определение
- 17. Результат решения 3) Р(В1/А)=[Р(В1)*Р(А/В1)] / Р(А)=(0,25*0,05) / 0,0345 = 0,362; Р(В2/А) = [Р(В2)*Р(А/В2)] / Р(А) =
- 18. Решение задачи № 2 Условие задачи. В производственном цеху трое рабочих разной квалификации изготавливают параллельно одинаковые
- 19. Обсуждение хода решения задачи 2 1) Определение событий, которые возможны в системе? *) cобытие В –
- 20. Результат решения 1) Безусловная вероятность того, что деталь произвел i-й рабочий: Р(А1) = n1 /N =
- 21. Решение задачи № 3 Условие задачи Сообщение, передаваемое со спутника на Землю, на 70% состоит из
- 22. Обсуждение хода решения задачи 1) Определение всех возможных событий при приеме сообщений: *) событие В0 –
- 23. 3) Определение условных вероятностей перечисленных событий *) Р(А0/В0) – условная вероятность того, что принят «0» при
- 24. 3) Определение условных вероятностей перечисленных событий *) Р(А0/В0) – условная вероятность того, что принят «0» при
- 25. 4) Определение вероятности того, что передатчиком передан «0» при условии что получена «1» [Р(В0/А1)] В соответствии
- 26. Задание № 1 По каналу, подверженному воздействию помех, передается одна из двух команд управления в виде
- 27. Задание 2 Принимаются 2 (две) группы сообщений, объединенных по определенным признакам. В одной группе ошибки могут
- 29. Скачать презентацию













![Результат решения 3) Р(В1/А)=[Р(В1)*Р(А/В1)] / Р(А)=(0,25*0,05) / 0,0345 = 0,362; Р(В2/А) =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/933671/slide-16.jpg)










 Web-программирование. Лекция 5. Шаблоны проектирования
Web-программирование. Лекция 5. Шаблоны проектирования Правила работы и безопасного поведения в компьютерном классе
Правила работы и безопасного поведения в компьютерном классе Использование облачных технологий в деятельности педагога
Использование облачных технологий в деятельности педагога Известия VS Медиазона
Известия VS Медиазона Аудит divine-light.ru_версия 21092022
Аудит divine-light.ru_версия 21092022 Основы музейных коммуникаций
Основы музейных коммуникаций Internet Protocol (IP)
Internet Protocol (IP) ВКонтакте - российская социальная сеть
ВКонтакте - российская социальная сеть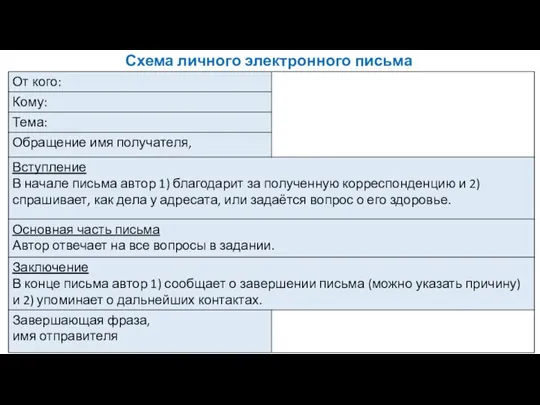 Схема личного электронного письма
Схема личного электронного письма Мобильное электронное образование в детских садах и дома
Мобильное электронное образование в детских садах и дома Базовые показатели эффективности (БПЭ)
Базовые показатели эффективности (БПЭ) Представление звуковой информации
Представление звуковой информации Технология промышленного производства
Технология промышленного производства Сеть для организаций. Отчет о проектной работе
Сеть для организаций. Отчет о проектной работе Умные таблицы Excel 2007-2013
Умные таблицы Excel 2007-2013 Строки как одномерные массивы данных типа char (терминальные строки)
Строки как одномерные массивы данных типа char (терминальные строки) Азбука журналистики
Азбука журналистики Краудсорсинг в ИТ рекрутменте
Краудсорсинг в ИТ рекрутменте Метрология и теория измерений
Метрология и теория измерений одирование тестовой, графической и звуковой информации
одирование тестовой, графической и звуковой информации Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3)
Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3)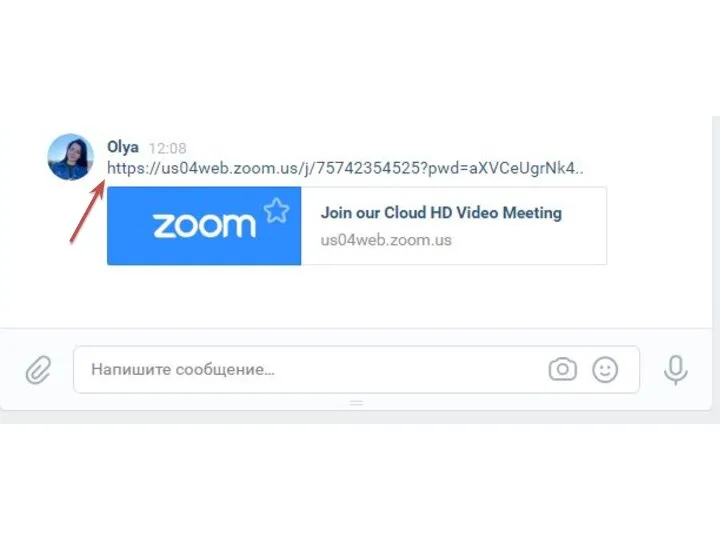 Инструкция по входу в ZOOM
Инструкция по входу в ZOOM Das At-Zeichen
Das At-Zeichen Презентация на тему Поколение ЭВМ
Презентация на тему Поколение ЭВМ  Понятие информация
Понятие информация Web - страницы. Язык HTML
Web - страницы. Язык HTML Ресурсы для защиты информации в веке IT технологий
Ресурсы для защиты информации в веке IT технологий Одномерные массивы целых чисел. Описание, заполнение, вывод массива
Одномерные массивы целых чисел. Описание, заполнение, вывод массива