Содержание
- 2. Словарные операции поиск элемента с заданным ключом х добавление нового элемента с заданным ключом х удаление
- 3. поиск элемента с заданным ключом х произвольный массив O(n) ФПМИ БГУ упорядоченный массив O(log n) поисковое
- 4. добавление элемента с заданным ключом х ФПМИ БГУ произвольный массив O(1) упорядоченный массив O(n) поисковое дерево
- 5. удаление элемента с заданным ключом х ФПМИ БГУ произвольный массив O(n) упорядоченный массив O(n) поисковое дерево
- 6. Сбалансированные деревья
- 7. v w z u x hu hw ФПМИ БГУ
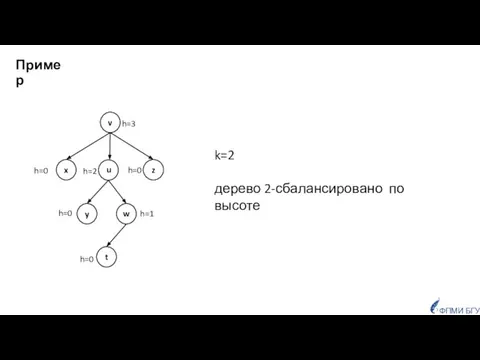
- 8. Пример h=3 h=0 h=0 h=0 h=1 h=2 h=0 k=2 дерево 2-сбалансировано по высоте ФПМИ БГУ v
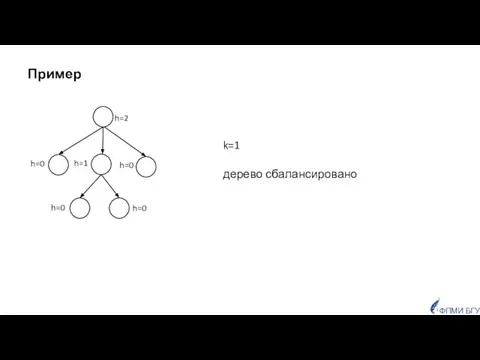
- 9. h=0 k=1 дерево сбалансировано ФПМИ БГУ h=2 h=0 h=0 h=1 h=0 Пример
- 10. Высота полного бинарного дерева h=O(log n), где n – количество вершин. ФПМИ БГУ Полное бинарное дерево
- 11. Идеально сбалансированные деревья ФПМИ БГУ
- 12. v w z u w cu cw ФПМИ БГУ
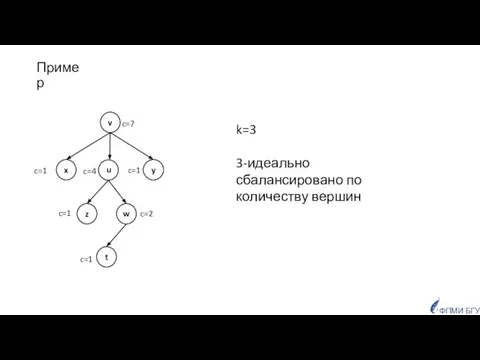
- 13. Пример k=3 3-идеально сбалансировано по количеству вершин ФПМИ БГУ c=7 c=1 c=1 c=1 c=2 c=4 c=1
- 14. ФПМИ БГУ Каждое идеально-сбалансированное дерево является сбалансированным. Обратное верно не всегда. Дерево –сбалансировано, но не является
- 15. Оценки для бинарных поисковых деревьев 10 18 19 6 2 построение дерева для последовательности из n
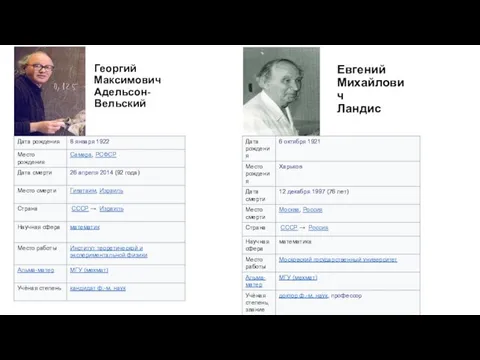
- 16. ФПМИ БГУ В 1962 году советские учёные Г.М.Адельсон-Вельский и Е.М.Ландис предложили структуру данных сбалансированного поискового дерева.
- 17. Георгий Максимович Адельсон-Вельский Евгений Михайлович Ландис
- 18. АВЛ-дерево – это бинарное поисковое дерево, которое является сблансированным по высоте. 2 4 1 3 5
- 19. АВЛ-дерево ? Нет, так как оно не поисковое. 8 4 1 3 5 ФПМИ БГУ НЕТ
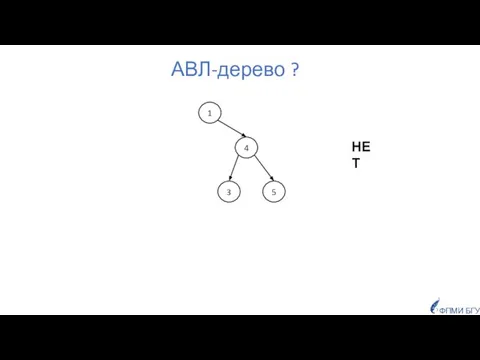
- 20. АВЛ-дерево ? 1 4 3 5 ФПМИ БГУ НЕТ
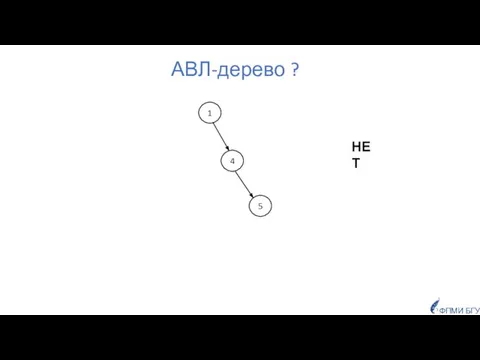
- 21. АВЛ-дерево ? 1 4 5 ФПМИ БГУ НЕТ
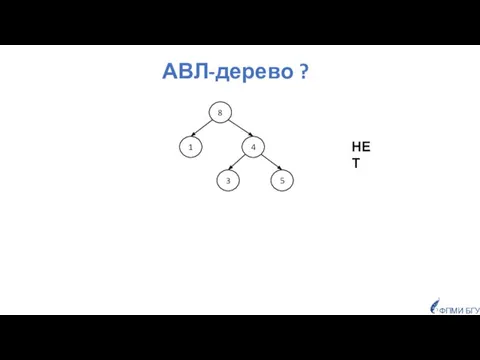
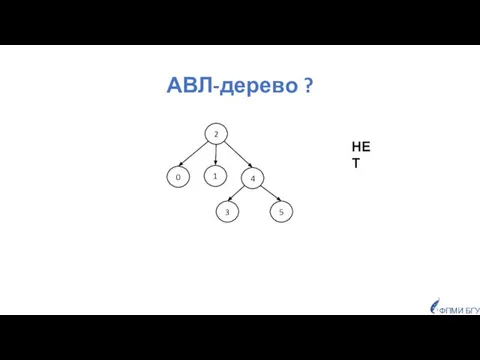
- 22. АВЛ-дерево ? 2 4 3 5 0 1 ФПМИ БГУ НЕТ
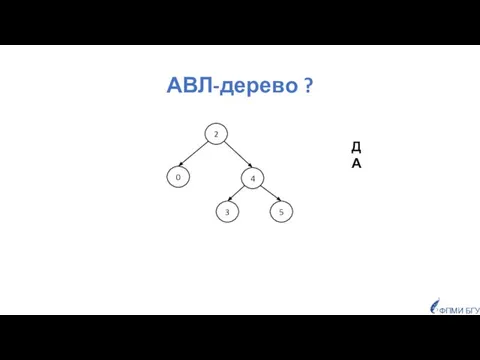
- 23. АВЛ-дерево ? 2 4 3 5 0 ФПМИ БГУ ДА
- 24. ТЕОРЕМА Пусть n – число внутренних вершин АВЛ-дерева, h – его высота. Тогда справедливы следующие неравенства:
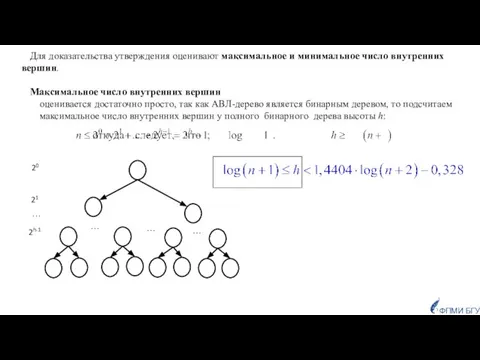
- 25. Для доказательства утверждения оценивают максимальное и минимальное число внутренних вершин. Максимальное число внутренних вершин оценивается достаточно
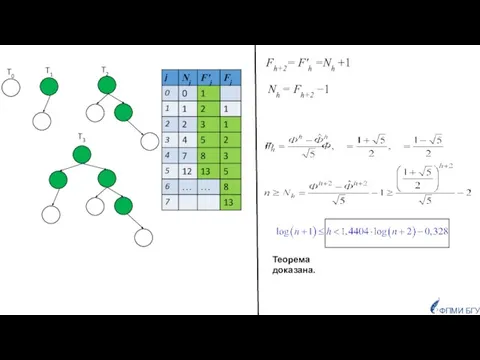
- 26. Для оценки минимального числа внутренних вершин используются свойства чисел Фибоначчи. Пусть Nh − число внутренних вершин
- 27. ФПМИ БГУ T0 T1 T2 T3 Fh+2= F'h =Nh +1 Теорема доказана. Nh = Fh+2 −1
- 28. ФПМИ БГУ Операции поиска, добавления и удаления элементов для АВЛ-деревьев осуществляются точно также, как и для
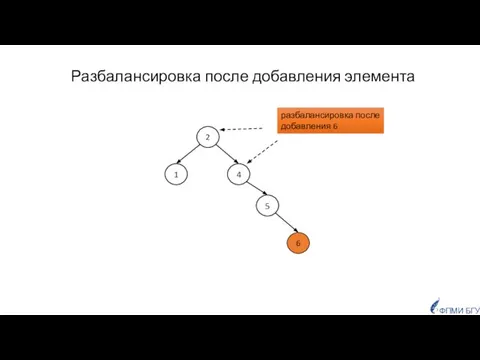
- 29. Разбалансировка после добавления элемента 2 4 1 5 6 разбалансировка после добавления 6 ФПМИ БГУ
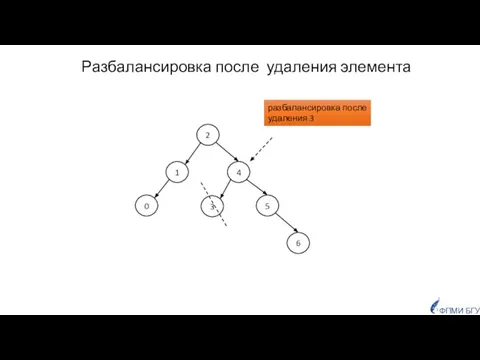
- 30. Разбалансировка после удаления элемента 2 4 1 5 6 разбалансировка после удаления 3 3 0 ФПМИ
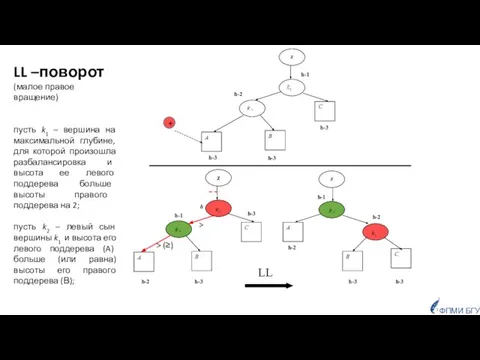
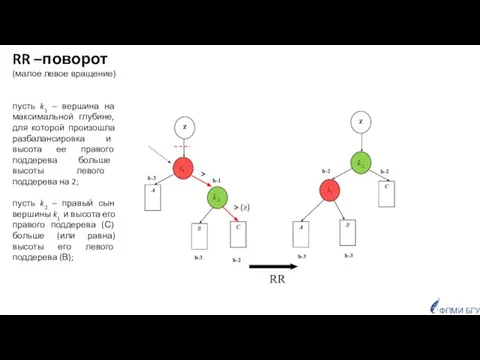
- 31. Балансировки LL поворот (малое правое вращение, одинарный правый поворот) RR поворот (малое левое вращение, одинарный левый
- 32. h-1 h-3 h-1 h z C A B z B A C h-2 h-3 h-3 h-3
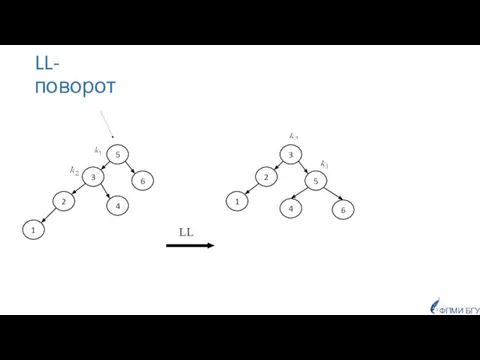
- 33. LL-поворот 5 3 6 2 4 3 2 5 1 4 6 ФПМИ БГУ 1 LL
- 34. RR h-3 h-1 h-2 h-2 z C A B z B A C h-3 h-3 h-2
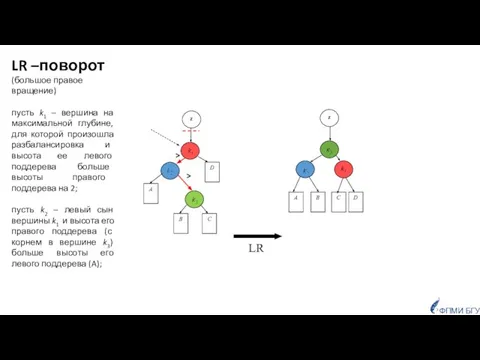
- 35. z C A B z B A D C D h-2 h-3 h-4 h-3 h-1 h-3
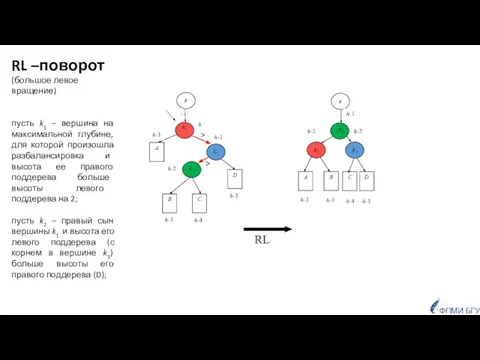
- 36. z C A B z B D A D C > > ФПМИ БГУ LR –поворот
- 37. ОЦЕНКИ Каждый из поворотов (LL, RR, LR, RL) выполняется за O(1), если известна ссылка на разбалансированную
- 38. ФПМИ БГУ После выполнения операции добавления элемента разбалансировка может произойти сразу у нескольких вершин (эти вершины
- 39. ФПМИ БГУ Процедура добавления элемента: поиск отца для вершины x ; добавление вершины x; поиск разбалансированнной
- 40. При удалении элемента x разбалансировка может произойти только у одной вершины: найдём разбалансированную вершину и выполним
- 41. ПРИМЕР
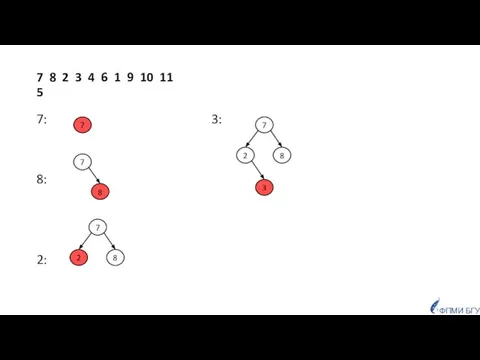
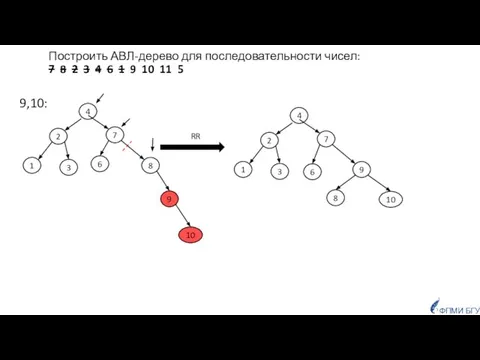
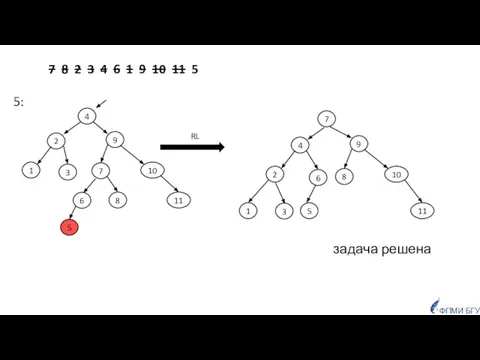
- 42. Построить АВЛ-дерево для последовательности чисел: 7, 8, 2, 3, 4, 6, 1, 9, 10, 11, 5
- 43. 7 8 2 3 4 6 1 9 10 11 5 7: 3: 8: 2: 7
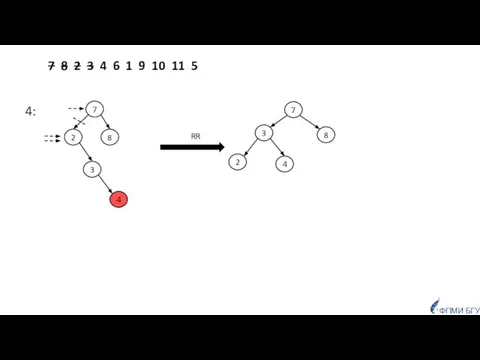
- 44. 7 8 2 3 4 6 1 9 10 11 5 4: 7 8 2 3
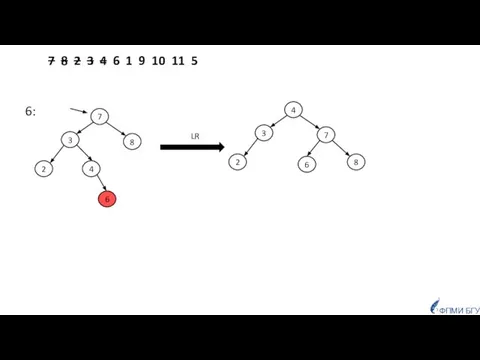
- 45. 7 8 2 3 4 6 1 9 10 11 5 6: LR 7 3 8
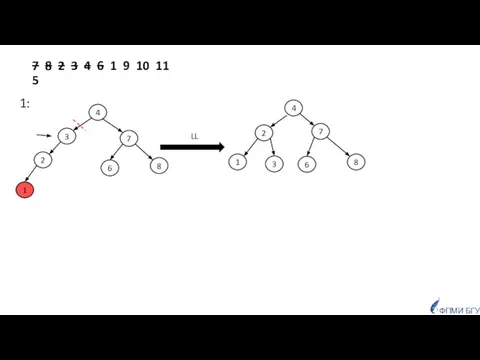
- 46. 7 8 2 3 4 6 1 9 10 11 5 1: LL 2 7 1
- 47. Построить АВЛ-дерево для последовательности чисел: 7 8 2 3 4 6 1 9 10 11 5
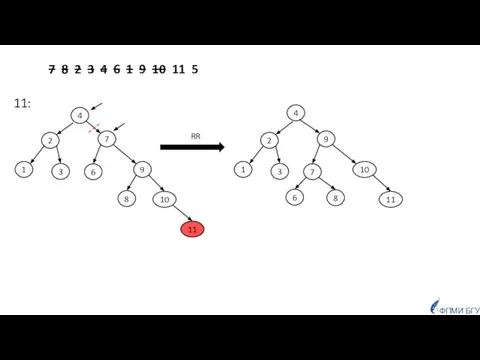
- 48. 7 8 2 3 4 6 1 9 10 11 5 11: RR 2 9 1
- 49. 7 8 2 3 4 6 1 9 10 11 5 5: задача решена RL 2
- 50. 7, 8, 2, 3, 4, 6, 1, 9, 10, 11, 5 4 9 2 8 10
- 51. Сортировка деревом Предположим, что на вход поступаю числа, среди которых нет повторяющихся. 1. По последовательности чисел
- 52. Абстрактный тип данных: множество (set) Множество (англ. set) —хранит набор попарно различных объектов без определённого порядка.
- 53. Абстрактный тип данных ассоциативный массив (map) Ассоциативный массив (англ. associative array), или отображение (англ. map), или
- 55. Скачать презентацию



























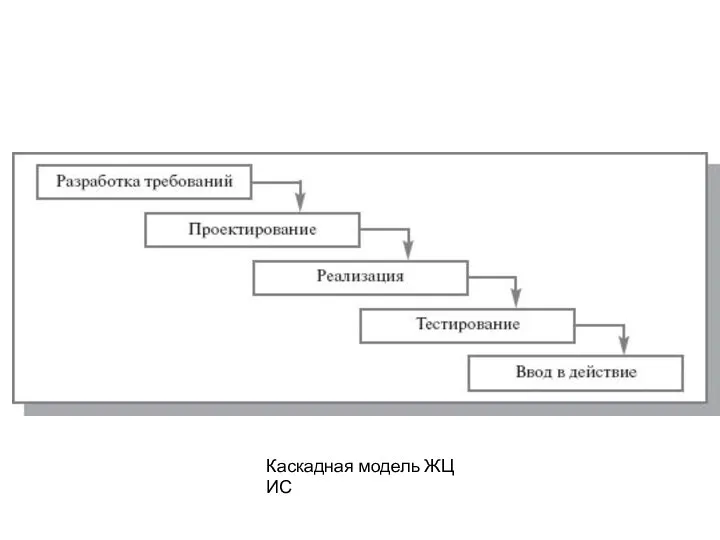 Каскадная модель ЖЦ ИС
Каскадная модель ЖЦ ИС Связи объектов Access
Связи объектов Access Трассировка пиксельных изображений
Трассировка пиксельных изображений Создание и разработка гексакоптера
Создание и разработка гексакоптера Кодирование информации
Кодирование информации Тест для выпускников 2021. Фотография
Тест для выпускников 2021. Фотография Методика SMART
Методика SMART Поиск и работа с почтой
Поиск и работа с почтой Cp2000 series training notes
Cp2000 series training notes На каких трех китах держится информатика? Логика, алгоритмы и программа
На каких трех китах держится информатика? Логика, алгоритмы и программа Проектирование базы данных. Определение предметной области. Уровни представления данных
Проектирование базы данных. Определение предметной области. Уровни представления данных Организация циклов. Оператор цикла
Организация циклов. Оператор цикла ليلى عثمان باحلى الموضاعت التعليمية
ليلى عثمان باحلى الموضاعت التعليمية Платформа .Net
Платформа .Net Презентация на тему История создания сети Интернет
Презентация на тему История создания сети Интернет  Создание интенет-магазинов
Создание интенет-магазинов Программно-аппаратные методы защиты информации. Цифровые водяные знаки
Программно-аппаратные методы защиты информации. Цифровые водяные знаки Информационные системы
Информационные системы Фотообои. Правки сайта
Фотообои. Правки сайта Основные примитивы AutoCad при создании графических объектов
Основные примитивы AutoCad при создании графических объектов Профессия - экокомпьютерщик
Профессия - экокомпьютерщик Программное обеспечение. Автоматизированная система Smart Banking Solutions (АС SBS)
Программное обеспечение. Автоматизированная система Smart Banking Solutions (АС SBS) Актуальные data-опции для корпоративных клиентов
Актуальные data-опции для корпоративных клиентов Миллион новостей - одно SOZVEZDIE
Миллион новостей - одно SOZVEZDIE Errori sito Factory Tour
Errori sito Factory Tour Инструктаж по готовому примеру LineCross
Инструктаж по готовому примеру LineCross Выпускная квалификационная работа: применение XML технологий на MS SQL для сопровождения корпоративных приложений
Выпускная квалификационная работа: применение XML технологий на MS SQL для сопровождения корпоративных приложений Что такое моделирование?
Что такое моделирование?