Математика в музыке

Пифагор
Пифагор (570 – 490 года до н.э.)– древнегреческий математик, философ. Родился Пифагор в Сидоне Финикийском.

Звучание струны
Скрипичная струна звучит потому, что смычок заставляет колебаться струны. Струны, в свою очередь, заставляют колебаться воздух и образуют волны. А те уже попадают к нам в уши, заставляя вибрировать барабанные перепонки. И тогда мы слышим прекрасную музыку.

Современному композитору трудно представить сочинение вокальной и инструментальной музыки в отсутствие таких понятий, как интервал, гамма, музыкальный строй. Естественно, что на протяжении многих веков люди не знали этих слов. В таком случае возникает вопрос: кто же стоял у истоков построения мажора и минора, аккордов и интервалов? А у истоков стоял не кто иной, как великий математик Пифагор. Его открытие в области теории музыки послужило базой для развития математических пропорций в музыке.
Звуковые соотношения

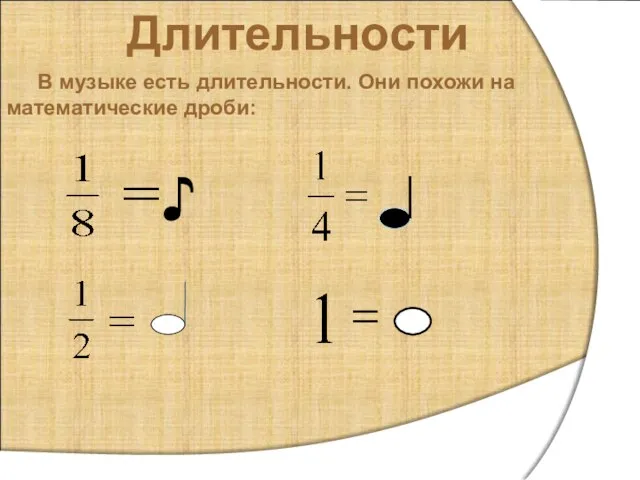
Длительности
В музыке есть длительности. Они похожи на математические дроби:

Произведение
1) Музыкальное произведение можно представить в виде математического примера. Возьмем детское произведение из сборника педагогического репертуара для фортепиано 1 класса. Оно называется «Белочка»:
Это произведение можно разложить так:
Это только 1-ый такт. В нём 4 дроби , потому-что размер произведения четыре четверти. Также раскладываются и остальные такты.

-второй такт
-первый такт
-третий такт
2) Рассмотрим следующее, более сложное произведение из того же сборника. Оно называется: « Со вьюном хожу»:
Размер произведения четыре четверти. Возьмём первые три такта.

3)Пойдём дальше и рассмотрим произведение с более сложным размером. Отрывок из произведения для 6 класса «Цветы Амстердама»:
Размер произведения три восьмых. Так как произведение начинается из-за такта (первый такт неполный) начнём с второго такта.
- это второй такт

4) Произведение, как и предыдущее 6 класса. Оно называется «Рондо»:
Размер этого произведения шесть восьмых. Так же как и предыдущее произведения, оно начинается из-за такта, поэтому мы рассмотрим 2 такт.
или можно так

Заключение
В своей работе я установила связь между математическими и музыкальными дробями и выяснила, кто стоял у истоков теории музыки.