Содержание
- 2. Лекция 8. Криптографическая система RSA План лекции: 2. Алгоритм шифрования RSA 1. Введение 3. Расшифрование RSA
- 3. Лекция 8. Криптографическая система RSA 1. Введение RSA – криптографическая система открытого ключа, обеспечивающая такие механизмы
- 4. Лекция 8. Криптографическая система RSA Его криптостойкость основывается на сложности разложения на множители больших чисел, а
- 5. Лекция 8. Криптографическая система RSA 2. Алгоритм шифрования RSA Сгенерировать открытый и секретные ключи: Возьмем два
- 6. Лекция 8. Криптографическая система RSA Определим такое число е (1 (e*d) mod ((p-1)*(q-1))=1. Назовем открытым ключом
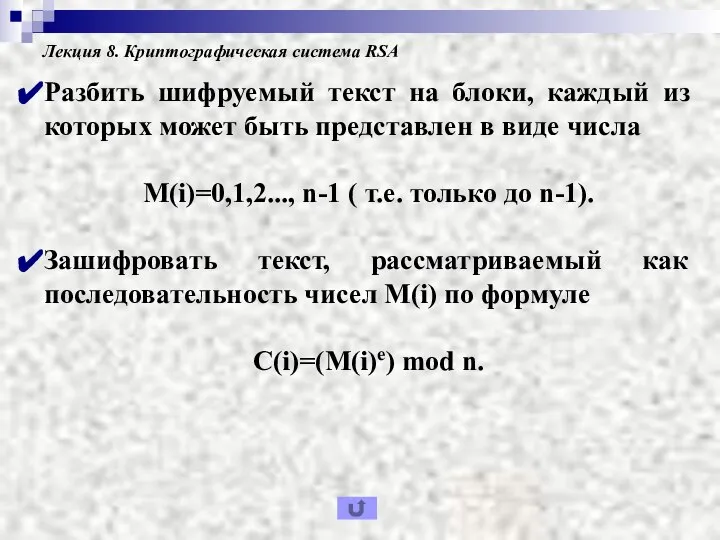
- 7. Лекция 8. Криптографическая система RSA Разбить шифруемый текст на блоки, каждый из которых может быть представлен
- 8. Лекция 8. Криптографическая система RSA 3. Расшифрование RSA Чтобы расшифровать данные, используя секретный ключ {d, n},
- 9. Лекция 8. Криптографическая система RSA Пример. Рассмотрим небольшой пример, иллюстрирующий применение алгоритма RSA. Пусть требуется зашифровать
- 10. Лекция 8. Криптографическая система RSA 1 шаг. Выберем p = 3 и q = 11. 2
- 11. Лекция 8. Криптографическая система RSA 5 шаг. Представим шифруемое сообщение как последовательность целых чисел в диапазоне
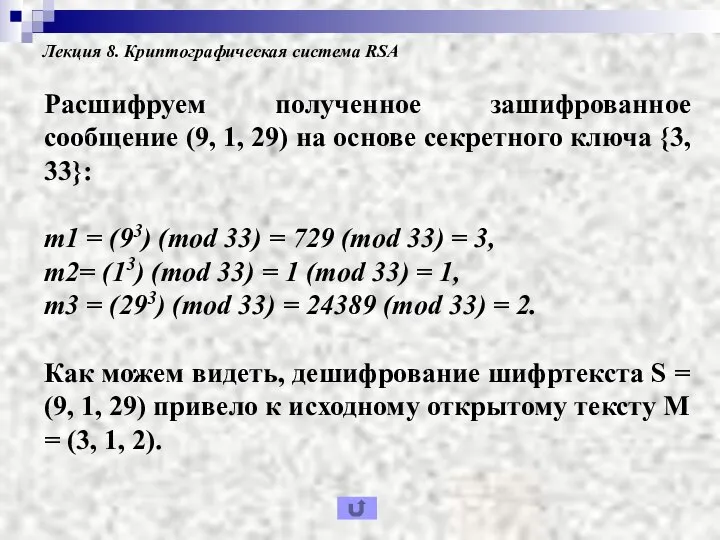
- 12. Лекция 8. Криптографическая система RSA Расшифруем полученное зашифрованное сообщение (9, 1, 29) на основе секретного ключа
- 13. Лекция 8. Криптографическая система RSA Замечание. Делители p и q можно уничтожить или сохранить вместе с
- 14. Лекция 8. Криптографическая система RSA 4. Особенности применения криптографической системы RSA Криптосистема RSA может использоваться для
- 15. Лекция 8. Криптографическая система RSA Скорость работы алгоритма RSA. Как при шифровании и расшифровке, так и
- 16. Лекция 8. Криптографическая система RSA При этом шифрование данных идет быстрее чем расшифровка, а проверка подписи
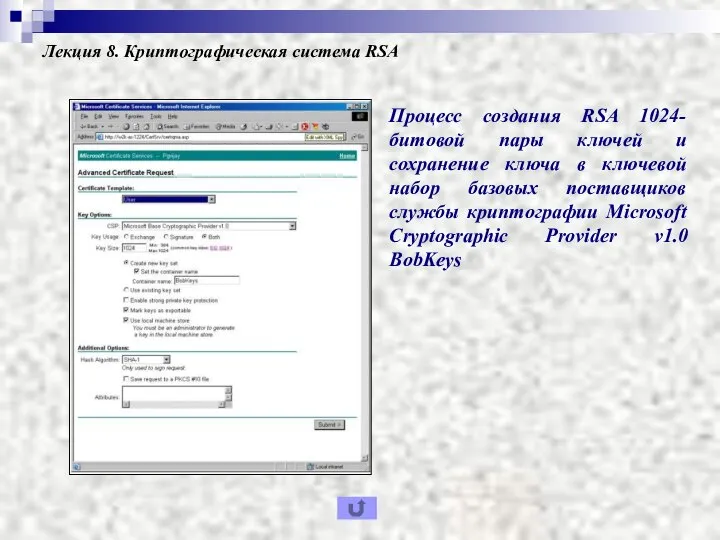
- 17. Лекция 8. Криптографическая система RSA Процесс создания RSA 1024-битовой пары ключей и сохранение ключа в ключевой
- 18. Лекция 8. Криптографическая система RSA Способы взлома криптосистемы RSA. Существует несколько способов взлома RSA. Наиболее эффективная
- 19. Лекция 8. Криптографическая система RSA Такую атаку можно провести, найдя главные сомножители общего модуля n –
- 20. Лекция 8. Криптографическая система RSA Усовершенствование вычислительного оборудования само по себе не уменьшит стойкость криптосистемы RSA,
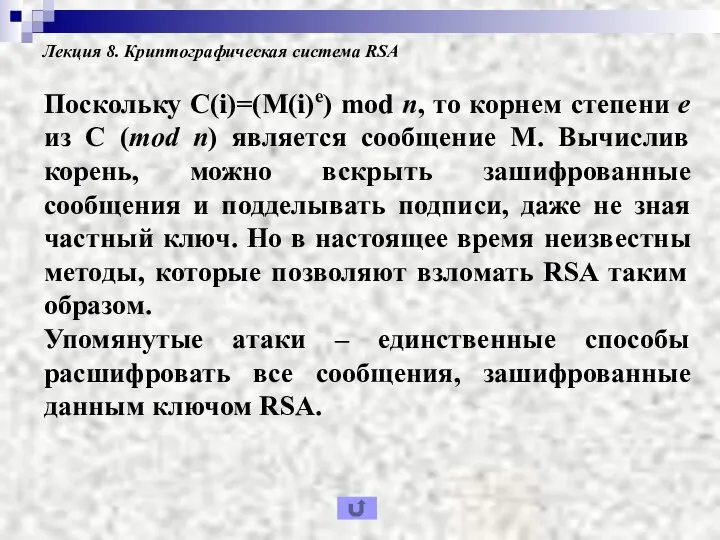
- 21. Лекция 8. Криптографическая система RSA Поскольку C(i)=(M(i)e) mod n, то корнем степени e из С (mod
- 22. Лекция 8. Криптографическая система RSA Рекомендуемая длина ключа. Размер ключа в алгоритме RSA связан с размером
- 23. Лекция 8. Криптографическая система RSA Если два числа чрезвычайно близки друг к другу или их разность
- 24. Лекция 8. Криптографическая система RSA По теореме о Простых Числах количество простых чисел, меньших некоторого n
- 25. Лекция 8. Криптографическая система RSA Контрольные вопросы: 1. На чем основывается криптостойкость RSA? 2. Сформулировать алгоритм
- 26. Список используемых источников: Бубнов А.А. Основы информационной безопасности. – М.: Академия, 2017. - 256 с. Ерохин
- 28. Скачать презентацию



















 Здоровье ребенка в наших руках
Здоровье ребенка в наших руках Тема 2.2. ПОО СПб Ник. - 21
Тема 2.2. ПОО СПб Ник. - 21 Телевидение - друг или враг
Телевидение - друг или враг Наркомания, курение, алкоголизм
Наркомания, курение, алкоголизм Медицинская помощь на судне
Медицинская помощь на судне Время разложения различного бытового мусора
Время разложения различного бытового мусора Согревание в лесу. Как не замерзнуть в природных условиях
Согревание в лесу. Как не замерзнуть в природных условиях Мы – за мир, без терроризма
Мы – за мир, без терроризма Возникновение пожаров с участием детей
Возникновение пожаров с участием детей Мир без наркотиков
Мир без наркотиков Мобильное приложение Безопасная железная дорога
Мобильное приложение Безопасная железная дорога Чрезвычайные ситуации гидрологического характера
Чрезвычайные ситуации гидрологического характера Доклад начальника отдела оперативно-аналитического ЦУКС
Доклад начальника отдела оперативно-аналитического ЦУКС ЧС техногенного характера полная версия (1)
ЧС техногенного характера полная версия (1) Правила поведения зимой
Правила поведения зимой Техника безопасности на уроках музыки
Техника безопасности на уроках музыки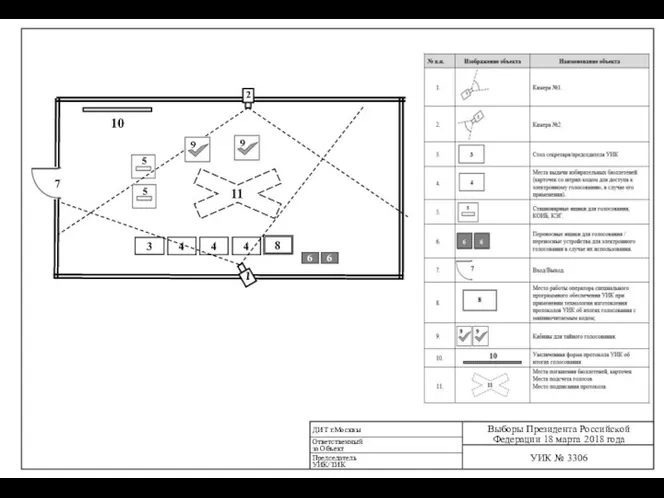 Система видеонаблюдения на избирательном участке
Система видеонаблюдения на избирательном участке Интерактивная игра для детей 5-7 лет Незнайка в большом городе
Интерактивная игра для детей 5-7 лет Незнайка в большом городе Годовщина Чернобыльской трагедии
Годовщина Чернобыльской трагедии Трезвость - норма жизни
Трезвость - норма жизни Перечень противопожарных мероприятий, выполняемых лесопользователями
Перечень противопожарных мероприятий, выполняемых лесопользователями Презентация на тему Паспорт безопасности
Презентация на тему Паспорт безопасности  Безопасное путешествие
Безопасное путешествие ЧС природного характера
ЧС природного характера Пожарная тревога. Игра
Пожарная тревога. Игра Роль игры в организации кружковой внеаудиторной работы по охране труда и безопасности жизнедеятельности в ГПОУ
Роль игры в организации кружковой внеаудиторной работы по охране труда и безопасности жизнедеятельности в ГПОУ Здоровый образ жизни
Здоровый образ жизни История Правил дорожного движения с 2100 по 2200 годы. Команда Поворот не туда
История Правил дорожного движения с 2100 по 2200 годы. Команда Поворот не туда