Содержание
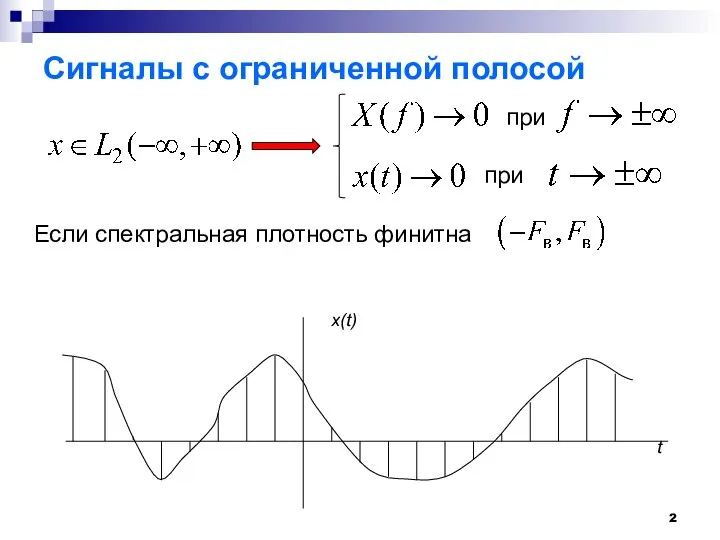
- 2. Сигналы с ограниченной полосой Если спектральная плотность финитна t x(t) при при
- 3. Теорема отсчётов Э. Уиттекер - 1915 Х. Найквист - 1928 В.А. Котельников - 1933 К. Шеннон
- 4. Котельников В.А. ”О пропускной способности «эфира» и проволоки в электросвязи”. В сб. Всесоюзный энергетический комитет. Материалы
- 5. Теорема отсчётов Представим комплексным рядом Фурье Э. Уиттекер - 1915 Х. Найквист - 1928 В.А. Котельников
- 6. Теорема отсчетов Котельникова Выразим сигнал
- 7. Коэффициенты ряда Фурье
- 8. Обозначим
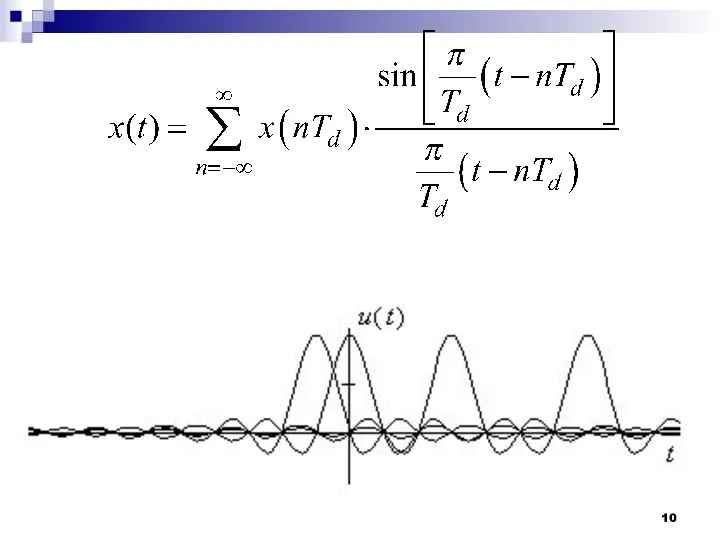
- 9. Теорема отсчётов Котельникова Итак базисные функции
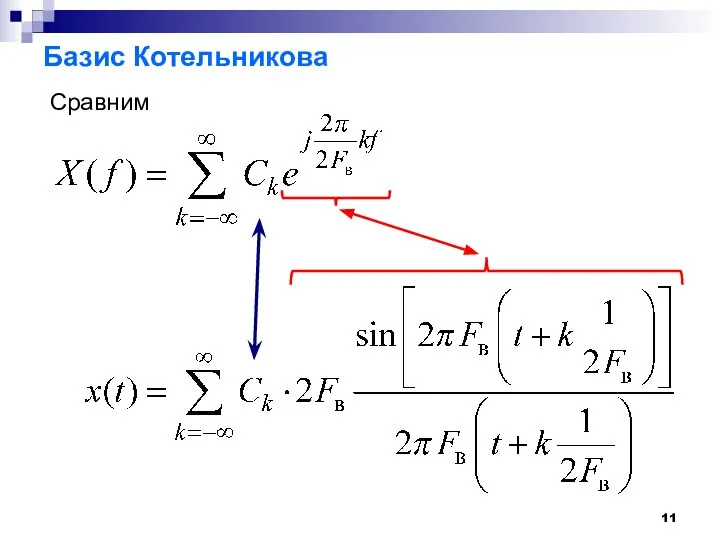
- 11. Базис Котельникова Сравним
- 12. согласно обобщённой формуле Рэлея
- 13. Базис ортогональный ненормированный
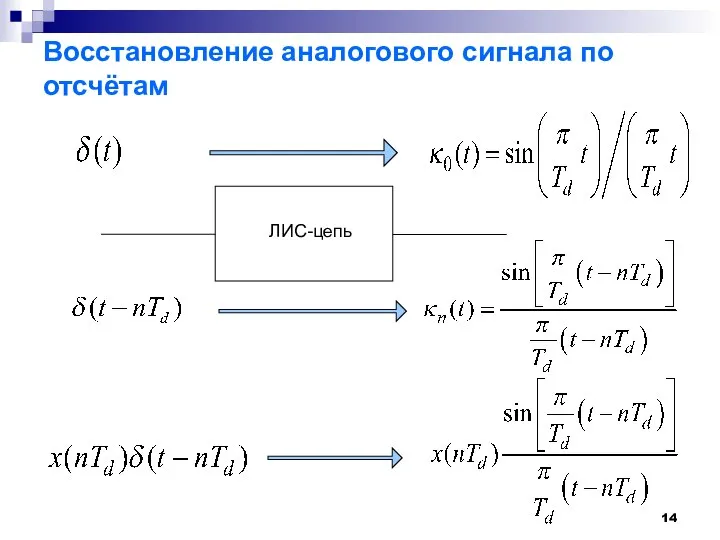
- 14. Восстановление аналогового сигнала по отсчётам ЛИС-цепь
- 15. Осталось просуммировать по n ЛИС-цепь
- 16. Спектральная трактовка ЛИС-цепь Воздействие (иАИМ-сигнал) где 0
- 17. Согласно теореме умножения ряд Фурье с коэффициентами Поэтому спектральная плотность
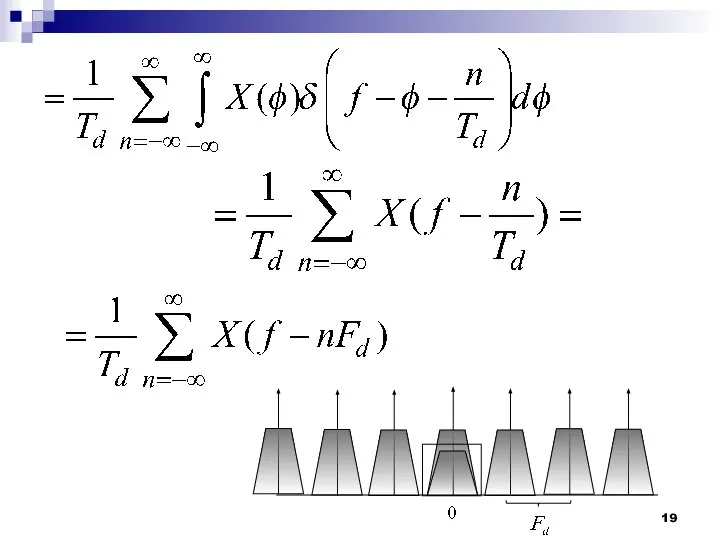
- 18. Спектральная плотность
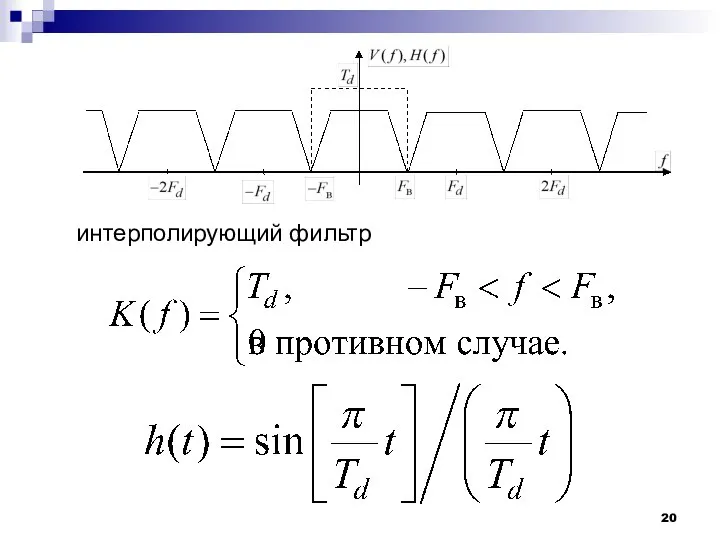
- 20. интерполирующий фильтр
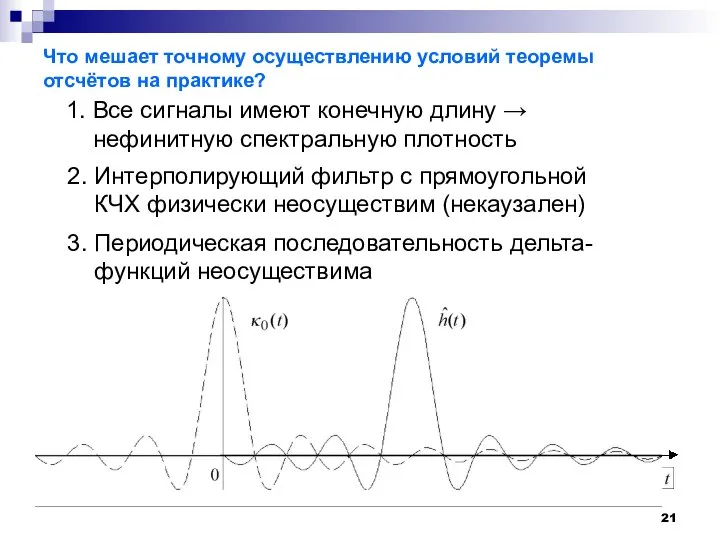
- 21. Что мешает точному осуществлению условий теоремы отсчётов на практике? 1. Все сигналы имеют конечную длину →
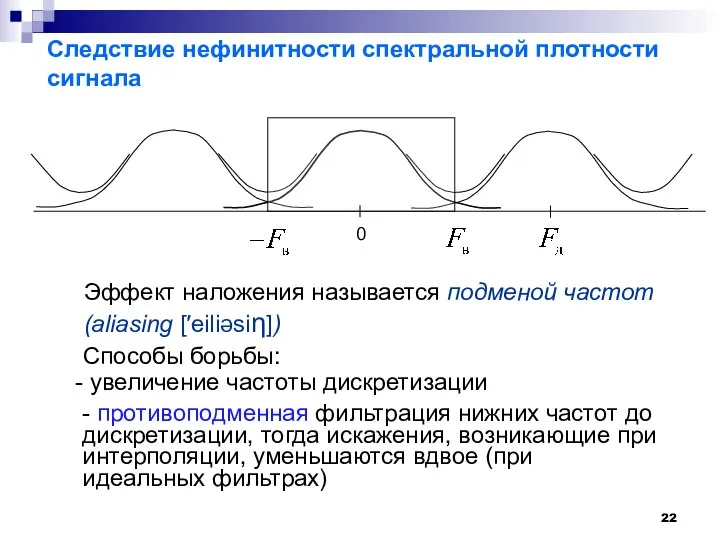
- 22. Следствие нефинитности спектральной плотности сигнала 0 Эффект наложения называется подменой частот (aliasing [′eiliəsiη]) Способы борьбы: увеличение
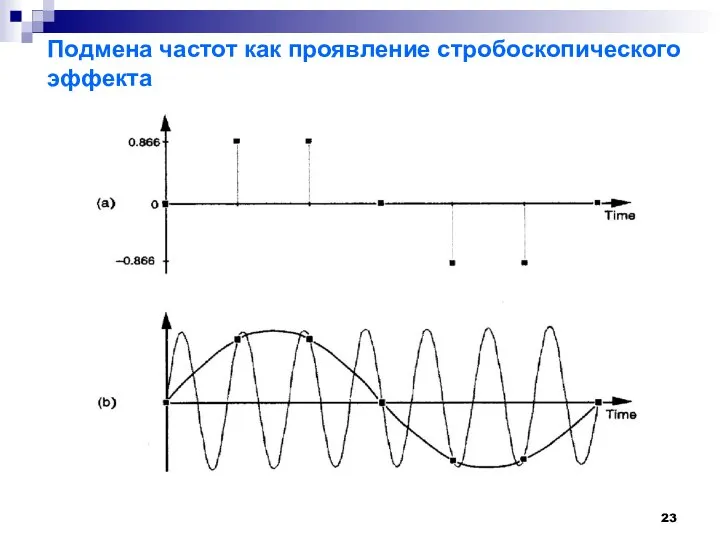
- 23. Подмена частот как проявление стробоскопического эффекта
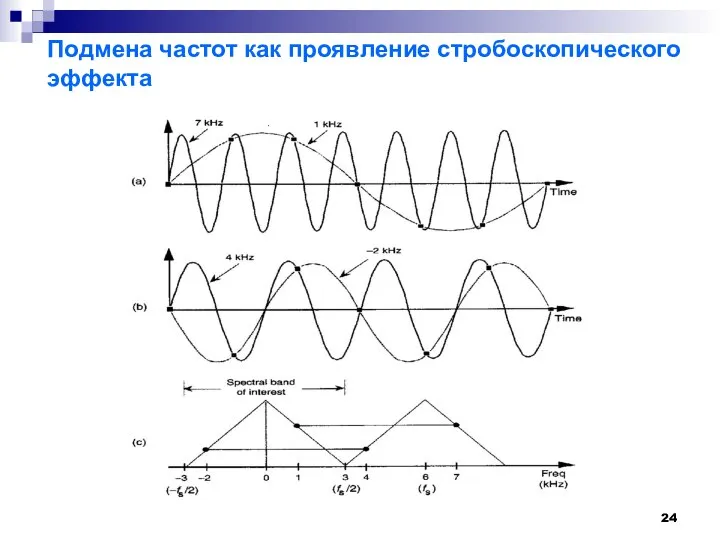
- 24. Подмена частот как проявление стробоскопического эффекта
- 26. Скачать презентацию













 Фесиваль-конкурс Вкус и польза постных блюд
Фесиваль-конкурс Вкус и польза постных блюд Город Тула
Город Тула Психологические последствия массовых коммуникаций
Психологические последствия массовых коммуникаций Час истории
Час истории Презентация на тему Сочинение описание животного (5 класс)
Презентация на тему Сочинение описание животного (5 класс) Битва за Москву
Битва за Москву Digital BTL: эффективность интерактивных каналов в BTL-акциях. - презентация
Digital BTL: эффективность интерактивных каналов в BTL-акциях. - презентация Сенсорная интеграция
Сенсорная интеграция Динамическая геометрия, Тихомирова С.В
Динамическая геометрия, Тихомирова С.В События, о которых помнит город и страна
События, о которых помнит город и страна Удивительный мир музыкальных образов
Удивительный мир музыкальных образов Субтропическая зона
Субтропическая зона Управление непрофильными активами
Управление непрофильными активами Практические аспекты обеспечения безопасности облачных вычислений
Практические аспекты обеспечения безопасности облачных вычислений Природоохранное законодательство штата Аляска:Требования для предприятий отрасли по разливам
Природоохранное законодательство штата Аляска:Требования для предприятий отрасли по разливам Цепи PEWAG для лесной техники Economy Plus Helt Perfekt STN Helt Perfekt Soft.
Цепи PEWAG для лесной техники Economy Plus Helt Perfekt STN Helt Perfekt Soft. Игра в имена
Игра в имена Презентация на тему История часов
Презентация на тему История часов Практика
Практика Ваши права и права других людей
Ваши права и права других людей ООО Центр развития ребенка Спектр. Подбор персонала
ООО Центр развития ребенка Спектр. Подбор персонала Социолингвистические особенности английского языка в арабских странах
Социолингвистические особенности английского языка в арабских странах ЭДЕКТРОДУГОВОЙ НАГРЕВ
ЭДЕКТРОДУГОВОЙ НАГРЕВ Моделирование влияния либерализации внешней торговли на благосостояние страны
Моделирование влияния либерализации внешней торговли на благосостояние страны Внутренние причины наиболее стойких мотиваций поведения
Внутренние причины наиболее стойких мотиваций поведения Иркутский государственный университет. Кафедра романо-германской филологии
Иркутский государственный университет. Кафедра романо-германской филологии Тема: Таблица единиц времени.
Тема: Таблица единиц времени. Информация о приеме в Вятский государственный университет в 2021 г
Информация о приеме в Вятский государственный университет в 2021 г