Слайд 2Основная часть
Зачем нужны движения в ходе решения мыслительной задачи?
Или грустная история о

репликации с продолжением
Слайд 3НЕМНОГО ОБ EMBODIED COGNITION
Ф. Варела, Э. Томпсон и Э. Рош «Воплощенный разум:

когнитивная наука и человеческий опыт» (F.J. Varela, E. Thompson, E. Rosch, 1991):
Опора человеческого познания на телесную активность и проявления, а также на взаимодействие организма со средой
Это и есть укорененность психики
Слайд 4НЕМНОГО ОБ EMBODIED COGNITION
Познание происходит:
в условиях дефицита времени,
в рамках конкретной ситуации.
Окружение

– часть когнитивной системы, снижающая нагрузку на нее.
Тесная связь познания и моторики.
Слайд 6PROBLEM SOLVING
А как обстоит дело с решением задач? Есть ли прямое участие

моторики в мыслительном процессе?
Инструментальная и функциональная роль моторики
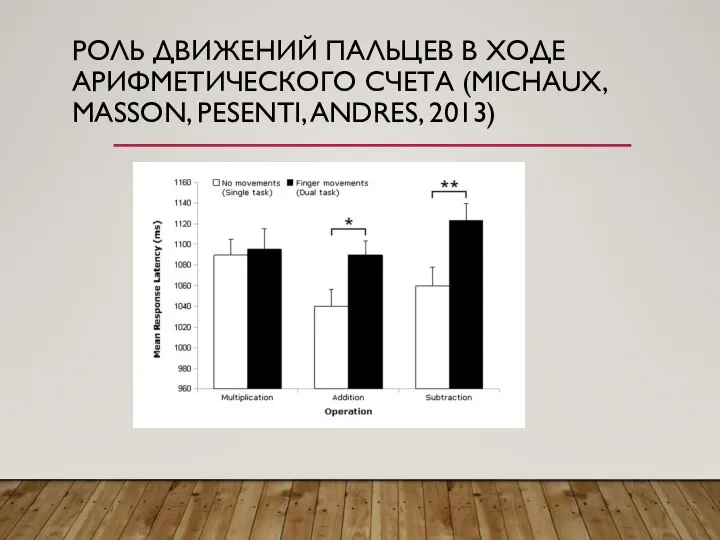
Слайд 7РОЛЬ ДВИЖЕНИЙ ПАЛЬЦЕВ В ХОДЕ АРИФМЕТИЧЕСКОГО СЧЕТА (MICHAUX, MASSON, PESENTI, ANDRES, 2013)

Слайд 8РОЛЬ ДВИЖЕНИЙ ПАЛЬЦЕВ В ХОДЕ АРИФМЕТИЧЕСКОГО СЧЕТА (MICHAUX, MASSON, PESENTI, ANDRES, 2013)
Слайд 9ТРЕНИРОВКА ДВИЖЕНИЯ РУК (WERNER, RAAB, 2013, EXP. 2)
Два типа движений руками –
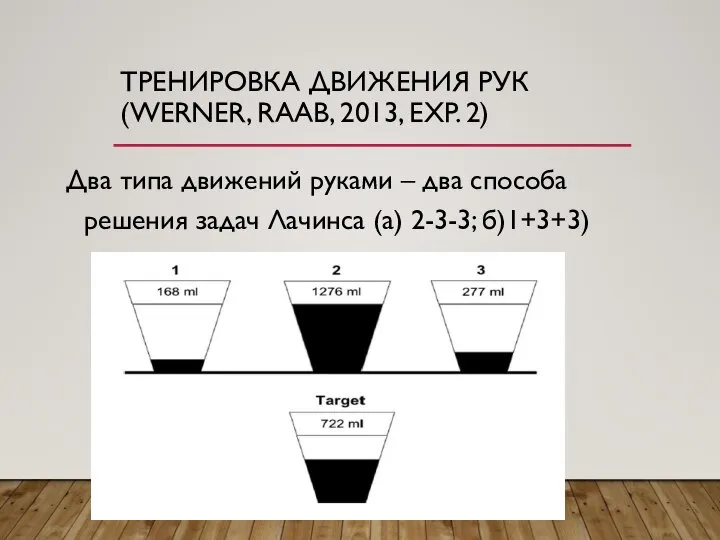
два способа решения задач Лачинса (а) 2-3-3; б)1+3+3)
Слайд 10
Оба раза обратим внимание на сложение и вычитание

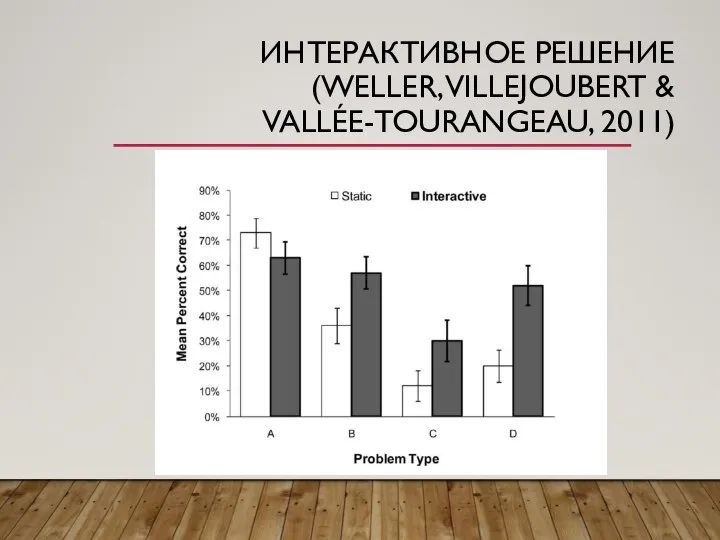
Слайд 12ИНТЕРАКТИВНОЕ РЕШЕНИЕ (WELLER, VILLEJOUBERT & VALLÉE-TOURANGEAU, 2011)
Слайд 13ПРОЦЕДУРА РЕПЛИКАЦИИ: ИНДИВИДУАЛЬНОЕ РЕШЕНИЕ 5 МИНУТ
4 экспериментальные группы:
Гр1: Решала, перекладывая карандаши руками
Гр2:

Решала, не трогая разложенные на столе карандаши
Гр3: Решала по фото
Гр4: Сначала выкладывала задание по фото, а потом решала, перекладывая карандаши руками
Слайд 14РЕПЛИКАЦИЯ: ПРИМЕР СТИМУЛЬНОГО МАТЕРИАЛА (ФОТО)

Слайд 15РЕПЛИКАЦИЯ
Независимая переменная:
условия решения
Зависимые переменные:
% правильных ответов; время решения задачи
Исп. №

3
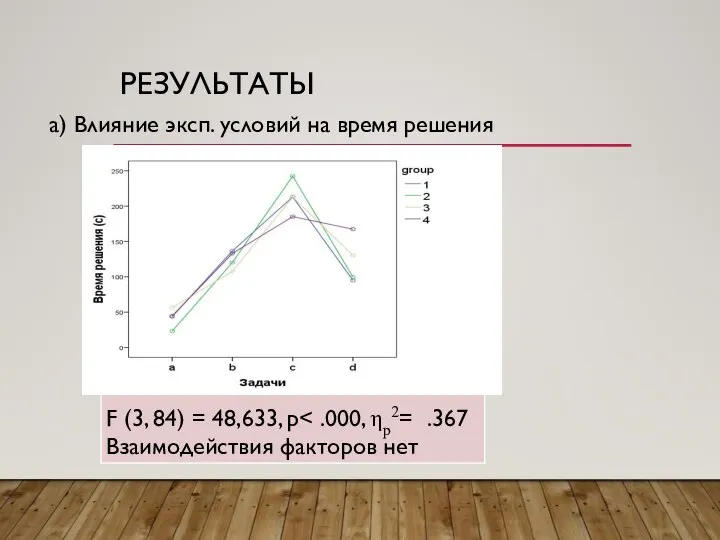
Слайд 16РЕЗУЛЬТАТЫ
а) Влияние эксп. условий на время решения
Слайд 17РЕЗУЛЬТАТЫ
б) Влияние эксп. условий на успешность решения
F (3, 84) = 28,09, p<
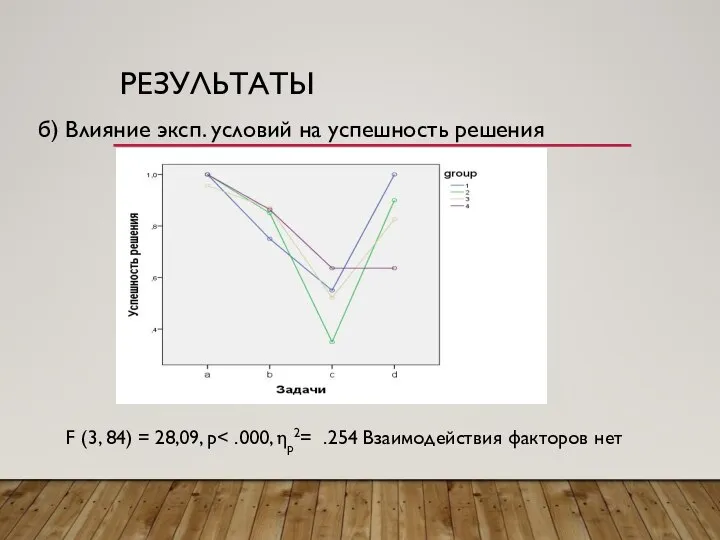
.000, ηp2= .254 Взаимодействия факторов нет
Слайд 19ОБРАТИМ ВНИМАНИЕ НА СТРУКТУРУ РЕЗУЛЬТАТОВ
Успешность решения задач:
A>B>C <= три типа ограничений
A>D

<= «рыхлые» и «жесткие» чанки
Слайд 21ЧТО ДОБАВЛЯЕТСЯ В СЛУЧАЕ «МОТОРНОГО» РЕШЕНИЯ?
Нет общего описания, что делают испытуемые в

ходе решения этих задач
Модифицируют знаки, чтобы изменить значения, под-чиняясь правилам арифметики и выясняя «правила игры». Происходит решение семантической задачи. Движения позволяют нам до некоторой степени увидеть этот процесс
Слайд 22ТРИ СИСТЕМЫ «СЕМАНТИЧЕСКИХ» ПРАВИЛ
Постоянные правила: Римские числа (роль V и X)
Правила арифметики
Ситуативные

правила: Правила переклады-вания карандашей, т.е. изменения знаков и их сочетаний. (Их еще нужно выяснить)
Слайд 23ДОПУЩЕНИЯ О СВЯЗКЕ
«ЗНАК» – «ЗНАЧЕНИЕ»
- Освоенная знаковая система – одинаковая доступность

всех знаков и операций с ними =
- То есть, одинаковая вероятность перемещения любых «разрешенных» карандашей.
Если это не так – то действуют какие-то когнитивные ограничения
Слайд 24Почему приходится анализировать семантику и когнитивные ограничения?
Потому что формальный анализ задач не

предсказывает ни их трудность для решения, ни характер этих трудностей
Слайд 25РАЗРЕШЕННЫЕ ПЕРЕМЕЩЕНИЯ (ВЕДУЩИЕ К НОВЫМ ЗНАЧЕНИЯМ БЕЗ НАРУШЕНИЯ ПРАВИЛ)
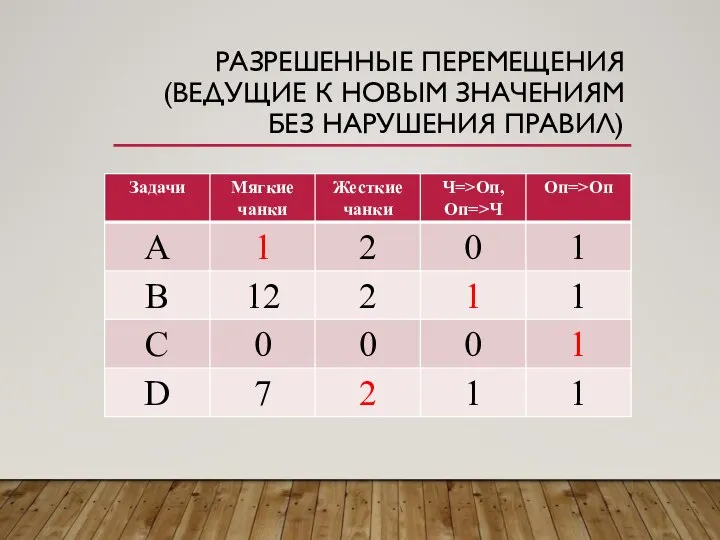
Слайд 26РАЗМЕТКА ВИДЕОПРОТОКОЛОВ
Перекладывание число -> число,
Перекладывание операция -> операция,
Перекладывание число <=>

операция,
Манипуляция числами,
Манипуляция операциями,
«Счет» руками,
Вопросы о правилах
«Эгоцентрическая речь»
Слайд 27ОТКЛОНЕНИЯ ОТ «ИДЕАЛА»
- Плохое знание римских чисел (про-пущенные или неразрешенные действия с

карандашами)
Роль жестких перцептивных чанков
Роль аффордансов (функциональные свойства карандашей)
Слайд 29ПРИМЕРЫ ОДНОВРЕМЕННОГО ИЗМЕНЕНИЯ
III = III + III
III = III – II

– I
Слайд 30МЕНТАЛЬНАЯ И «МОТОРНАЯ» АРИФМЕТИКА
«Внутренние» операции vs семантически «нагруженные» движения
А) Поисковые (исследовательские,

эпистемические) движения;
Б) «Решающие» движения
Слайд 31
«Грубость» зависимых переменных и всего последующего анализа

Слайд 32ЭПИСТЕМИЧЕСКАЯ АКТИВНОСТЬ
1) Вопросы о правилах
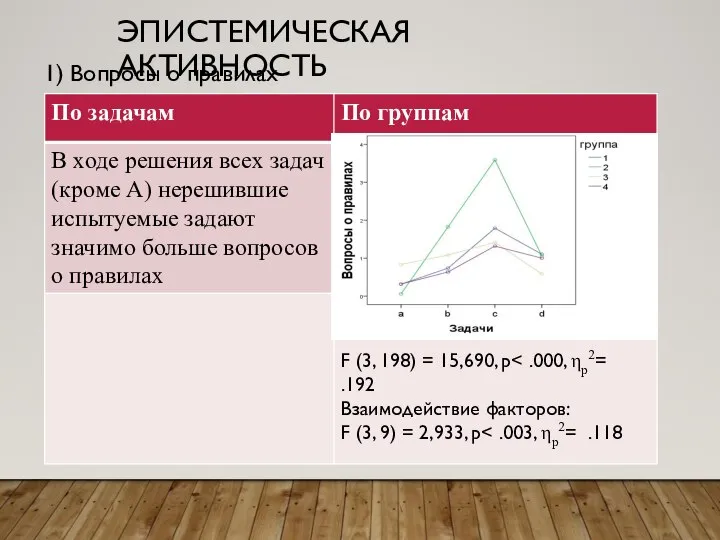
Слайд 33ЭПИСТЕМИЧЕСКАЯ АКТИВНОСТЬ
2) Эпистемические движения. (Предположим, что манипуляции карандашами это они и есть)
а)

«удельный вес»
- Перекладывание цифр значимо чаще, чем манипуляция ими (А и D);
- Перекладывание операций значимо реже, чем манипуляции ими (В и D)
Слайд 34ЭПИСТЕМИЧЕСКАЯ АКТИВНОСТЬ
б) Роль в успешном решении
Мы сравнили успешных и неуспешных решателей. Неуспешные

чаще: Манипулируют цифрами – задачи В и D
Манипулируют знаками – задача С
Общая мораль – отрицательная!
Слайд 35«РЕШАЮЩИЕ» ДВИЖЕНИЯ
Мы не знаем, что это такое. Откуда мы знаем, что они

вообще существуют?
Почти нет эффектов научения в ходе экспери-мента (Перемещение операций (B); Вопросы о правилах (А, B, D))
Суперрешатели (4 успеха) - практически не отличаются от всех прочих
Мораль опять отрицательная
Слайд 36«ВИШЕНКА НА ТОРТЕ»
Наши испытуемые понимают процесс решения этих задач классически – «сначала

решу «в голове», а потом переложу карандаш». Т.е. они не чувствуют позитивной роли моторики
Слайд 37ВЕРНЕМСЯ К РЕПЛИКАЦИИ
Каким образом моторика может помочь решать обсуждаемые задачи (особенно тип

С)?
Чанки, а что еще? Как реализуется «семантическая» нагрузка движения?
Кажется, что предшественники искали воплощен-ное познание в решении этих задач не там. И оно не может быть в них одинаковым
Слайд 38«РЕШАЮЩИЕ» ДВИЖЕНИЯ
Как это может выглядеть? Например, что-то типа свободных радикалов, имеющих пустые

валентности
Решатель поднимает рукой карандаш. И?
Репрезентация «семантической» цели: конкуренция возможных «новых» значений. Как мы видели, они бывают числовые, операциональные и более сложные.
Траектории движения глаз при поиске и выборе пустых «валентных» мест.
Сравнение новичков и экспертов
- Подсказки мест или конфигураций
Слайд 39ПРИМЕРЫ СВОБОДНЫХ РАДИКАЛОВ С ПУСТЫМИ ВАЛЕНТНОСТЯМИ
III = 0V0 +III
III = 0V0 +III

III = V0 + III
III = V + III
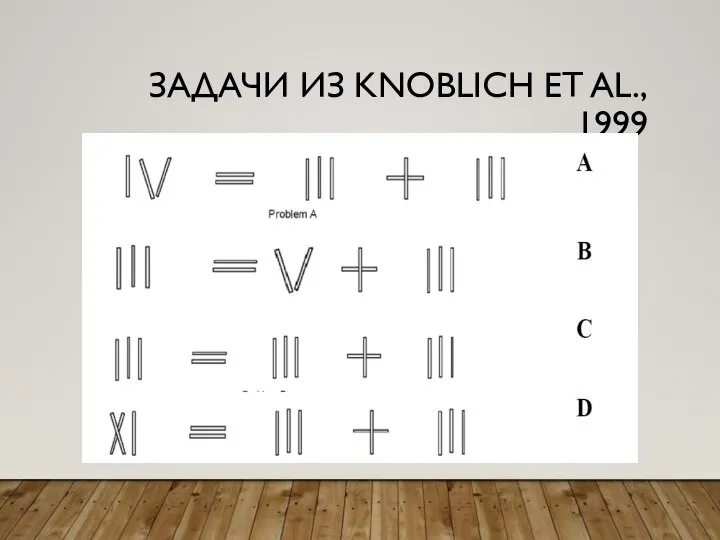
Слайд 41АНАЛИЗ ЗАДАЧ ИЗ KNOBLICH ET AL., 1999
«Мягкие», промежуточные и «жесткие» чанки







































 Составные условия в разветвляющихся алгоритмах © М.Е.Макарова http://www.uchinfo.com.ua http://www.uchinfo.com.ua. - презентация
Составные условия в разветвляющихся алгоритмах © М.Е.Макарова http://www.uchinfo.com.ua http://www.uchinfo.com.ua. - презентация Памятники Всемирного природного и культурного наследия
Памятники Всемирного природного и культурного наследия О КОМПАНИИ
О КОМПАНИИ Цели Формирование духового мира современной молодежи
Цели Формирование духового мира современной молодежи Birds
Birds Презентация на тему Франция после Первой Мировой Войны
Презентация на тему Франция после Первой Мировой Войны Шаблоны для уроков русский язык и литература 2
Шаблоны для уроков русский язык и литература 2 Компьютер и здоровье
Компьютер и здоровье Модели описания конфликта
Модели описания конфликта Развитие АСЦ Abat в РФ
Развитие АСЦ Abat в РФ Типы диагностических методик
Типы диагностических методик Олимпийские интеллектуальные игры
Олимпийские интеллектуальные игры Конкурс проектов lingua latina per se illustrata. Гуманитарный факультет
Конкурс проектов lingua latina per se illustrata. Гуманитарный факультет Perfect passive
Perfect passive Презентация на тему bmw
Презентация на тему bmw  Развитие птиц. Для детей
Развитие птиц. Для детей Характеристика фитнеса, как современного явления в физической культуре
Характеристика фитнеса, как современного явления в физической культуре Orientaciones generales Matrícula 2019-2020
Orientaciones generales Matrícula 2019-2020 Промышленное оборудование и комплексная автоматизация
Промышленное оборудование и комплексная автоматизация Животные Пермского края
Животные Пермского края Математика на службе армии (урок в 9 классе)
Математика на службе армии (урок в 9 классе) Проблема гендерного насилия в контексте гендерной политики в Германии
Проблема гендерного насилия в контексте гендерной политики в Германии Природа власти ее виды и источники
Природа власти ее виды и источники Что такое Хангыль ?
Что такое Хангыль ? Конструктивные решения промышленных зданий. Несущие и ограждающие конструкции промышленных зданий
Конструктивные решения промышленных зданий. Несущие и ограждающие конструкции промышленных зданий 10-13 апреля 2006 г. Украина, Киев Вторая международная выставка
10-13 апреля 2006 г. Украина, Киев Вторая международная выставка Русские ремесла. По трудовому обучению
Русские ремесла. По трудовому обучению Презентация на тему Школа безопасности
Презентация на тему Школа безопасности