Алгебра Логики

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Пример: «3 – простое число»
- является высказыванием, поскольку оно истинно.
Пример: «Давайте пойдем в кино»
- не является логическим высказыванием.
Логическое высказывание
Лекция 2: "Алгебра Логики"

Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Высказывательная форма
Пример. «x+2>5» – высказывательная форма, которая при x>3 является истинной, иначе ложной.
Лекция 2: "Алгебра Логики"

Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным.
Слова и словосочетания: «не», «и», «или», «если..., то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. .
Логические связки
Лекция 2: "Алгебра Логики"

Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными).
Высказывания, которые не являются составными, называются элементарными (простыми).
Логические связки
Пример. Высказывание «Число 6 делится на 2» - простое высказывание.
Высказывание «Число 6 делится на 2, и число 6 делится на 3» - составное высказывание, образованное из двух простых с помощью логической связки «и».
Лекция 2: "Алгебра Логики"

Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пример:
Обозначим через А простое высказывание
«число 6 делится на 2»,
а через В простое высказывание
«число 6 делится на 3».
Тогда составное высказывание:
«Число 6 делится на 2, и число 6 делится на 3»
можно записать как «А и В».
Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение
Лекция 2: "Алгебра Логики"

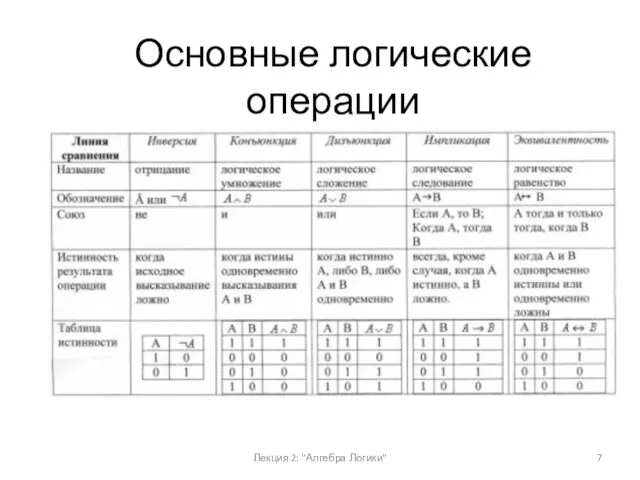
Лекция 2: "Алгебра Логики"
Основные логические операции

Лекция 2: "Алгебра Логики"
Таблицы истинности

Лекция 2: "Алгебра Логики"
Таблицы истинности
Определить количество строк:
– количество строк = 2n + строка для заголовка,
– n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
– определить количество переменных (простых выражений);
– определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Лекция 2: "Алгебра Логики"
Таблицы истинности
Пример.
Составить таблицу истинности для формулы И–НЕ, которую можно записать так: ¬(A&B) .
Определить количество строк:
На входе два простых высказывания: А и В, поэтому n=2 и количество строк =22+1=5.
2. Определить количество столбцов:
Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.
3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3).

Лекция 2: "Алгебра Логики"
Таблицы истинности
Подобным образом можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать так: ¬(A∨B) .

Лекция 2: "Алгебра Логики"
Логические формулы можно также представлять с помощью языка логических схем.
Существует три базовых логических элемента, которые реализуют три основные логические операции:
логический элемент «И» – логическое умножение – конъюнктор; логический элемент «ИЛИ» – логическое сложение – дизъюнктор; логический элемент «НЕ» – инверсию – инвертор.
Логические схемы

Лекция 2: "Алгебра Логики"
Алгоритм построения логических схем.
Определить число логических переменных.
2. Определить количество логических операций и их порядок.
3. Изобразить для каждой логической операции соответствующий ей логический элемент.
4. Соединить логические элементы в порядке выполнения логических операций.
Пример.
По заданной логической функции F(A,B)=¬A&B∨A&¬B построить логическую схему.
Решение.
Число логических переменных = 2 (A и B).
2. Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.
3. Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.
4. Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).