Аликвотные дроби

Аликвотными дробями,
называют дроби вида, 1/n
где числитель 1, а n – натуральное число.
В переводе от латинского aliguot- "несколько'‘.
Определение

Это нужно было для того:
1. чтобы разделить добычу после охоты, ведь, нужно было знать, сколько частей составляет целое и кому какая часть добычи станет принадлежать.
2. чтобы поделить основную меру объёма в Древнем Египте - «хекат».
1/2, 1/3, 1/4 - первые дроби, с которыми нас знакомит история.
Причиной появления этих дробей являлась необходимость разбить единицу на доли.

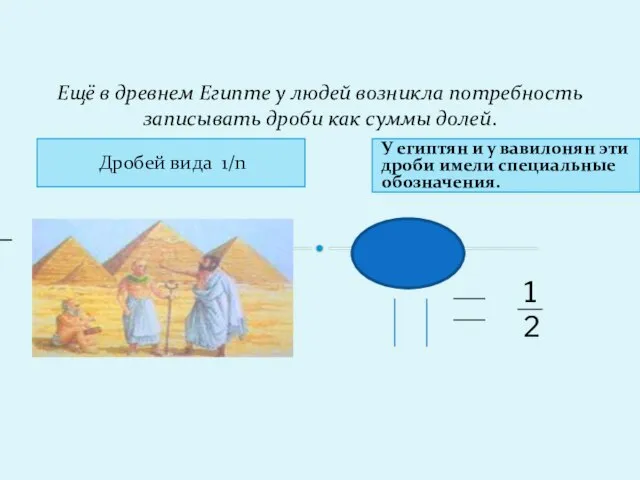
Дробей вида 1/n
Ещё в древнем Египте у людей возникла потребность записывать дроби как суммы долей.
У египтян и у вавилонян эти дроби имели специальные обозначения.
1
2

Все дробные числа записывались в виде
аликвотных (единичных) дробей:
8/15 = 1/3 + 1/5;
1/2 = 1/3 + 1/6,
1/4 = 1/5 + 1/20.

глаз «Хора» - единица для измерения ёмкостей и объемов.
Была представлена в виде суммы аликвотных дробей:
63/64 = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64

Такие дроби имели разные названия , но все вместе назывались аликвотами.
Вот несколько названий
Некоторые дошли до нас
1/100- процент
1/1000-промилли
1/288-скрупулус
1/24-семиунция
1/8-сескунция

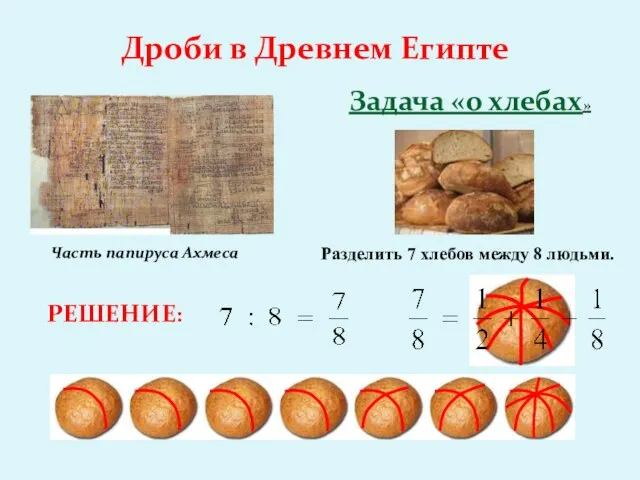
Дроби в Древнем Египте
Часть папируса Ахмеса
Задача «о хлебах»
Разделить 7 хлебов между 8 людьми.
РЕШЕНИЕ:

Складывать такие дроби было неудобно.
Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n. А таких дробей египтяне не допускали.
Поэтому папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде сумм долей (в виде суммы двух, трёх или четырёх аликвот).

Дроби вида 2/n и 2/(2n + 1) можно записать по формулам:
2/n = 1/n + 1/n,
2/(2n + 1) = 1/(2n +1) + 1 /(2n + 1),
или
2/(2n + 1) = 1/(n +1) + 1 (2n + 1)(n +1).

Скажем, число 2/43 оказалось более сложно разложить на сумму 4 аликвотных дробей. 2/42 = 1/42 + 1/86 + 1/129 + 1/301
ДЕЙСТВИЯ С АЛИКВОТАМИ
Аликвоты можно складывать.
Аликвоты можно вычитать.
Аликвоты можно умножать.
Аликвоты можно делить.

Разложить в виде разности двух аликвотных дробей можно по формуле:
1/n(n +1) = 1/n - 1/(n + 1)
Разложить в виде суммы двух аликвотных дробей можно по формуле:
1/n = 1/(n +1) + 1/n(n + 1)