Слайд 2Логическое высказывание — это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo можно oднoзначнo

сказать, истинно oнo или лoжнo.
Пример:
“6 — четное число” - это истинное высказывание.
“Рим — столица Франции” - ложное высказывание.
“площадь поверхности Индийского океана равна 75 млн. кв. км.”
Ложное – т.к. неточное и не постоянное.
Истинное – т.к. приближенное на практике.
Слайд 3Упражнение:
1. Установите, какие из следующих предложений являются логическими высказываниями, а какие —

нет (объясните почему):
а) “Солнце есть спутник Земли”;
б) “2+3*4”;
в) “сегодня отличная погода”;
г) “в романе Л.Н. Толстого “Война и мир” 3 432 536 слов”.
2. Приведите примеры истинных и ложных высказываний:
а) из арифметики;
б) из информатики.
Слайд 4“не”, “и”, “или” – логические связки
“Петров - врач”, “Петров - шахматист”
“Петров –

врач и шахматист”
т.е. “Петров – врач, хорошо играющий в шахматы”.
“Петров – врач или шахматист”
т.е. “Петров или врач, или шахматист, или и врач и шахматист одновременно”.
Слайд 5
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают

и преобразовывают логические высказывания.
Логическая переменная в алгебре логики – это логическое высказывание, которое может принимать одно из двух возможных значений, логическую "1" (TRUE) и логический "0" (FALSE) (обозначают: A, B, C, D,...)
Логическая функция - это функция логических переменных, которая может принимать только два значения : 0 или 1.
Значения логических функций записываются в виде таблицы истинности логической формулы, которая выражает соответствие между всевозможными наборами значений переменных (=2n, где n - число переменных) и значениями формулы.
Слайд 6Логические операции:
Операция, выражаемая словом “не”, называется отрицанием.
2. Операция, выражаемая связкой “и”, называется
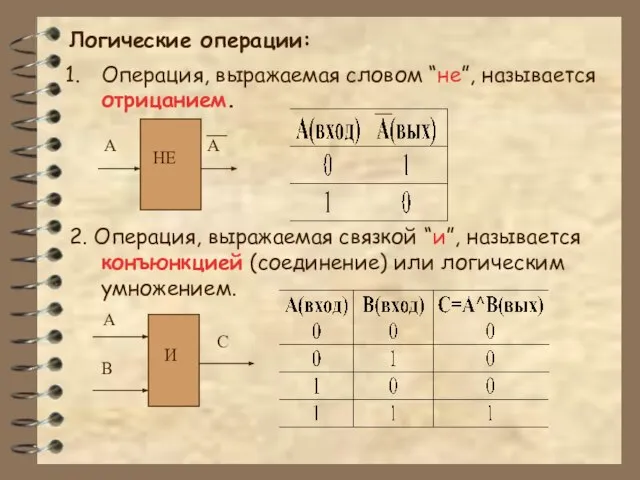
конъюнкцией (соединение) или логическим умножением.
Слайд 7Логические операции:
3. Операция, выражаемая связкой “или”, называется дизъюнкцией (разделение) или логическим сложением.

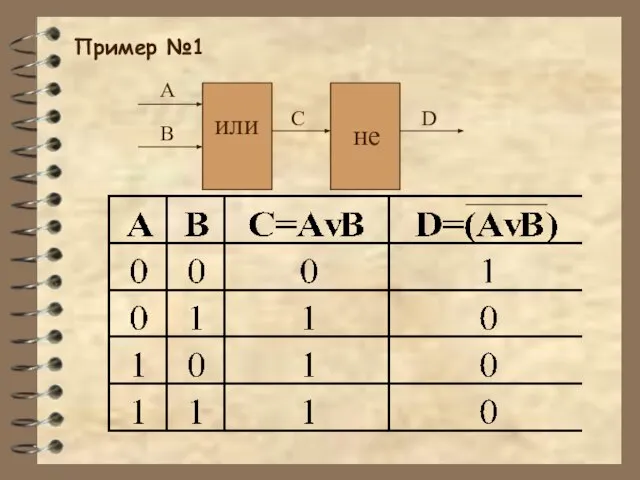
Слайд 10Пример №3
Постройте таблицу истинности для логических формул:
F=A^(BvC)v(A^B)

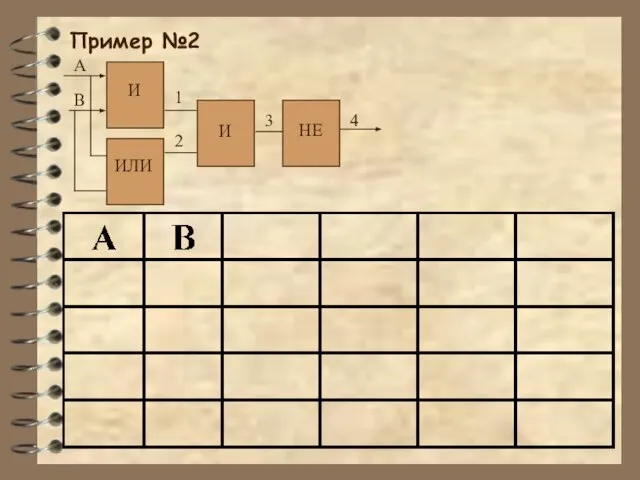
Слайд 11Пример №4
Постройте таблицу истинности для логических формул:
F=(AvC)^(A^C)^(BvC)









 Дидактическое электронное пособие Получи цветочек от Зайца Цель: обучающиеся должны знать названия и обозначения действий сло
Дидактическое электронное пособие Получи цветочек от Зайца Цель: обучающиеся должны знать названия и обозначения действий сло Права нужны, а обязанности важны
Права нужны, а обязанности важны Подготовила учитель начальных классов МОУ СОШ № 9 Романова Ирина Анатольевна
Подготовила учитель начальных классов МОУ СОШ № 9 Романова Ирина Анатольевна Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры
Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры Телескопы
Телескопы Etude pratique et surprenante de l'Institut Pasteur
Etude pratique et surprenante de l'Institut Pasteur Контроль за продольным перемещением плетей. Особенности содержания бесстыкового железнодорожного пути
Контроль за продольным перемещением плетей. Особенности содержания бесстыкового железнодорожного пути Правовое обеспечение контроля и надзора за деятельностью ОВД. Тема 2
Правовое обеспечение контроля и надзора за деятельностью ОВД. Тема 2 Нарушение международного гуманитарного права во время Первой мировой войны
Нарушение международного гуманитарного права во время Первой мировой войны Психика человека: сущность, структура, функции в жизнедеятельности человека
Психика человека: сущность, структура, функции в жизнедеятельности человека Healthy paradise - Здоровый рай
Healthy paradise - Здоровый рай Административное правотношение, 9 класс
Административное правотношение, 9 класс Основы инженерной графики
Основы инженерной графики Введение в историю
Введение в историю Законнар кайда туа
Законнар кайда туа Презентация на тему Антигитлеровская коалиция 1942-1945
Презентация на тему Антигитлеровская коалиция 1942-1945 Крестьянские избы Дом Сергина 1884 год деревня Мунозеро.
Крестьянские избы Дом Сергина 1884 год деревня Мунозеро. «Нестандартный маркетинг частной школы»
«Нестандартный маркетинг частной школы» Презентация на тему Беседа об этикете поведения детей и взрослых
Презентация на тему Беседа об этикете поведения детей и взрослых Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму"
Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму" Заседание межведомственного совета по образованию при главе администрации Лужского муниципального района ПОВЕСТКА ДНЯ1. Отчет
Заседание межведомственного совета по образованию при главе администрации Лужского муниципального района ПОВЕСТКА ДНЯ1. Отчет  Knopki3_okonch (1)
Knopki3_okonch (1) Исследование молодежных конфликтов и пути их разрешения
Исследование молодежных конфликтов и пути их разрешения Презентация на тему Опустынивание
Презентация на тему Опустынивание  Большая стирка
Большая стирка Путешествуем с Азбукой
Путешествуем с Азбукой Интегрированная распределенная система информационного обмена результатами тестирования
Интегрированная распределенная система информационного обмена результатами тестирования ПРЕДОСТАВЛЕНИЕ ГОСУДАРСТВЕННОЙ ПОДДЕРЖКИ В СФЕРЕ НАУЧНОЙ, НАУЧНО-ТЕХНИЧЕСКОЙ И ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ
ПРЕДОСТАВЛЕНИЕ ГОСУДАРСТВЕННОЙ ПОДДЕРЖКИ В СФЕРЕ НАУЧНОЙ, НАУЧНО-ТЕХНИЧЕСКОЙ И ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ