Алгоритм построения орграфа Хаффмана (алгоритм сжатия)

Давид Хаффман (1925-1999)
Давид начал свою научную карьеру студентом в Массачусетсом технологическом институте (MIT), где построил свои коды в начале пятидесятых годов прошлого века.

Закодируем предложение
«НА_ДВОРЕ_ТРАВА,_НА_ТРАВЕ_ДРОВА»
Вначале нужно подсчитать количество вхождений каждого символа в тексте.
Создаем первый узел
0
1
3

Создаем еще один узел
1
1
4
0
4
0
0
1
3
0
0
1
1
4
Создаем еще один узел
3

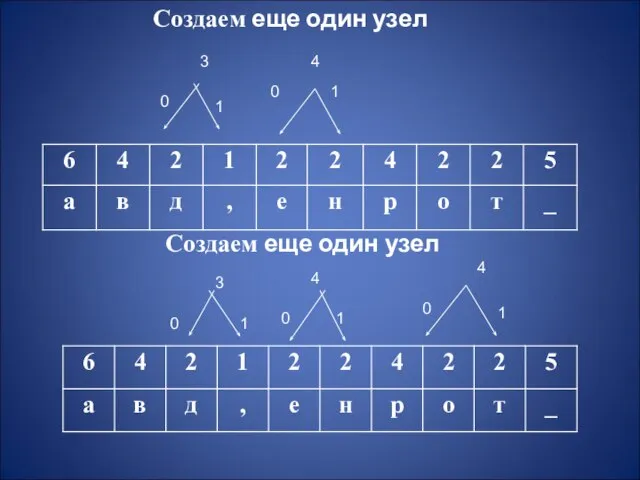
Создаем еще один узел
1
1
1
0
0
4
0
0
0
1
7
1
8
7
0
0
0
0
1
1
1
1
4
4
Создаем еще один узел

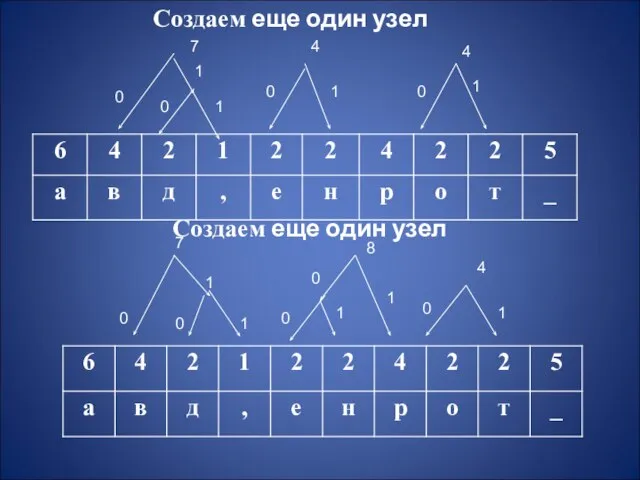
Создаем еще один узел
1
1
1
1
0
0
0
0
0
0
1
7
1
8
9

Создаем еще один узел
1
1
1
1
0
0
0
0
0
0
0
1
1
1
13
8
9

Создаем еще один узел
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
13
17

Создаем еще один узел
30
0
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1

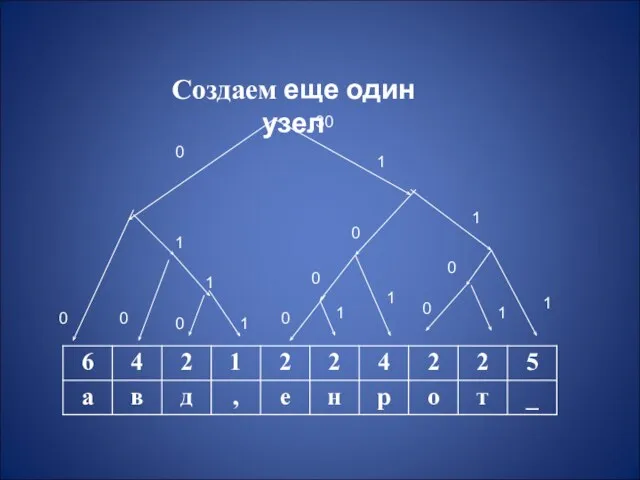
Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

ПОДСЧИТАЕМ, СКОЛЬКО ДВОИЧНЫХ СИМВОЛОВ ОКАЖЕТСЯ В СООБЩЕНИИ
«НА_ ДВОРЕ_ ТРАВА,_ НА_ ТРАВЕ_ ДРОВА»
ДЛЯ ЭТОГО НАДО НАЙТИ ПРОИЗВЕДЕНИЕ ЧИСЛА СИМВОЛОВ В КОДЕ КАЖДОЙ БУКВЫ НА КОЛИЧЕСТВО РАЗ, КОТОРОЕ ЭТА БУКВА ВСТРЕЧАЕТСЯ В СООБЩЕНИИ, А ЗАТЕМ ПОЛУЧЕННЫЕ ПРОИЗВЕДЕНИЯ СЛОЖИТЬ. ПОЛУЧАЕМ:
2*6+ 3*4+ 4*2+ 4*1+ 4*2+ 4*2 +3*4 +4*2 +4*2 +3*5 = 95

ПОСКОЛЬКУ В СООБЩЕНИИ ИСПОЛЬЗУЕТСЯ 10 РАЗЛИЧНЫХ СИМВОЛОВ, ДЛЯ ИХ КОДИРОВАНИЯ ТРЕБУЕТСЯ КАК МИНИМУМ ЧЕТЫРЕХБИТОВЫЕ ЦЕПОЧКИ, ПОЭТОМУ ПОСЛЕ КОДИРОВАНИЯ ДАННОГО СООБЩЕНИЯ ПОЛУЧИТСЯ ЦЕПОЧКА ОБЪЕМОМ 120 БИТ.
КОЭФФИЦИЕНТ СЖАТИЯ ЭТО ОТНОШЕНИЕ ОБЪЕМА ИСХОДНОГО СООБЩЕНИЯ К ОБЪЕМУ СЖАТОГО. В НАШЕМ СЛУЧАЕ ЭТО ОТНОШЕНИЕ РАВНО 120/95 = 120/95 = 1,26 .

НА САМОМ ДЕЛЕ ДАННОЕ СООБЩЕНИЕ В ПАМЯТИ КОМПЬЮТЕРА ЗАКОДИРОВАНО С ПОМОЩЬЮ ASCII, ПОЭТОМУ НА КАЖДЫЙ СИМВОЛ ОТВЕДЕНО 8 БИТ.
ТЕМ САМЫМ, ОБЪЕМ ИСХОДНОГО СООБЩЕНИЯ 240 БИТ, А КОЭФФИЦИЕНТ СЖАТИЯ СОСТАВЛЯЕТ 240/95 = 2,53.
ИЗ ЭТОГО ВИДНО, КАКОЙ ВЫИГРЫШ МЫ ПОЛУЧИЛИ, ЕСЛИ ЭТО СООБЩЕНИЕ НУЖНО БЫЛО БЫ ПЕРЕДАТЬ ПО КАНАЛУ СВЯЗИ ИЛИ СОХРАНИТЬ НА КАКОМ-ЛИБО НОСИТЕЛЕ.

ДЛЯ ДЕКОДИРОВНИЯ СЖАТОГО СООБЩЕНИЯ ВМЕСТЕ С НИМ ОБЫЧНО ПЕРЕСЫЛАЮТ НЕ КОДЫ ИСХОДНЫХ СИМВОЛОВ (Т.Е. ПЕРВЫЕ ДВЕ СТРОКИ), А САМ ОРГРАФ ХАФФМАНА (БЕЗ УКАЗАНИЯ ВЕСА КОРНЯ И РАЗМЕТКИ НА ДУГАХ, ИБО ОНА СТАНДАРТНА: ДУГА, ИДУЩАЯ ВЛЕВО, РАЗМЕЧАЕТСЯ -0, А ИДУЩАЯ ВПРАВО -1).
НА ЭТОМ, ОКАЗЫВАЕТСЯ, ТО ЖЕ МОЖНО СЭКОНОМИТЬ.
МАТЕМАТИКИ ДОКАЗАЛИ, ЧТО СРЕДИ АЛГОРИТМОВ КОДИРУЮЩИХ КАЖДЫЙ СИМВОЛ ПО ОТДЕЛЬНОСТИ И ЦЕЛЫМ КОЛИЧЕСТВОМ БИТ АЛГОРИТМ ХАФФМАНА ОБЕСПЕЧИВАЕТ НАИЛУЧШЕЕ СЖАТИЕ.