Слайд 2Анализ Уравнения МРА
А. t-тесты.
t-тесты как и в парном РА, но число

степеней свободы равно n-k.
Слайд 3Анализ Уравнения МРА
Б. Доверительные интервалы.
Как и в парном РА, но число

степеней свободы n-k.
Слайд 4Анализ Уравнения МРА
Коэффициент детерминации имеет ту же интерпретацию, что и

в ПРА. Но не может использоваться для сравнения качества уравнений с разным числом регрессоров.
Слайд 5Скорректированный коэффициент
детерминации .
При добавлении к уравнению регрессии еще одной объясняющей

переменной коэффициент детерминации R2 или увеличивается, или не меняет своего значения.
То есть, чем больше объясняющих переменных в уравнении, тем больше, вообще говоря, значение R2.
Слайд 6Из-за этого R2 нельзя использовать для сравнения качества уравнений с разным числом

объясняющих переменных.
Чтобы преодолеть этот недостаток R2, был введен скорректированный коэффициент детерминации:
Другое обозначение - это R2adj.
Слайд 7Интерпретация – как и R2.
В определенной степени использование R2adj более корректно для

сравнения качества регрессий с разным числом независимых переменных.
Хотя этот коэффициент тоже несовершенен.
Слайд 8Коэффициенты детерминации введены, чтобы оценивать качество модели регрессии. Чем больше их значение,

тем выше качество.
Но главным при оценке качества модели являются экономическая теория и здравый смысл.
Слайд 9Г. F-тест на качество оценивания.
(F-тест-1)
Гипотеза о качестве построенной модели регрессии формулируется

следующим образом:
H0: β2 =…= βk = 0
HА: не H0
(или: HА: хотя бы один коэффициент βj не равен нулю).
Слайд 10То есть проверяется гипотеза: является ли значимой совместная объясняющая способность k-1 независимых

переменных.
(Этот тест дополняет t-тесты, которые используются для проверки значимости объясняющих способностей отдельных переменных: H0: β2 = 0; H0: β3 = 0; …)
Слайд 11Схема проверки теста:
F-статистика = Fстат =
Fстат считается также и EXCELем.
Задаем α

- уровень значимости.
чсс = n-k.
Число ограничений на коэффициенты k-1.
Слайд 12По таблице распределения Фишера находим Fкритическое = Fкр(k-1; n-k; α).
Если Fстат >

Fкритическое , гипотеза H0 отвергается при уровне значимости α.
Если Fстат < Fкритическое , гипотеза H0 не отвергается при уровне значимости α.











 Учитель информатики в моем представлении
Учитель информатики в моем представлении Топливный элемент: проблемы и перспективы
Топливный элемент: проблемы и перспективы Овощи. Приготовление блюд из овощей
Овощи. Приготовление блюд из овощей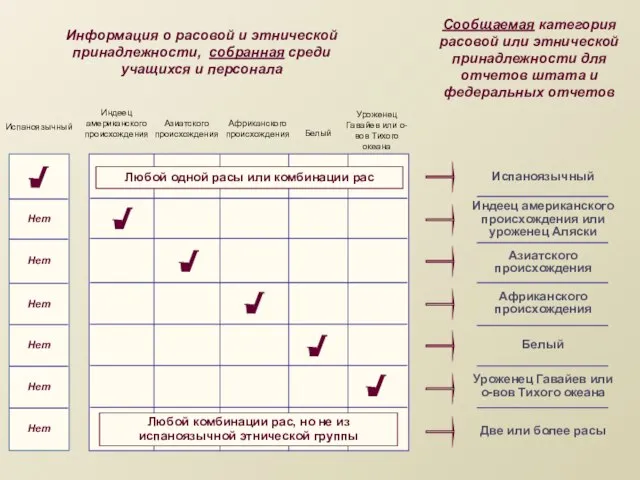 Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала
Информация о расовой и этнической принадлежности, собранная среди учащихся и персонала Возможности интернета в развитии интеллектуального потенциала старшеклассников
Возможности интернета в развитии интеллектуального потенциала старшеклассников Тоталитарное государство
Тоталитарное государство Морской лев
Морской лев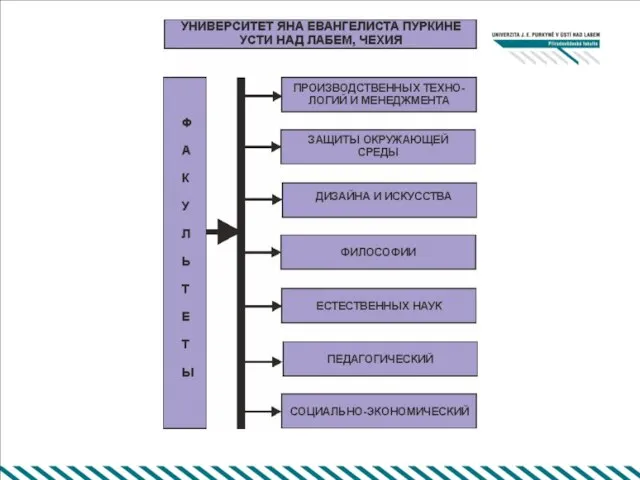 Университет Я. Э. Пуркине Факультет естественных наук Основан 4 ноября 2005 года. Цель факультета - подготовка бакалавров, магистров и
Университет Я. Э. Пуркине Факультет естественных наук Основан 4 ноября 2005 года. Цель факультета - подготовка бакалавров, магистров и Принципы и функции налогообложения
Принципы и функции налогообложения Технологическая карта
Технологическая карта Пульт горочный ПГУ-65
Пульт горочный ПГУ-65 ОАО «Российский банк развития»
ОАО «Российский банк развития» Сравнение скриптов TEMS
Сравнение скриптов TEMS Энергетика: вчера, сегодня, завтра
Энергетика: вчера, сегодня, завтра Житие Бориса и Глеба
Житие Бориса и Глеба Техника классического лыжного хода
Техника классического лыжного хода Салават Юлаев - национальный герой башкирского народа
Салават Юлаев - национальный герой башкирского народа ГРЕЙДИНГ
ГРЕЙДИНГ Основы православной культуры
Основы православной культуры Моя семья. Фотоальбом Артёма Тарасевича
Моя семья. Фотоальбом Артёма Тарасевича Методика Построение заборчика. Диагностика наглядно-действенного мышления у дошкольников
Методика Построение заборчика. Диагностика наглядно-действенного мышления у дошкольников Химические средства гигиены и косметики
Химические средства гигиены и косметики Колоноскопия и ирригоскопия. Виртуальная колоноскопия
Колоноскопия и ирригоскопия. Виртуальная колоноскопия Как пройти путь от создания идеи до действующего стартапа
Как пройти путь от создания идеи до действующего стартапа Презентація проекту“Порівняльний аналіз подій, що відбулися 150 років тому:1) 19 лютого(3 березня) 1861 р. цар Олександр ІІ видав маніф
Презентація проекту“Порівняльний аналіз подій, що відбулися 150 років тому:1) 19 лютого(3 березня) 1861 р. цар Олександр ІІ видав маніф Пантелеймон Куліш
Пантелеймон Куліш МЕЖДУНАРОДНЫЙ НАЛОГОВЫЙ КОНГРЕСС Заемное финансирование – практические аспекты Контролируемая задолженность: понятие и сложн
МЕЖДУНАРОДНЫЙ НАЛОГОВЫЙ КОНГРЕСС Заемное финансирование – практические аспекты Контролируемая задолженность: понятие и сложн Планирование и управление временем
Планирование и управление временем