Содержание
Слайд 289
та n = 0, ±1, ± 2,.... Будем полагать, что f (n)
89
та n = 0, ±1, ± 2,.... Будем полагать, что f (n)

f (n ± N) = f (n) для ∀ n.
(8.1)
Дискретное преобразование Фурье от функции f (n) определяется известной формулой
~
N −1
n=0
F[ f ] = f (k) = ∑ exp(i N kn) f (n);
2π
k = 0, N −1 ,
(8.2)
~
~
где, очевидно, Фурье-трансформанта f (k) - также периодическая функция с периодом N.
Если мы знаем Фурье-трансформанту f (k) , то мы можем восстановить
f (n), используя обратное дискретное преобразование
исходную функцию Фурье
−1
~
exp(−
1
~
N −1
k =0
N ∑
F [ f ] = f (n) =
2π
i kn) f (k); n = 0, N −1 .
N
(8.3)
В общем случае, число арифметических операций, которое требуется для вычисления дискретного преобразования Фурье, без затрат на вычисление
N
функций вида exp(i 2π kn) , оценивается формулой
TF ~ N 2 .
(8.4)
Для уменьшения числа операций, необходимых для вычисления преобра- зования Фурье, опишем алгоритм быстрого дискретного преобразования Фурье (БПФ). Положим N = N1 N2 , где N1 и N2 - целые числа. Представим k и n в
выражении (2) в виде k = k2 + k1N2 и n = n1 + n2 N1, где k1, n1 = 0, N1 −1;
~ ~
k2 , n2 = 0, N2 −1. Тогда из (2) получим
f (k) = f (k1, k2 ) ==
⎠
∑
N1 −1 N 2 −1
n1 =0 n2 =0 ⎝ 1 2
∑ exp ⎜i N N (k2 + k1N2 ) (n1 + n2 N1)⎟ f (n1,n2 ) =
⎛ 2π ⎞
⎠
⎞
1 2
1 1
N1−1
∑
n1=0 ⎝ 1
⎞ N2 −1
⎠ n2 =0 ⎝ 2
N N
N
exp ⎜i k n + i
⎛ 2π
2π
⎛ 2π
k2 n1 ⎟ ∑ exp ⎜i N k2 n2 )⎟ f (n1,n2 ).(8.5)
Слайд 390
Пусть N1 - простое число. Из (5) очевидно, что число арифметических операций,
90
Пусть N1 - простое число. Из (5) очевидно, что число арифметических операций,

Фурье, без затрат на вычисление функций exp(i
2π
N
kn) , оценивается форму-
лой
TF (N ) ~ N2 N 2 + N T (N ) .
1 1 F 2
(8.6)
Перепишем (6) в следующем виде
1
N
TF (N ) ~ N + TF (N2 ) .
(8.7)
N2
как произведение простых сомножителей числа
Представим N
N1, N2 ,..., Nm , т.е.
1 2 m
N = Nl1 Nl2 ...N lm .
(8.8)
Введем понятие целочисленного логарифма целого числа, как сумму всех про- стых сомножителей с учетом их кратности, т.е.
m
(8.9)
LOG(N ) = ∑lk Nk .
k =1
Отметим, что если N – простое число, то LOG(N ) = N .
Тогда из (7)-(9), получим, что число арифметических операций для вы- числения Фурье-преобразования (5) с использованием «быстрых» алгоритмов оценивается формулой
TFF
~ N LOG(N ) .
(8.10)
Если число N – представляется степенью двойки, то получаем хорошо извест- ную оценку для БПФ
~ N log 2 (N ) .
(8.11)
TFF
Рассмотрим матрицу следующего вида
Слайд 491
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎜− − − − − − − − − − − −
91
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎜− − − − − − − − − − − −

a1 a2 a3 ... a0
⎛ a0 a1 a2 ...
a0 a1 ...
aN −1 a0 ...
A = ⎜ aN −2
⎜
⎜ aN −1
aN −1 aN −2 aN −3
⎟.
(8.12)
Матрица вида (12) называется циркулянтной матрицей.
Будем рассматривать умножение матрицы (12) на N-мерный вектор u ,
v = Au .
(8.13)
Введем периодическую функцию дискретного аргумента A(n) и положим
A(−n) = an , n = 0, N −1. Тогда (13) можно переписать в следующем виде
N −1
v(n) = ∑ A(n − m) u(m),
n = 0, N −1.
(8.14)
m=0
Применим дискретное преобразование Фурье к обеим частям соотношения (14). Тогда для правой части получим
⎠
⎞
⎝
⎤
N −1 N −1
⎦ n=0 m=0
⎣m=0
⎢ ∑ A(n − m) u(m)⎥ = ∑ ∑ exp⎜i N kn⎟ A(n − m)u(m) =
F ⎡N −1
⎛ 2π
∑
∑
⎤
⎢ ⎥
⎡
⎟
⎞
⎜
⎝ ⎠ ⎣ ⎦
⎛
N −1
N −1
m=0 n=0
k(n − m) A(n − m)
km u(m) exp i
N N
exp i
2π
2π
. (8.15)
Рассмотрим вторую сумму в последнем выражении (15). Обозначая q=n-m, имеем
∑
⎟
⎠
⎞
∑ ⎜
⎝
⎛
⎤
⎥⎦
⎢⎣
⎡
N −1
N −1−m
n=0 q=−m
kq A(q)
N
exp i
A(n − m) =
k(n − m)
N
exp i
2π
2π
.
Далее, принимая во внимание периодичность функций
⎟
⎠
⎜
⎝
⎠
⎜ ⎟
⎝
N
N
A(q + N) = A(q), exp⎛i 2π k(q + N )⎞ = exp⎛i 2π kq⎞
получаем
 Всё про Деда Мороза и Новый год
Всё про Деда Мороза и Новый год Быт и обычаи в 18 веке
Быт и обычаи в 18 веке Построение аксонометрических плоскогранных фигур
Построение аксонометрических плоскогранных фигур Задачи развития Байкал-центра и СМУ
Задачи развития Байкал-центра и СМУ Компьютер в работе гуманитария
Компьютер в работе гуманитария Market Boro located under the railways station London
Market Boro located under the railways station London Коммуникационная политика на предприятии
Коммуникационная политика на предприятии  Révision. Lexique et grammaire. Французский язык
Révision. Lexique et grammaire. Французский язык Тайны русского языка
Тайны русского языка Простые механизмы. Рычаг
Простые механизмы. Рычаг Устное народное творчество. Малые жанры фольклора
Устное народное творчество. Малые жанры фольклора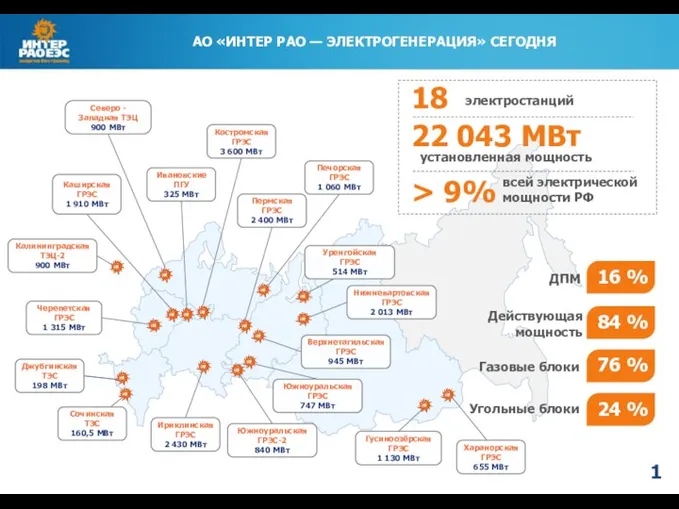 АО Интер РАО — электрогенерация сегодня
АО Интер РАО — электрогенерация сегодня Величайшая наука — математика
Величайшая наука — математика Презентация на тему Загадочная Намибия Племя Химба
Презентация на тему Загадочная Намибия Племя Химба  Презентация
Презентация Курсовой проект на тему «Разработка программного обеспечения УМК Экология 3»
Курсовой проект на тему «Разработка программного обеспечения УМК Экология 3» Презентация на тему Культурные растения
Презентация на тему Культурные растения  Риски предпринимательской деятельности
Риски предпринимательской деятельности Муравей – это студия семейного и детского творчества
Муравей – это студия семейного и детского творчества PH TaganrogFakultat fur FremdsprachenLehrstuhl fur Deutschprasentieren
PH TaganrogFakultat fur FremdsprachenLehrstuhl fur Deutschprasentieren Библия и Евангелие
Библия и Евангелие Виды гравировки. Настенные часы с индивидуальной гравировкой
Виды гравировки. Настенные часы с индивидуальной гравировкой Презентация на тему Чудотворные иконы России
Презентация на тему Чудотворные иконы России Футбол
Футбол Новые подходы в определении государственной и муниципальной службы. Предмет и границы государственной и муниципальной службы
Новые подходы в определении государственной и муниципальной службы. Предмет и границы государственной и муниципальной службы Персональные данные на сайтах государственных и муниципальных органов власти: проблемы и перспективы законодательства и правоп
Персональные данные на сайтах государственных и муниципальных органов власти: проблемы и перспективы законодательства и правоп Происхождение человека и становление общества
Происхождение человека и становление общества Понятие избирательной системы
Понятие избирательной системы