Слайд 2Быстрое преобразование Фурье
Основной принцип всех этих алгоритмов заключается в разложении операций вычисления

ДПФ сигнала длины на вычисление преобразований Фурье с меньшим числом точек. Разделив анализируемый набор отсчетов на части, вычисляют их ДПФ и объединяют результаты. Такие процедуры получили название алгоритмов быстрого преобразования Фурье БПФ.
При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления последовательности отсчетов на части (прореживание по времени или по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).
Слайд 3Быстрое преобразование Фурье
Рассмотрим алгоритмы БПФ с основанием 2, когда длина последовательности

, где целое число.
БПФ с прореживанием по времени. Рассмотрим идею БПФ с прореживанием по времени на примере деления набора отсчетов пополам. Введя общепринятое в литературе обозначение для дискретных экспоненциальных функций:
Запишем ДПФ сигнала в виде:
Слайд 4Быстрое преобразование Фурье
Разобьем на две -точечные последовательности, состоящие из отсчетов с четными

и нечетными номерами соответственно. В результате получим:
Заменяя индексы суммирования на при четном и на
при нечетном , придем к выражению:
Слайд 5Быстрое преобразование Фурье
Так как , то предыдущее выражение можно записать в виде:
(12.1)
Каждая

из сумм (12.1) является точечным ДПФ: первая – для четных отсчетов исходной последовательности, а вторая – для нечетных. Несмотря на то, что индекс в формуле (12.1) распространяется на значений , каждая из сумм требует вычислений только для , так как и
периодичны по с периодом . Объединение же этих сумм приводит к точечному ДПФ .
Слайд 6Быстрое преобразование Фурье
Схема БПФ
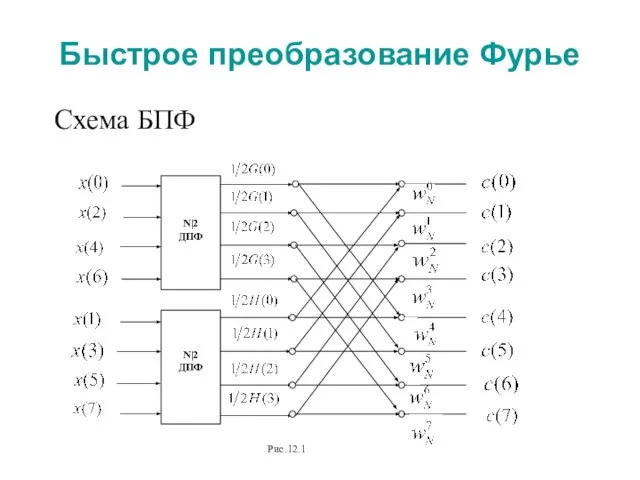
Слайд 7Быстрое преобразование Фурье
Далее можно вычислить каждое точечное ДПФ разбиением сумм на два

точечных ДПФ. Таким образом, и могут быть вычислены в виде:
Слайд 8Быстрое преобразование Фурье
Продолжим описанную процедуру разбиения исходной ДПФ на преобразования меньшей размерности,

пока не останутся только двухточечные преобразования. Двухточечные ДПФ (их число равно ) могут быть вообще вычислены без использования операций умножения. Действительно, для двухточечной последовательности согласно определению ДПФ имеем два спектральных отсчета:
Слайд 9Быстрое преобразование Фурье
Число требуемых при этом пар операций «умножение – сложение» можно

оценить как . Таким образом, вычислительные затраты по сравнению с непосредственным использованием формулы ДПФ уменьшается в раз. При больших это отношение становится весьма велико. Например, при
достигается более чем 100-кратное ускорение, но и это еще не предел. Количество комплексных умножений в алгоритме БПФ с прореживанием по времени может быть сокращено вдвое.
Слайд 10Быстрое преобразование Фурье
Из рассмотренного алгоритма следует, что на каждой ступени вычислений происходит

преобразование одного множества из комплексных чисел в другое множество из комплексных чисел.
Будем считать входным массивом на ступени вычисления , а – выходным массивом на ступени вычислений.
С учетом введенных обозначений имеем:









 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края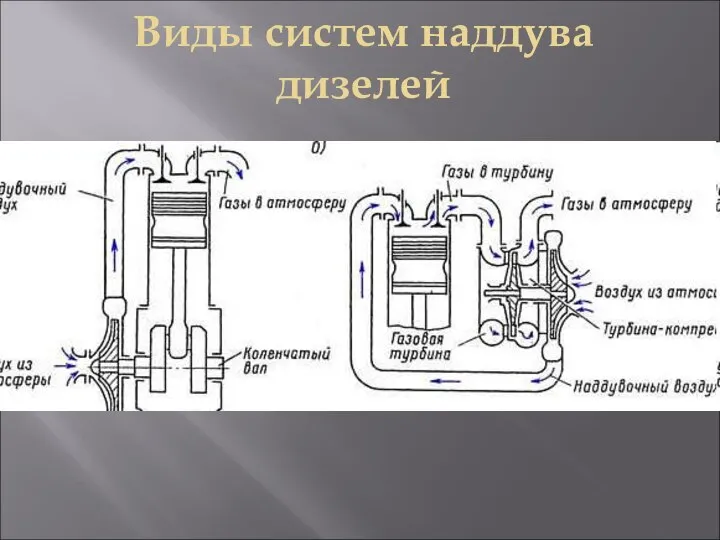 Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной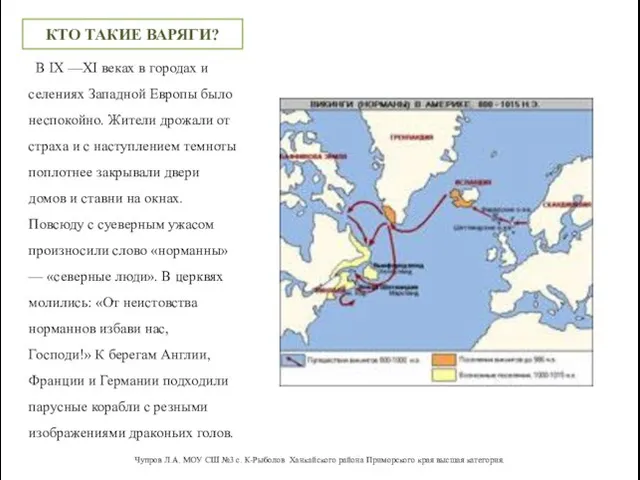 Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота