ЧИСЛЕННОЕ КОНФОРМНОЕ ОТОБРАЖЕНИЕ В ДВУМЕРНОЙ ГИДРОДИНАМИКЕ И СМЕЖНЫЕ ПРОБЛЕМЫ ЭЛЕКТРОДИНАМИКИ И ТЕОРИИ УПРУГОСТИ
Содержание
- 2. Доклад является представлением одноименной монографии Б.И. Рабиновича и Ю.В. Тюрина, выходящей в ИКИ на английском языке
- 3. NUMERICAL METHODS IN FLUID MECHANICS Boris I. Rabinovich and Yuri V. Tyurin Numerical Conformal Mapping in
- 4. Numerical Conformal Mapping in Two-Dimensional Hydrodynamics & Related Problems of Electrodynamics and Elasticity Theory by Boris
- 5. Acknowledgements The authors take this opportunity to express deep gratitude to their colleagues mentioned above for
- 6. Chapter 1 Lavrentiev Variational Principle and Auxiliary Transformations Lavrentiev variational principle and representation of mapping functions
- 7. Chapter 2 RT-Algorithm for Conformal Mapping of an Arbitrary Domain onto the Unit Circle and of
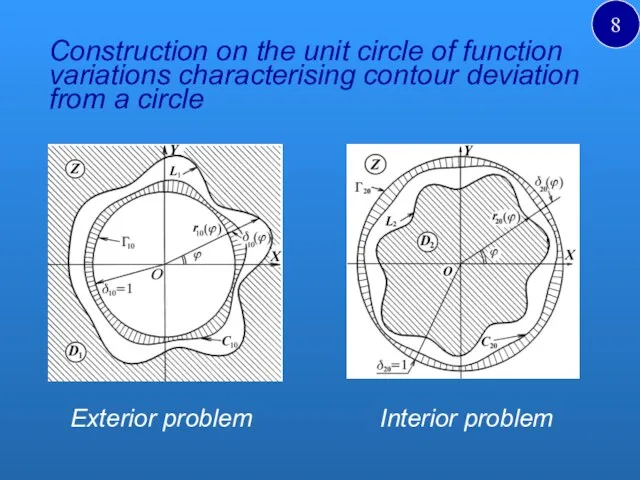
- 8. Construction on the unit circle of function variations characterising contour deviation from a circle Interior problem
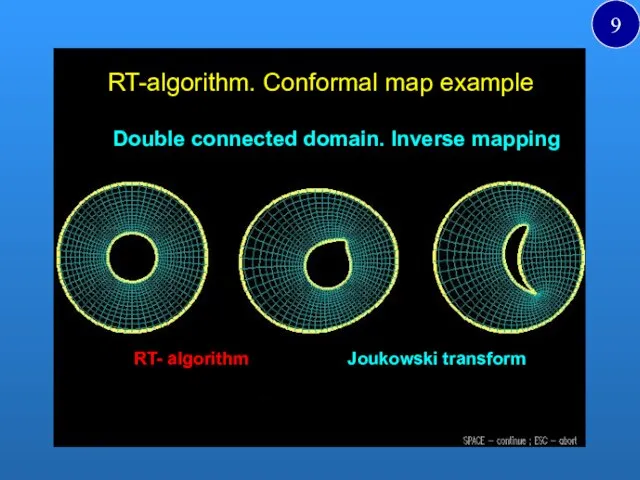
- 9. RT-algorithm. Conformal map example Double connected domain. Inverse mapping Joukowski transform RT- algorithm a 9
- 10. Chapter 3 Exterior problems of Hydrodynamics Two-dimensional flow problems: Complex potential and formulas of Blasius-Chaplygin and
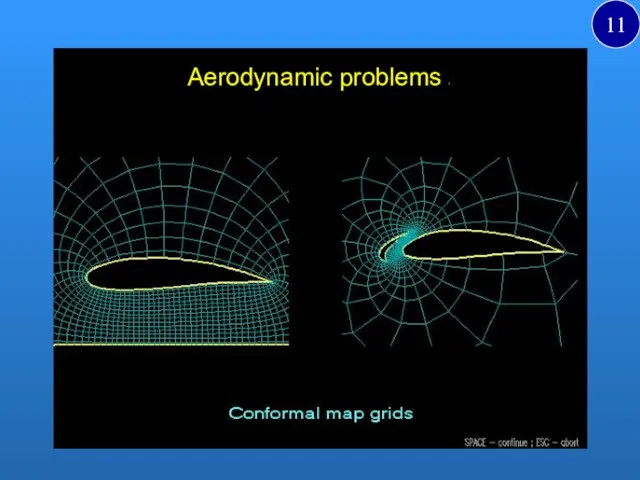
- 11. Aerodynamic problems 11
- 12. Potential Flow with two Vortices around the Arc Hydrodynamic problem 12
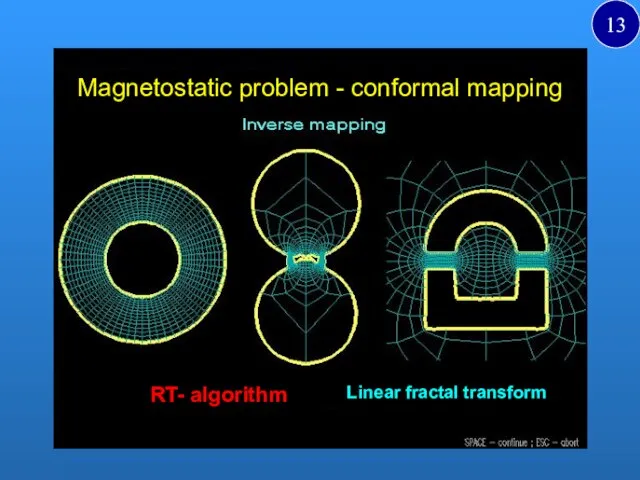
- 13. Magnetostatic problem - conformal mapping RT- algorithm Linear fractal transform 13
- 14. Chapter 4 Interior problems of Hydrodynamics Stokes-Joukowski problem. Interior boundary-value problems of fluid dynamics for moving
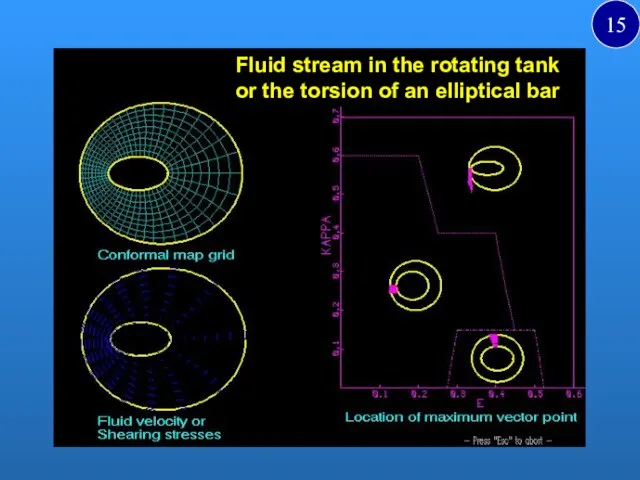
- 15. Fluid stream in the rotating tank or the torsion of an elliptical bar A 15
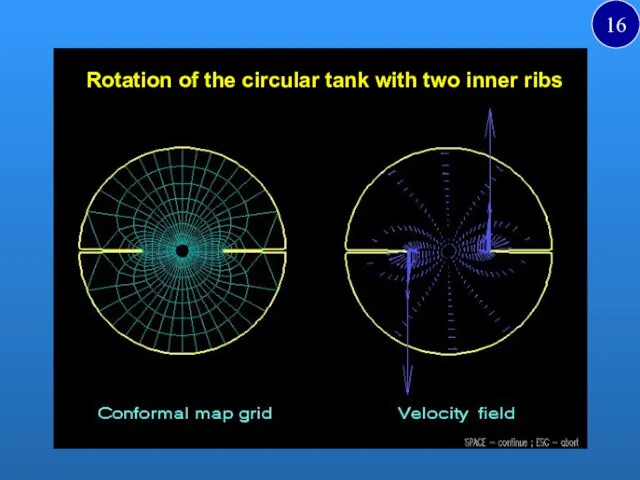
- 16. Rotation of the circular tank with two inner ribs 16
- 17. Without Vortices With Vortices Rotation of the circular tank with two inner ribs Stream lines 17
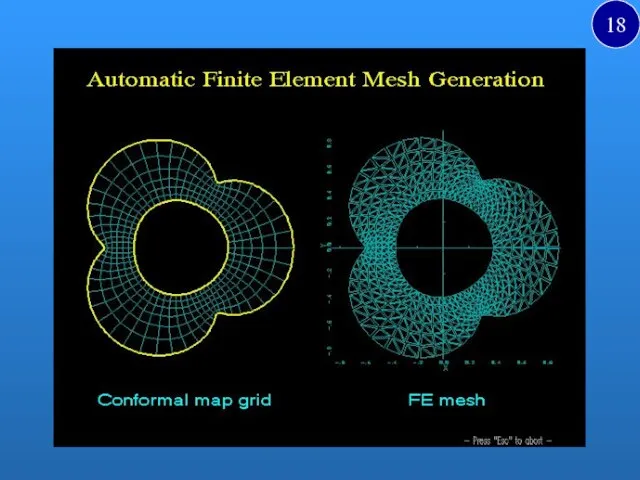
- 18. 18
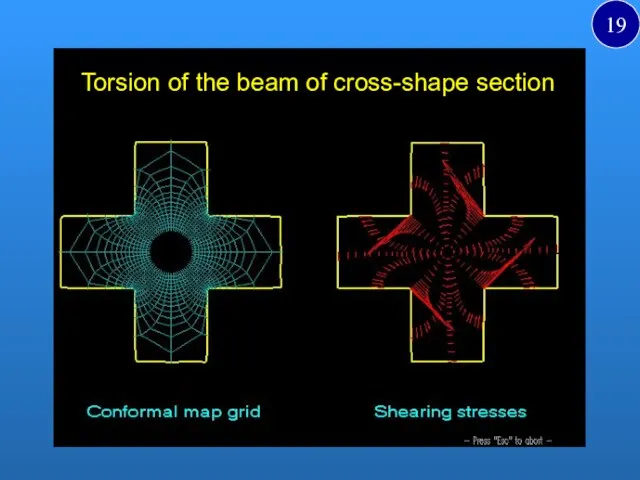
- 19. Torsion of the beam of cross-shape section 19
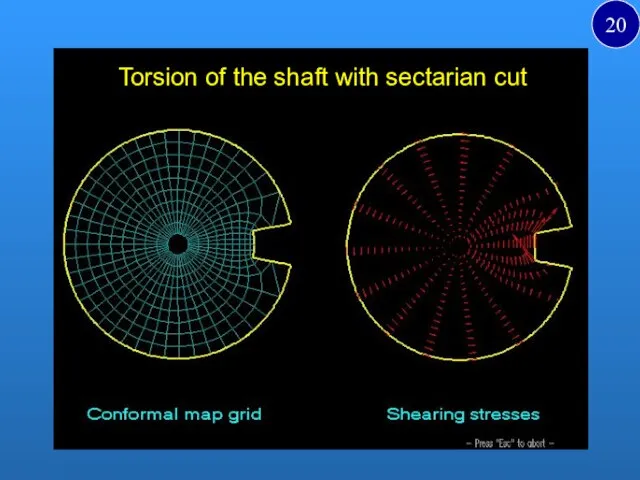
- 20. Torsion of the shaft with sectarian cut 20
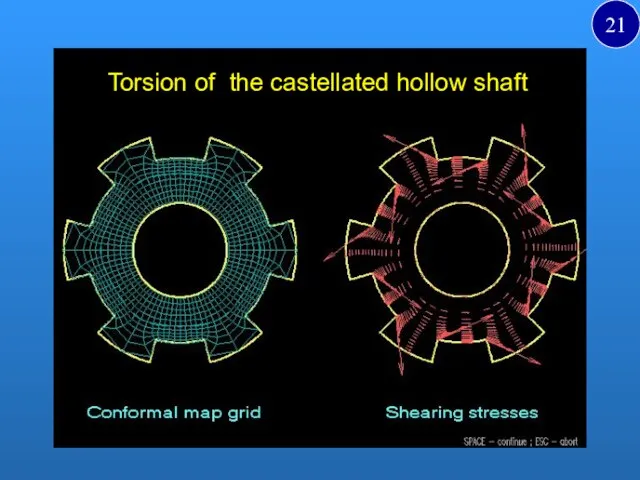
- 21. Torsion of the castellated hollow shaft 21
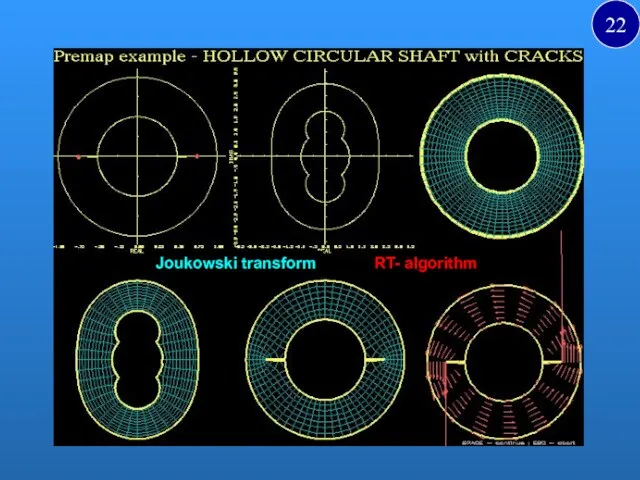
- 22. RT- algorithm Joukowski transform 22
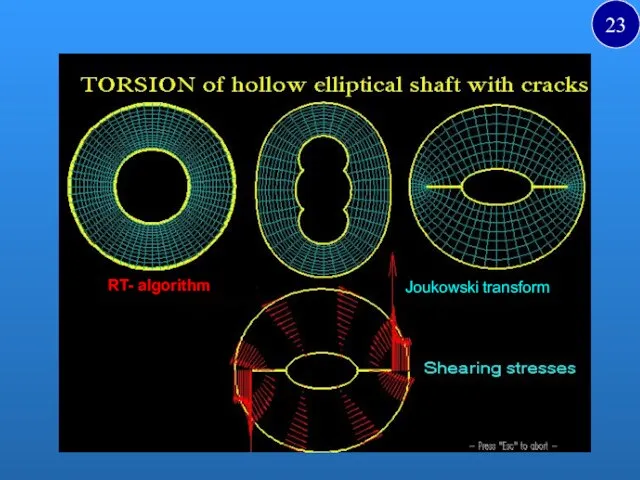
- 23. RT- algorithm Joukowski transform 23
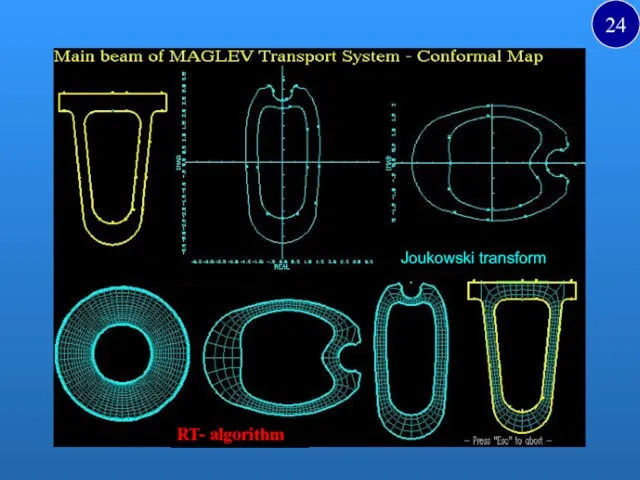
- 24. Joukowski transform RT- algorithm algorithm 24
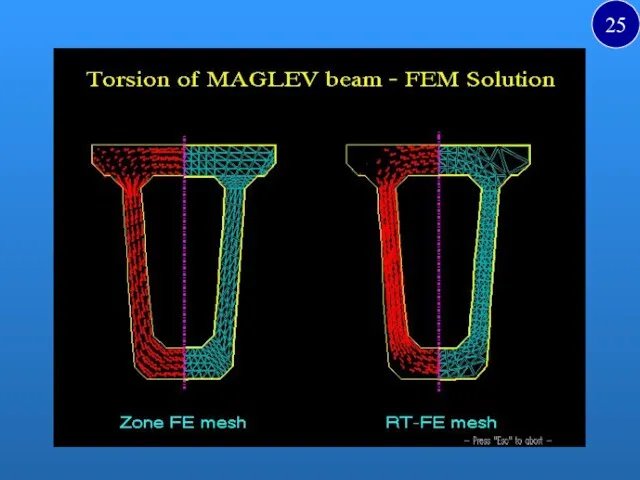
- 25. 25
- 26. 26
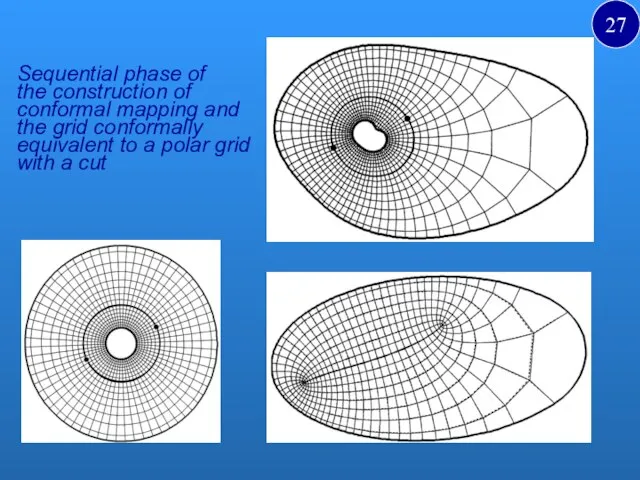
- 27. Sequential phase of the construction of conformal mapping and the grid conformally equivalent to a polar
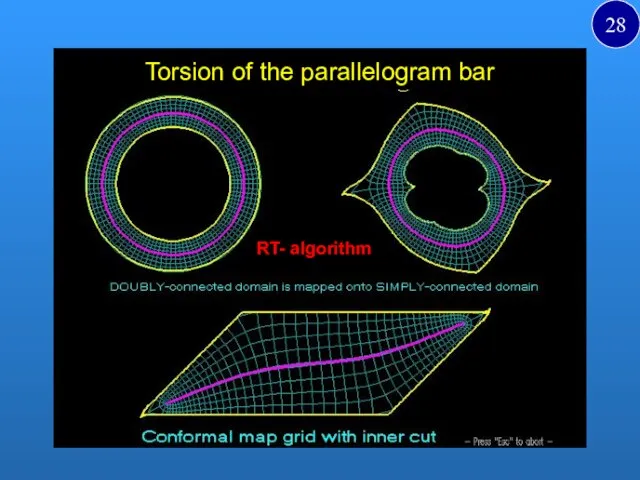
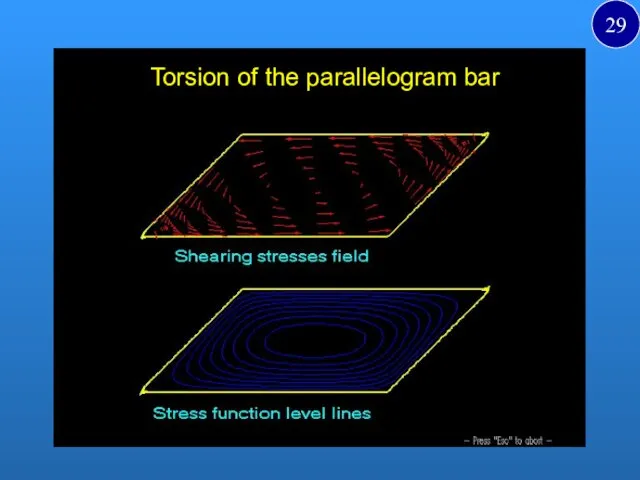
- 28. Torsion of the parallelogram bar RT- algorithm a 28
- 29. Torsion of the parallelogram bar 29
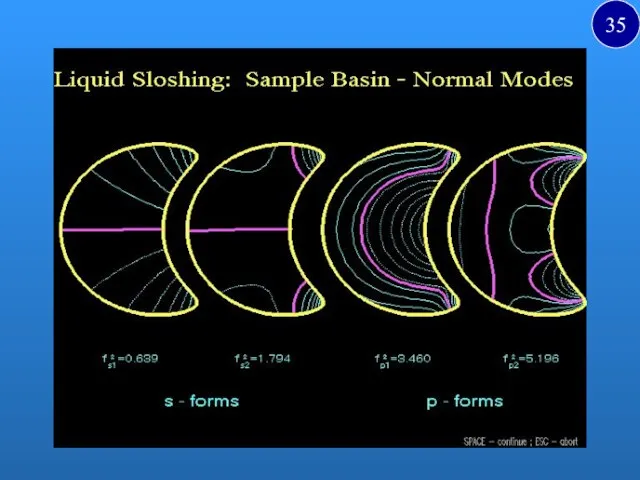
- 30. Chapter 5 Liquid Sloshing in Cavities Boundary-value problems of fluid dynamics in cavities and equations of
- 31. 31
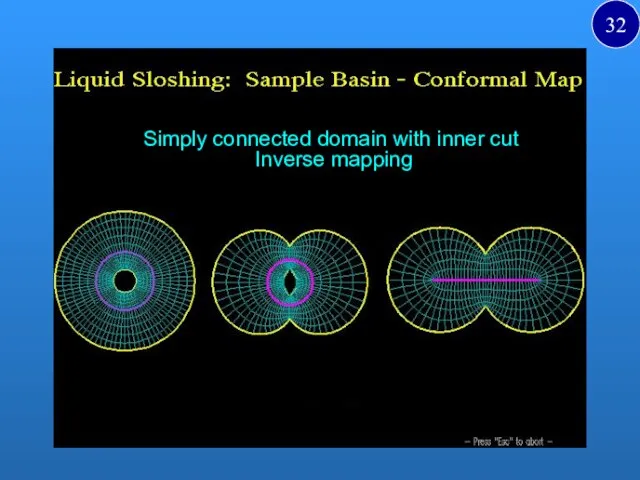
- 32. Simply connected domain with inner cut Inverse mapping i 32
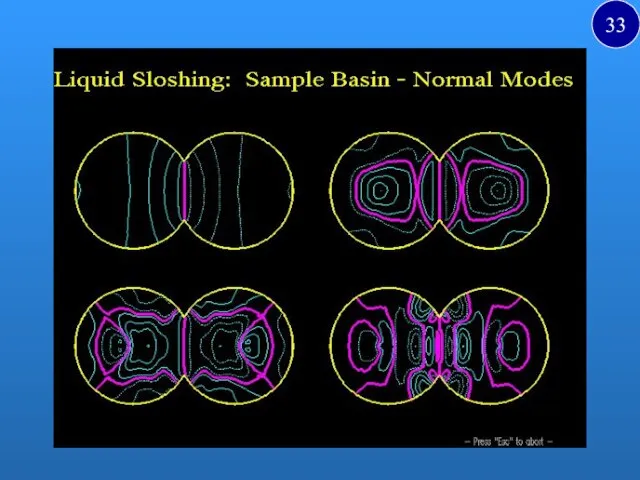
- 33. 33
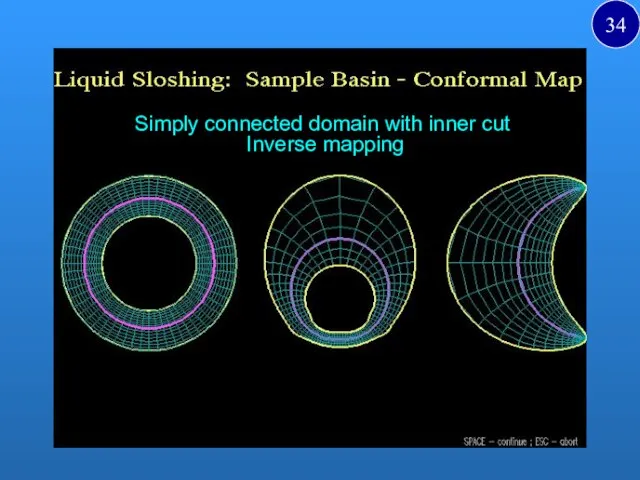
- 34. Simply connected domain with inner cut Inverse mapping i 34
- 35. 35
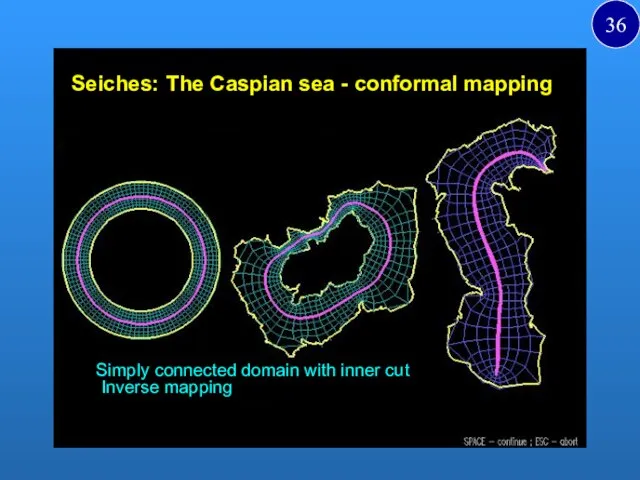
- 36. Seiches: The Caspian sea - conformal mapping Simply connected domain with inner cut Inverse mapping i
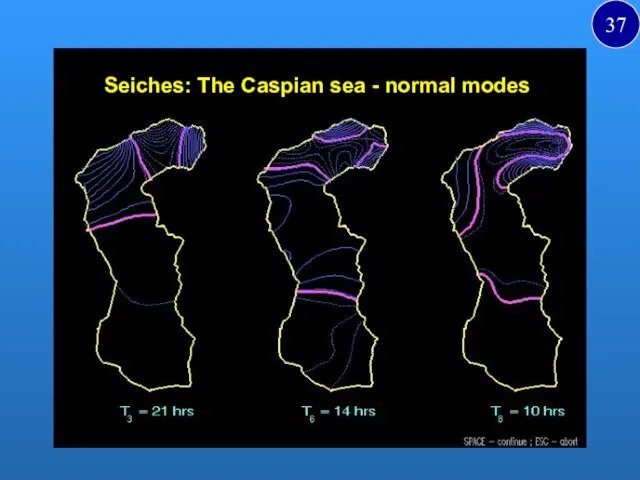
- 37. Seiches: The Caspian sea - normal modes 37
- 38. Conclusions The Notation Table 1 The methods used for solution of the boundary-value problems 38
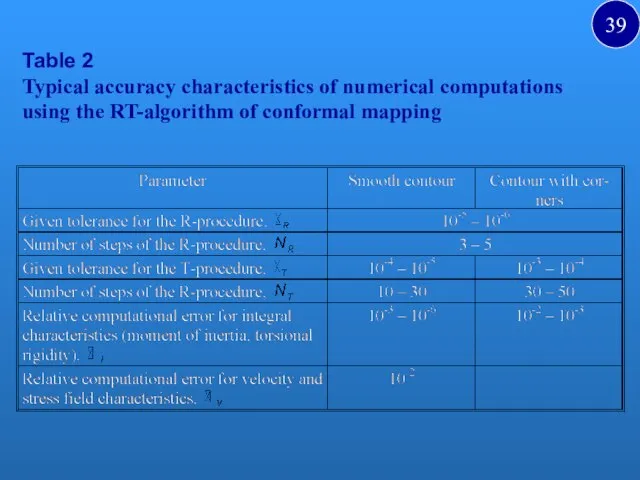
- 39. Table 2 Typical accuracy characteristics of numerical computations using the RT-algorithm of conformal mapping 39
- 40. NUMERICAL METHODS IN FLUID MECHANICS SPACE RESEARCH INSTITUTE RUSSIAN ACADEMY OF SCIENCES
- 42. Скачать презентацию















 Европейский рынок лизинга и перспективы развития лизинга в России
Европейский рынок лизинга и перспективы развития лизинга в России Аник Автоматизация. Эффективная работа
Аник Автоматизация. Эффективная работа Танцевальная группа Русские узоры в Международном фестивале Вуокса - река дружбы
Танцевальная группа Русские узоры в Международном фестивале Вуокса - река дружбы Verbi irregolari. Lezione 6-2
Verbi irregolari. Lezione 6-2 Великий круговорот жизни 3 класс
Великий круговорот жизни 3 класс Простое прошедшее время в английском
Простое прошедшее время в английском Devohki,vnimanie
Devohki,vnimanie Межличностные отношения в классном коллективе
Межличностные отношения в классном коллективе Национализм как политическая идеология
Национализм как политическая идеология Последовательное и параллельное соединения проводников
Последовательное и параллельное соединения проводников Проект Красная книга Бабочка -махаон
Проект Красная книга Бабочка -махаон Звери
Звери mon_cours_nouveau-ne_volet__2_copie_etud
mon_cours_nouveau-ne_volet__2_copie_etud Фосфор
Фосфор МОУ «СОШ № 56 г. Орск»Родительский всеобуч
МОУ «СОШ № 56 г. Орск»Родительский всеобуч Физическая сила. Виды силы
Физическая сила. Виды силы Радиоактивные превращения атомных ядер. Правила смещения
Радиоактивные превращения атомных ядер. Правила смещения Футбол. Тренажёр по английскому языку
Футбол. Тренажёр по английскому языку Презентация на тему Макраме
Презентация на тему Макраме Основная образовательная программаначального общего образования
Основная образовательная программаначального общего образования Компания объединенных кредитных карточек
Компания объединенных кредитных карточек Славный город мой Асбест
Славный город мой Асбест Sahul. Catalog
Sahul. Catalog От опорных конспектов – к алгоритмизации и компьютеризации
От опорных конспектов – к алгоритмизации и компьютеризации Психология деятельности специалиста по социальной работе по профилактике девиантного поведения подростков на основе анализа
Психология деятельности специалиста по социальной работе по профилактике девиантного поведения подростков на основе анализа Present Simple
Present Simple Классификация видов групп однородной продукции и их характеристики
Классификация видов групп однородной продукции и их характеристики Привет В зоопарке
Привет В зоопарке