ДЕКАРТОВА СИСТЕМА КООРДИНАТ

Рене Декарт (1596-1650 гг.)
Декарт (Descartes) Рене ‑ французский философ, математик, физик и физиолог.
Рене Декарт является одним из создателей аналитической геометрии (которую он разрабатывал одновременно с П. Ферма), позволявшей алгебраизировать эту науку с помощью метода координат, т.е. вместо геометрических построений использовать математические расчеты. Предложенная им система координат получила его имя.

Декартова система координат

Однажды Рене Декарт весь день пролежал в кровати, думая о чем-то, а муха жужжала вокруг и не давала ему сосредоточиться. Он стал размышлять, как бы описать положение мухи в любой момент времени математически, чтобы иметь возможность прихлопнуть ее без промаха.
И ... придумал декартовы координаты, одно из величайших изобретений в истории человечества.
ЛЕГЕНДА ОБ ИЗОБРЕТЕНИИ
СИСТЕМЫ КООРДИНАТ

Проследим путь открытия системы координат согласно этой легенде.
Время открытия: 1637 год.
Действующие лица:
1)Автор открытия: французский математик Рене Декарт.
2)"Соавтор" открытия: муха Декарта
Место действия: "кабинет" Рене Декарта.

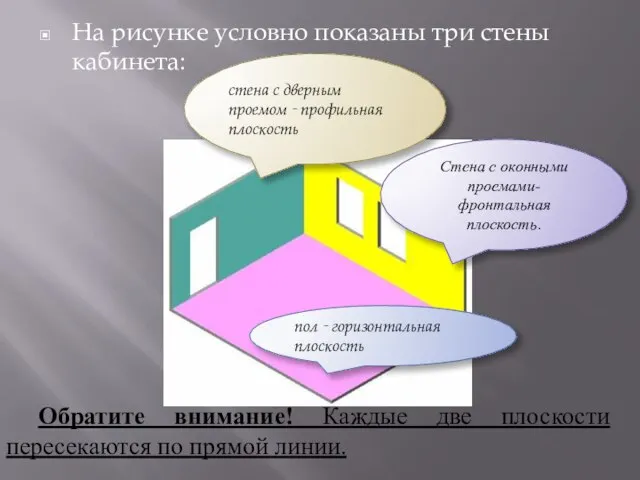
На рисунке условно показаны три стены кабинета:
Обратите внимание! Каждые две плоскости пересекаются по прямой линии.
стена с дверным проемом ‑ профильная плоскость
Стена с оконными проемами- фронтальная плоскость.
пол ‑ горизонтальная плоскость

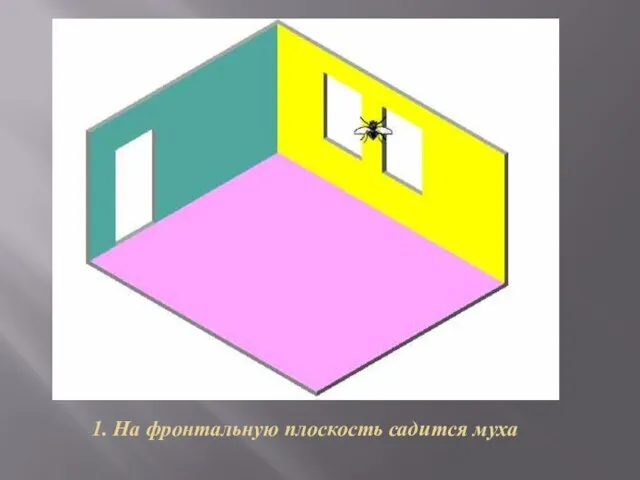
1. На фронтальную плоскость садится муха

2. Предположим, что Р. Декарт смотрит на фронтальную плоскость в перпендикулярном ей направлении.

Мы видим, что муха находится на фронтальной плоскости.
Но как точно определить ее положение?

3) Эврика! НУЖНО взять две взаимно перпендикулярные числовые прямые.
Точку пересечения прямых обозначим как О ‑ начало системы координат.
Одну из прямых назовем ось X, другую ‑ ось Y.
На нашем рисунке расстояние между делениями на числовых прямых равно единице.

4. Определим точное положение "соавтора" ‑ мухи.
Проведем через точку, где находится муха две прямые:
А) Параллельно оси X. Прямая пересекает ось Y в точке с числовым значением, равным 4. Это значение назовем координатой "у" нашего "соавтора".
Б) Параллельно оси Y. Прямая пересекает ось Х в точке с числовым значением, равным (-2). Это значение назовем координатой "х" нашего объекта.

Принято координаты объекта, обычно точки, записывать в форме (x; y).
Для нашей мухи мы можем сказать, что она находится в точке с координатами (-2; 4).
Задача точного определения положения мухи решена!

Новизна идеи состоит в том, что положение точки или объекта на плоскости определяетcя с помощью двух пересекающихся осей.

Точно так же можно поступить и для определения положения мухи на потолке.

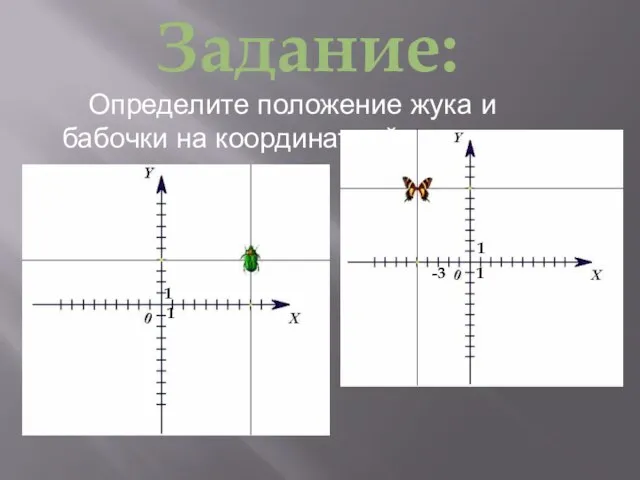
Определите положение жука и бабочки на координатной плоскости.
Задание:
1
1
-3 1
1