Содержание
- 2. Упражнение 1 Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного
- 3. Упражнение 2 Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол. Верно ли утверждение о
- 4. Упражнение 3 Треугольник MAB и квадрат ABCD заданы таким образом, что MB - перпендикуляр к плоскости
- 5. Упражнение 4 В правильной треугольной призме найдите угол между боковыми гранями. Ответ: 60о.
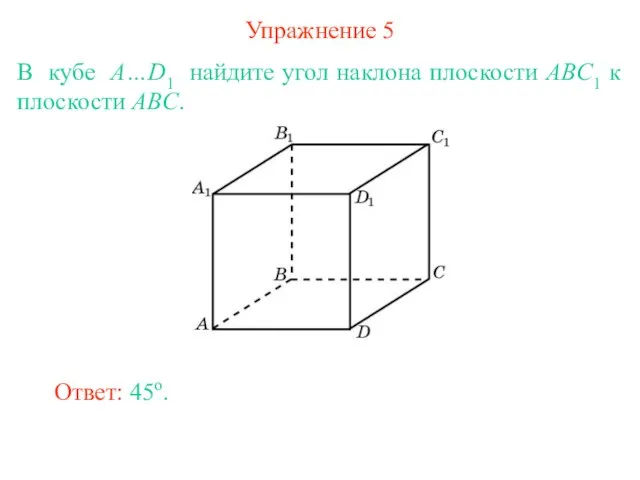
- 6. Упражнение 5 В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC. Ответ: 45о.
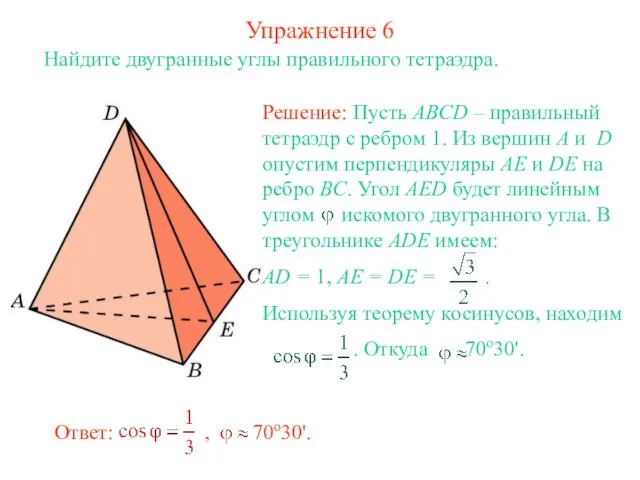
- 7. Упражнение 6 Найдите двугранные углы правильного тетраэдра.
- 8. Упражнение 7 Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся плоскостей. Ответ: Две биссектральные
- 9. Упражнение 8 Через сторону BC треугольника ABC проведена плоскость α под углом 30° к плоскости треугольника.
- 10. Упражнение 9 Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен 90°) проведена плоскость α,
- 11. Упражнение 10 Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника; угол
- 12. Упражнение 11 Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена плоскость α, образующая с
- 13. Упражнение 12 Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды. Верно ли, что двугранные
- 14. Упражнение 13 В основании прямой призмы параллелограмм со сторонами 4 дм и 5 дм. Угол между
- 15. Упражнение 14 Боковое ребро прямой призмы равно 6 см. Ее основание – прямоугольный треугольник с катетами
- 16. Упражнение 15 Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь сечения призмы плоскостью, проходящей
- 17. Упражнение 16 Ребро куба равно a. Найдите площадь сечения куба плоскостью, проходящей через сторону основания, если
- 18. Упражнение 17 Через середины двух смежных сторон основания правильной четырехугольной призмы проведена плоскость, образующая с плоскостью
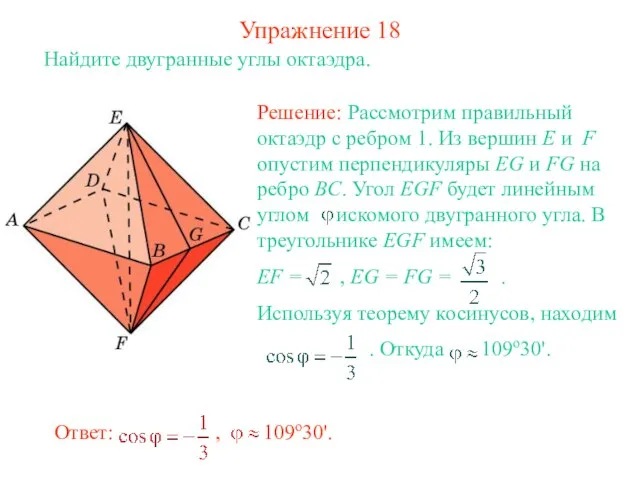
- 19. Упражнение 18 Найдите двугранные углы октаэдра.
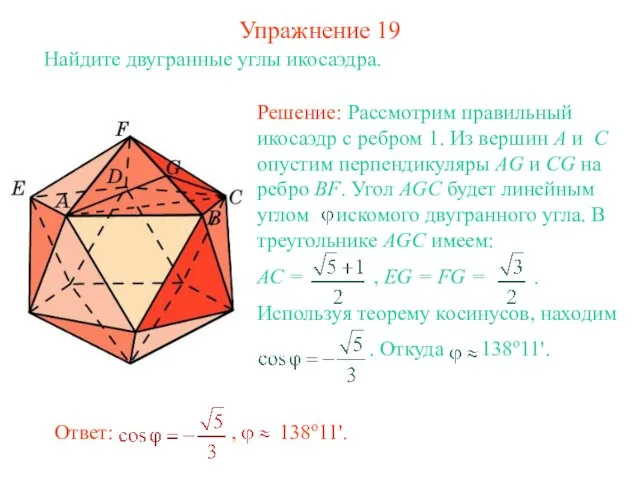
- 20. Упражнение 19 Найдите двугранные углы икосаэдра.
- 22. Скачать презентацию















 18-19. Сочинение по картине. Развитие речи
18-19. Сочинение по картине. Развитие речи Презентация на тему Заглавная буква (1 класс)
Презентация на тему Заглавная буква (1 класс) Долгосрочная Интегрированная Программа Деловых Партнерств«Россия – Европа: Сотрудничество безГраниц» МОО МАП
Долгосрочная Интегрированная Программа Деловых Партнерств«Россия – Европа: Сотрудничество безГраниц» МОО МАП Эффективное использование современных инновационных технологий на уроках в начальной школе Учитель МОУ Борской СОШ №1 «ОЦ» Га
Эффективное использование современных инновационных технологий на уроках в начальной школе Учитель МОУ Борской СОШ №1 «ОЦ» Га Как помочь ребенку стать внимательным?
Как помочь ребенку стать внимательным? Русский лес
Русский лес презентация урок тигра (1) (2)
презентация урок тигра (1) (2) ТЕМА 6 «АДАПТАЦИЯ ПЕРСОНАЛА»
ТЕМА 6 «АДАПТАЦИЯ ПЕРСОНАЛА»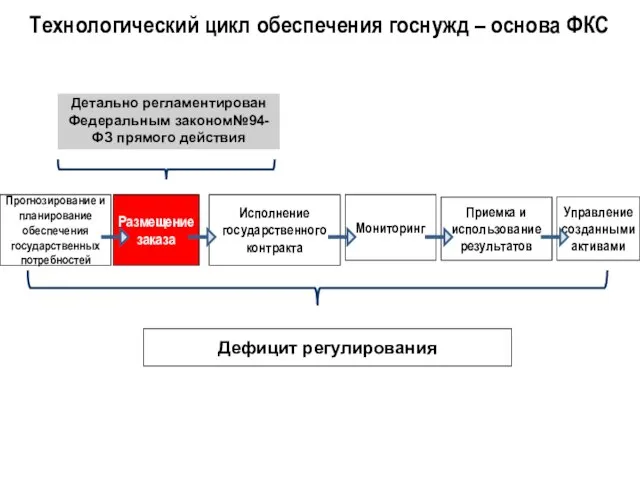 Технологический цикл обеспечения госнужд – основа ФКС
Технологический цикл обеспечения госнужд – основа ФКС Классификация объектов складской недвижимости по отношению к базисным функциональным областям логистики
Классификация объектов складской недвижимости по отношению к базисным функциональным областям логистики «Вегетативное размножение махровой глоксинии листовыми черенками»
«Вегетативное размножение махровой глоксинии листовыми черенками» Методический материал по профилактике наркомании
Методический материал по профилактике наркомании ГОУ школа №637 Московского района Санкт-Петербурга
ГОУ школа №637 Московского района Санкт-Петербурга Электромагнит, электронное реле и герконы
Электромагнит, электронное реле и герконы Львиные ворота
Львиные ворота  Либертарианское самбо Вадим Новиков
Либертарианское самбо Вадим Новиков «Проект по предмету «Изобразительное искусство» для учащихся 3 класса « Виды росписи»
«Проект по предмету «Изобразительное искусство» для учащихся 3 класса « Виды росписи» Научно-практическая конференция по математике Банковские кредиты. Мухаметшина Элина 5М 2013 год
Научно-практическая конференция по математике Банковские кредиты. Мухаметшина Элина 5М 2013 год Моя осень в кадрах
Моя осень в кадрах Былина как вид фольклора
Былина как вид фольклора Предлог
Предлог Что такое биржа
Что такое биржа
 Учет фактора риска
Учет фактора риска Повышение роли первичного звена здравоохранения в профилактике ВИЧ/СПИД/ИППП среди подростков и молодых людей группы высокого ри
Повышение роли первичного звена здравоохранения в профилактике ВИЧ/СПИД/ИППП среди подростков и молодых людей группы высокого ри Внешняя политика Николая I 1826-1849 гг
Внешняя политика Николая I 1826-1849 гг кп к уроку 3
кп к уроку 3 Стилистическая карта клиента
Стилистическая карта клиента Лозоплетение — ремесло изготовления плетёных изделий из лозы
Лозоплетение — ремесло изготовления плетёных изделий из лозы