Электрические цепи однофазного синусоидального тока. Общие сведения

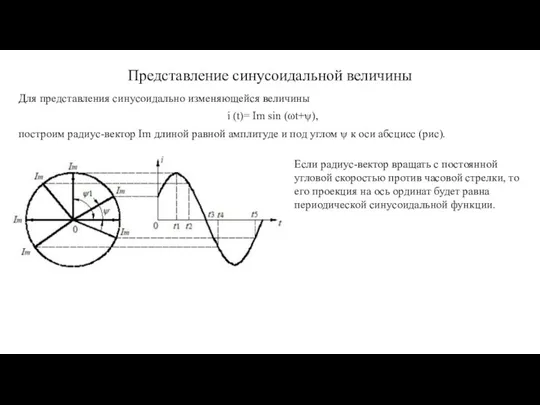
Представление синусоидальной величины
Для представления синусоидально изменяющейся величины
i (t)= Im sin (ωt+ψ),
построим радиус-вектор Im длиной равной амплитуде и под углом ψ к оси абсцисс (рис).
Если радиус-вектор вращать с постоянной угловой скоростью против часовой стрелки, то его проекция на ось ординат будет равна периодической синусоидальной функции.

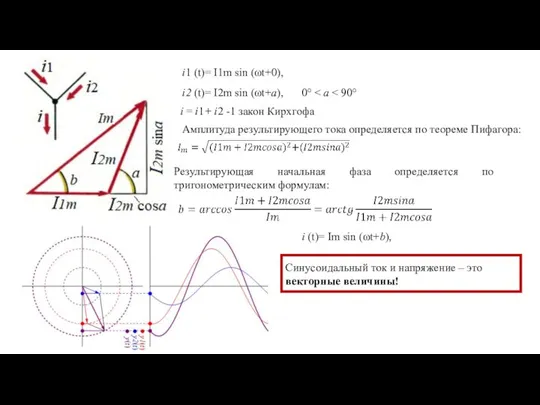
i1 (t)= I1m sin (ωt+0),
i2 (t)= I2m sin (ωt+а),
Амплитуда результирующего тока определяется по теореме Пифагора:
i = i1+ i2 -1 закон Кирхгофа
0° < а < 90°
Результирующая начальная фаза определяется по тригонометрическим формулам:
i (t)= Im sin (ωt+b),
Синусоидальный ток и напряжение – это векторные величины!

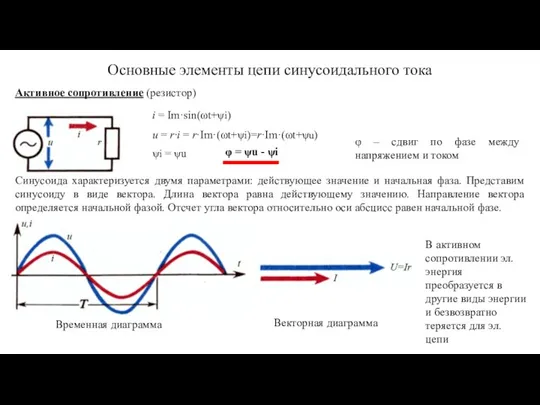
Векторная диаграмма
Основные элементы цепи синусоидального тока
Активное сопротивление (резистор)
i = Im·sin(ωt+ψi)
u = r·i = r·Im·(ωt+ψi)=r·Im·(ωt+ψu)
ψi = ψu
Временная диаграмма
Синусоида характеризуется двумя параметрами: действующее значение и начальная фаза. Представим синусоиду в виде вектора. Длина вектора равна действующему значению. Направление вектора определяется начальной фазой. Отсчет угла вектора относительно оси абсцисс равен начальной фазе.
φ = ψu - ψi
φ – сдвиг по фазе между напряжением и током
В активном сопротивлении эл. энергия преобразуется в другие виды энергии и безвозвратно теряется для эл. цепи

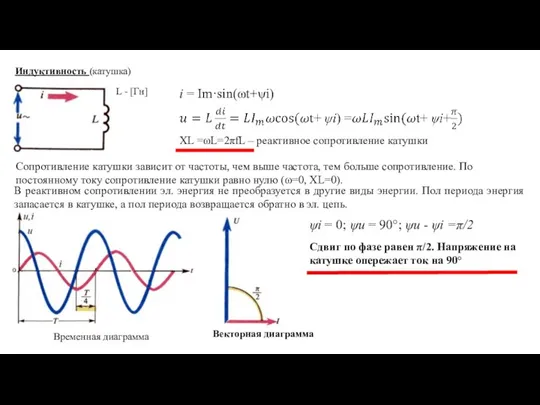
Векторная диаграмма
Индуктивность (катушка)
i = Im·sin(ωt+ψi)
Временная диаграмма
В реактивном сопротивлении эл. энергия не преобразуется в другие виды энергии. Пол периода энергия запасается в катушке, а пол периода возвращается обратно в эл. цепь.
L - [Гн]
XL =ωL=2πfL – реактивное сопротивление катушки
Сопротивление катушки зависит от частоты, чем выше частота, тем больше сопротивление. По постоянному току сопротивление катушки равно нулю (ω=0, XL=0).
ψi = 0; ψu = 90°; ψu - ψi =π/2
Сдвиг по фазе равен π/2. Напряжение на катушке опережает ток на 90°

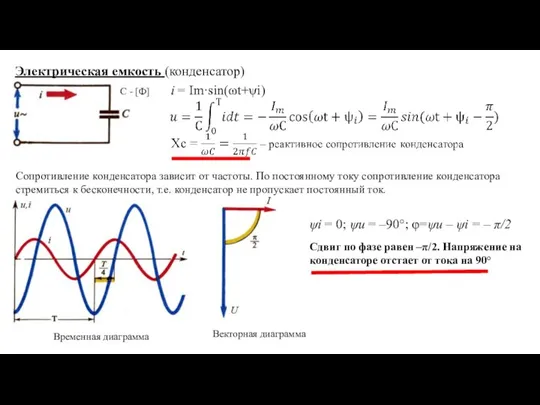
Векторная диаграмма
Электрическая емкость (конденсатор)
i = Im·sin(ωt+ψi)
Временная диаграмма
С - [Ф]
Сопротивление конденсатора зависит от частоты. По постоянному току сопротивление конденсатора стремиться к бесконечности, т.е. конденсатор не пропускает постоянный ток.
ψi = 0; ψu = –90°; φ=ψu – ψi = – π/2
Сдвиг по фазе равен –π/2. Напряжение на конденсаторе отстает от тока на 90°

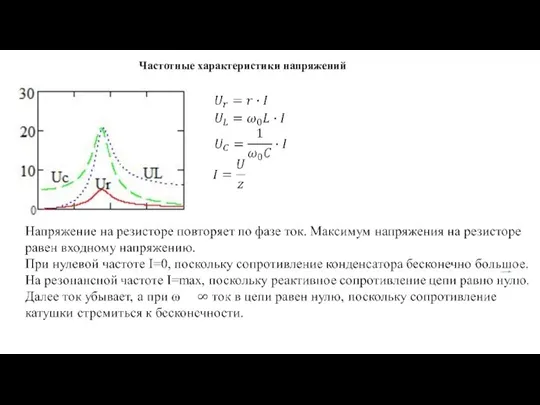
Таким образом, в цепях синусоидального тока напряжение и токи элементов характеризуются не только величиной, но и начальной фазой. Это векторные величины, их нельзя складывать скалярно как в цепях постоянного тока.
Метод векторных диаграмм
Нельзя алгебраически складывать сопротивления элементов, т.к. они имеют разные фазы !!!
При последовательном соединении построение векторной диаграммы начинают с вектора тока. Вектор тока откладывают произвольной длины и под любым углом, равным начальной фазе (для наглядности и простоты построения принята начальная фаза тока равной нулю).
Задача:

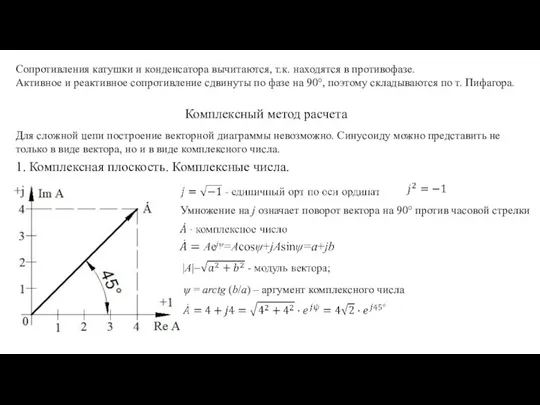
Сопротивления катушки и конденсатора вычитаются, т.к. находятся в противофазе.
Активное и реактивное сопротивление сдвинуты по фазе на 90°, поэтому складываются по т. Пифагора.
Комплексный метод расчета
Для сложной цепи построение векторной диаграммы невозможно. Синусоиду можно представить не только в виде вектора, но и в виде комплексного числа.
1. Комплексная плоскость. Комплексные числа.
Умножение на j означает поворот вектора на 90° против часовой стрелки
ψ = arctg (b/a) – аргумент комплексного числа

Заменим синусоидальное напряжение и токи на комплексные числа
2. Комплексное сопротивление резистора, катушки и конденсатора
φ=ψu - ψi =π/2

φ=ψu – ψi = – π/2
3. Представление синусоиды в комплексное число
e(t) = Em·sin(ωt+ψ)
Модуль
Модуль комплексного числа равен действующему значению!
e(t) = 141·sin(ωt – 45°)

4.Последовательность использования комплексного метода
Переходим к комплексной схеме замещения;
Проводим расчет эл цепи, которая включает одни резисторы с комплексными значениями;
Результат расчета – комплексные токи и напряжения записываются в показательной форме, тогда модуль комплексного числа равен действующему значению тока и напряжения, а аргумент комплексного числа равен начальной фазе.
В цепи течет комплексный ток, который нужно найти
Перейдём к показательной форме записи тока

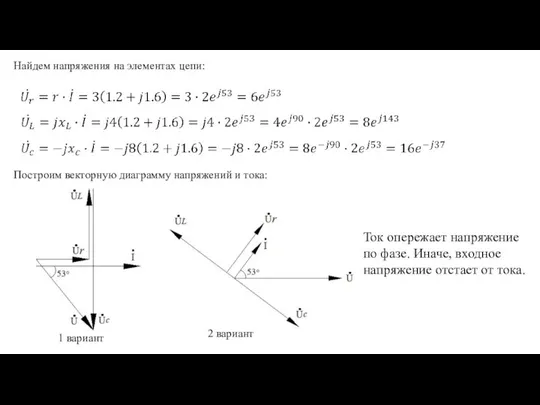
Найдем напряжения на элементах цепи:
Построим векторную диаграмму напряжений и тока:
1 вариант
2 вариант
Ток опережает напряжение по фазе. Иначе, входное напряжение отстает от тока.

Комплексное сопротивление и комплексная проводимость
-90° - C
(-90° ,0) – RC
0 – R
(0, 90°) – RL
90° - L
φ=
Комплексная проводимость – величина, обратная комплексному сопротивлению
g – активная проводимость
b – реактивная проводимость
Треугольник сопротивлений
Треугольник проводимостей

Мощность в цепях синусоидального тока
Треугольник мощностей
– сдвиг по фазе между U и I
-активная мощность, [Вт]
Активная мощность – это полезная мощность, она преобразуется в другие виды энергии. Она выделяется в резисторах или в активных сопротивлениях
-реактивная мощность, [Вар или вар]
Реактивная мощность – полезной работы не совершает. Пол периода она запасается в реактивных элементах (катушке и конденсаторе) и пол периода возвращается обратно в цепь.
-полная мощность, [ВА]

Резонанс в электрических цепях
Сопротивление катушки и конденсатора зависит от частоты, с увеличением частоты сопротивление катушки возрастает, сопротивление конденсатора уменьшается, следовательно при последовательном соединении катушки и конденсатора возможна ситуация, когда реактивное сопротивление цепи равно нулю – режим резонанса.
XL =ωL

Резонанс в электрических цепях
Найдем напряжение на реактивных элементах:
В режиме резонанса напряжения на катушке и конденсаторе равны!
Добротность – это кратность превышения напряжения на реактивных элементах к входному напряжению.
Пусть ωL>>r, что имеет место на высоких частотах, то Q>>1.
Из-за возможности скачка напряжения на реактивных элементах данный вид резонанса называется резонансом напряжений.

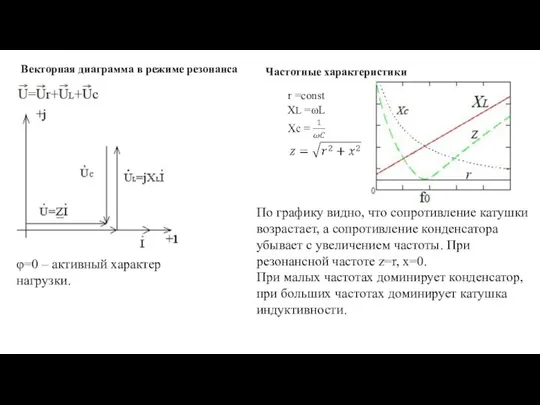
Векторная диаграмма в режиме резонанса
φ=0 – активный характер нагрузки.
Частотные характеристики
XL =ωL
r =const
По графику видно, что сопротивление катушки возрастает, а сопротивление конденсатора убывает с увеличением частоты. При резонансной частоте z=r, х=0.
При малых частотах доминирует конденсатор, при больших частотах доминирует катушка индуктивности.

Частотные характеристики напряжений

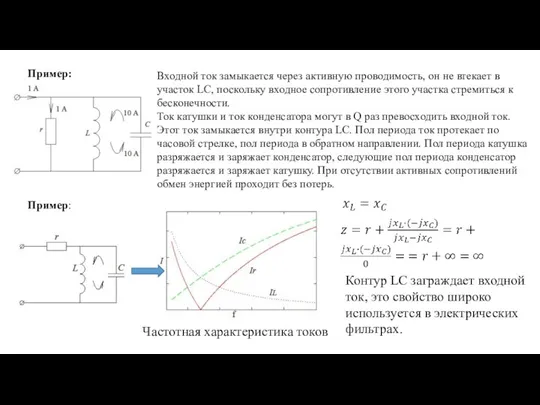
Резонанс в параллельной ветви или резонанс токов
В режиме резонанса входная проводимость минимальна или входное сопротивление максимально.
Добротность показывает во сколько раз ток реактивных элементов превышает ток в режиме резонанса.

Входной ток замыкается через активную проводимость, он не втекает в участок LC, поскольку входное сопротивление этого участка стремиться к бесконечности.
Ток катушки и ток конденсатора могут в Q раз превосходить входной ток. Этот ток замыкается внутри контура LC. Пол периода ток протекает по часовой стрелке, пол периода в обратном направлении. Пол периода катушка разряжается и заряжает конденсатор, следующие пол периода конденсатор разряжается и заряжает катушку. При отсутствии активных сопротивлений обмен энергией проходит без потерь.
Пример:
Пример:
Частотная характеристика токов
Контур LC заграждает входной ток, это свойство широко используется в электрических фильтрах.

Расчет цепей с взаимной индукцией
В состав электрических цепей могут входить катушки, магнитно связанные с другими катушками. Поток одной из них пронизывает другие и наводит в них ЭДС взаимоиндукции, которые необходимо учесть при расчете. При составлении уравнений для магнитносвязанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции.
Направление потоков самоиндукции и взаимоиндукции двух катушек с током
Для определения направления магнитного потока используют правило правой руки

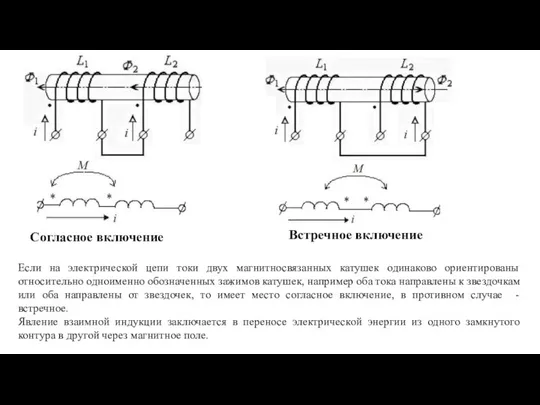
Согласное включение
Встречное включение
Если на электрической цепи токи двух магнитносвязанных катушек одинаково ориентированы относительно одноименно обозначенных зажимов катушек, например оба тока направлены к звездочкам или оба направлены от звездочек, то имеет место согласное включение, в противном случае - встречное.
Явление взаимной индукции заключается в переносе электрической энергии из одного замкнутого контура в другой через магнитное поле.

Индуктивность увеличилась, это связано с тем, что на поток самоиндукции накладывается поток взаимной индукции из второй катушки. Поскольку индуктивность цепи увеличилась, а значит уменьшился ток в цепи по сравнению с той же цепью, но без взаимной индуктивности катушек.
Согласное включение катушек
Перед слагаемым jωM стоит тот же знак, что и перед jωL, т.к. ток входит в одноименные зажимы катушек, т.е. имеем согласное включение

Индуктивность снизилась, а значит увеличится ток в цепи по сравнению с той же цепью, но без взаимной индуктивности катушек. Взаимная индуктивность при встречном включении подобна емкости. Ток при встречном включении всегда выше, чем при согласном. Встречное включение узнаем по большему току.
Встречное включение катушек
Перед слагаемым jωM стоит знак минус, т.к. ток входит в разноименные зажимы катушек, т.е. имеем встречное включение

к=0 – магнитная связь отсутствует
к=1 – идеальная магнитная связь
При идеальной магнитной связи весь магнитный поток, создаваемый первой катушкой замыкается через вторую катушку и наоборот. Поток рассеивания отсутствует.
Задача: Определить как изменится ток в цепи с двумя катушками, обладающие магнитной связью, если их переключить с согласного включения на встречное.
Пусть L1=L2
коэффициент магнитной связи между одинаковыми катушками
коэффициент магнитной связи между разными катушками

Ток увеличился в 3 раза
Пусть к = 0.5 – слабая магнитная связь (половина магнитного потока не долетает до второй катушки. Такая магнитная связь присуща катушкам без сердечника)
Пусть к = 0.9 – средняя магнитная связь (маломощны трансформатор с сердечником)
Бросок тока в 19 раз
Пусть к = 0.99 – сильная магнитная связь
Бросок тока в 199 раз
В электроэнергетике включение катушек всегда согласное.
В системах автоматики и связи, наоборот, стремятся к встречному включению.
При встречном включении индуктивность соединительных элементов минимально, поэтому и их сопротивление минимально.
т.о. для катушек, обладающих магнитной связью, способ соединения обмоток имеет решающее значение, нельзя путать согласное и встречное включение.

Задача: Две катушки, одна мощная, другая – маломощная, включены встречно, определить условия работы второй катушки.
L1>>L2; M>L2
Комплексное сопротивление второй катушки отрицательно, точно так же как у конденсатора. По электрическим свойствам из индуктивности получили емкость.