Содержание
- 2. К числу прямых, занимающих особое положение в плоскости, относятся линии уровня и линии наибольшего наклона плоскости
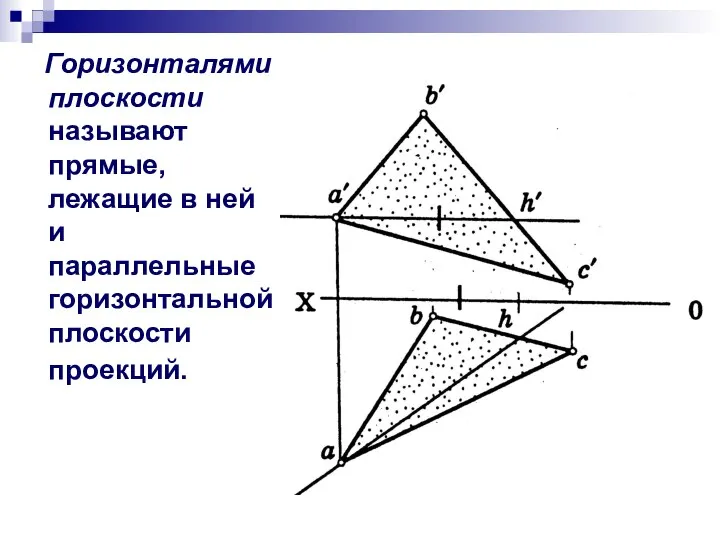
- 3. Горизонталями плоскости называют прямые, лежащие в ней и параллельные горизонтальной плоскости проекций.
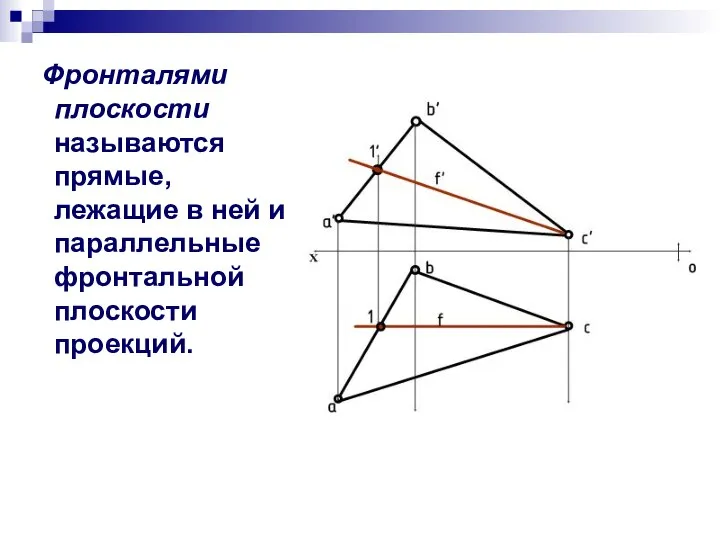
- 4. Фронталями плоскости называются прямые, лежащие в ней и параллельные фронтальной плоскости проекций.
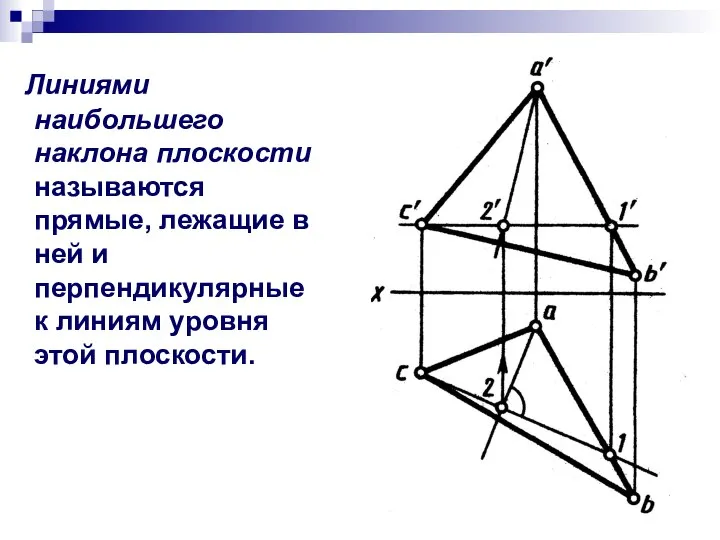
- 5. Линиями наибольшего наклона плоскости называются прямые, лежащие в ней и перпендикулярные к линиям уровня этой плоскости.
- 6. Линия наибольшего наклона плоскости позволяет определить углы наклона заданной плоскости к плоскостям проекций.
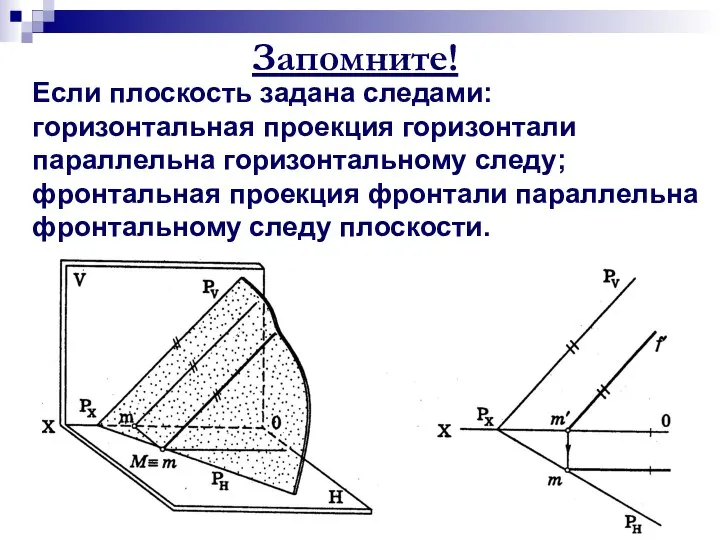
- 7. Запомните! Если плоскость задана следами: горизонтальная проекция горизонтали параллельна горизонтальному следу; фронтальная проекция фронтали параллельна фронтальному
- 8. *1. В плоскости общего положения провести фронталь на расстоянии 25 мм от плоскости и взять на
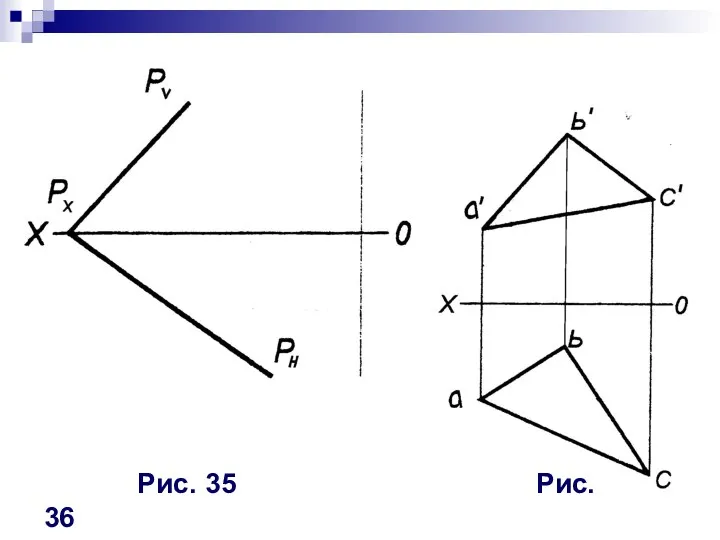
- 9. Рис. 35 Рис. 36
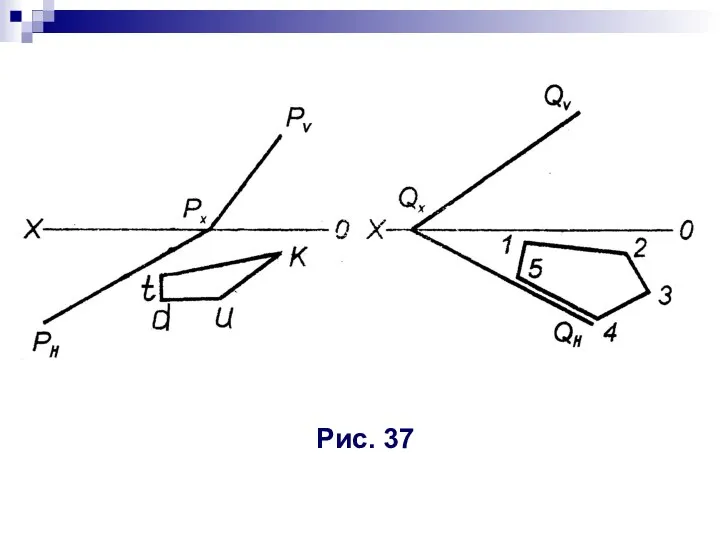
- 10. Рис. 37
- 11. Параллельность прямой и плоскости. Параллельность двух плоскостей
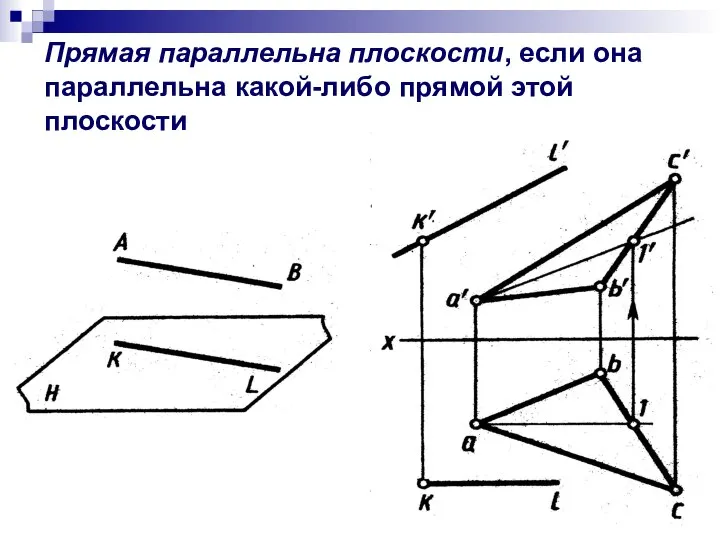
- 12. Прямая параллельна плоскости, если она параллельна какой-либо прямой этой плоскости
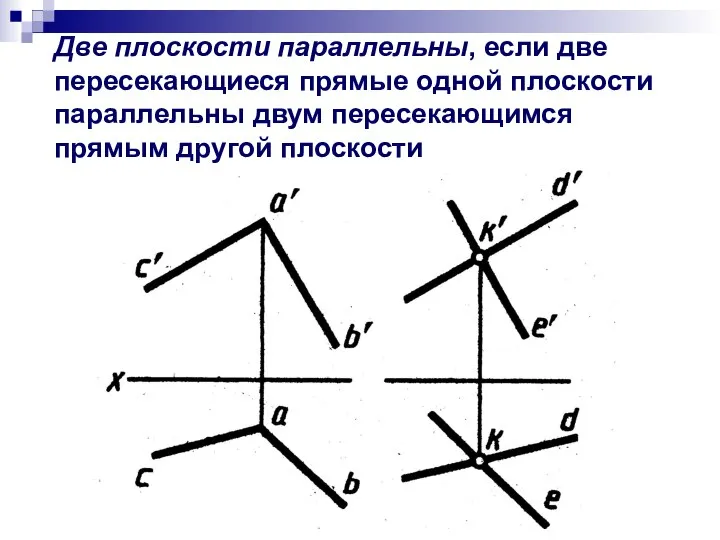
- 13. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости
- 14. Перпендикулярность прямой и плоскости Прямой угол, образованный двумя пересекающимися прямыми линиями, в зависимости от расположения его
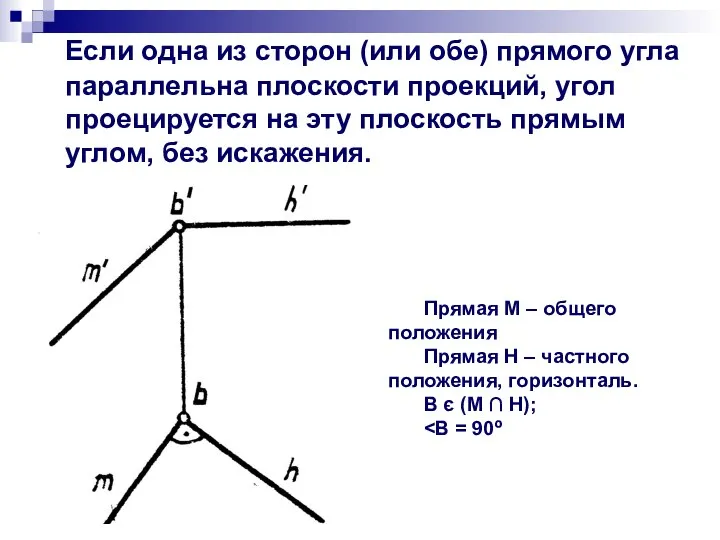
- 15. Если одна из сторон (или обе) прямого угла параллельна плоскости проекций, угол проецируется на эту плоскость
- 16. Перпендикулярность прямой и плоскости Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Практически
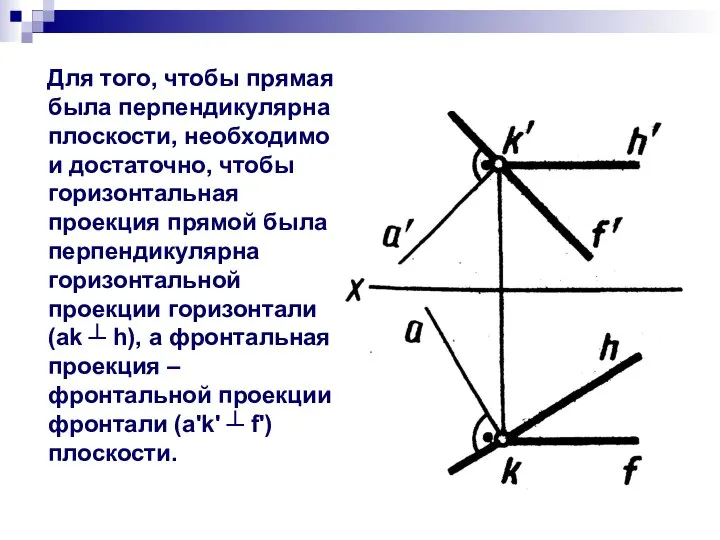
- 17. Для того, чтобы прямая была перпендикулярна плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была перпендикулярна
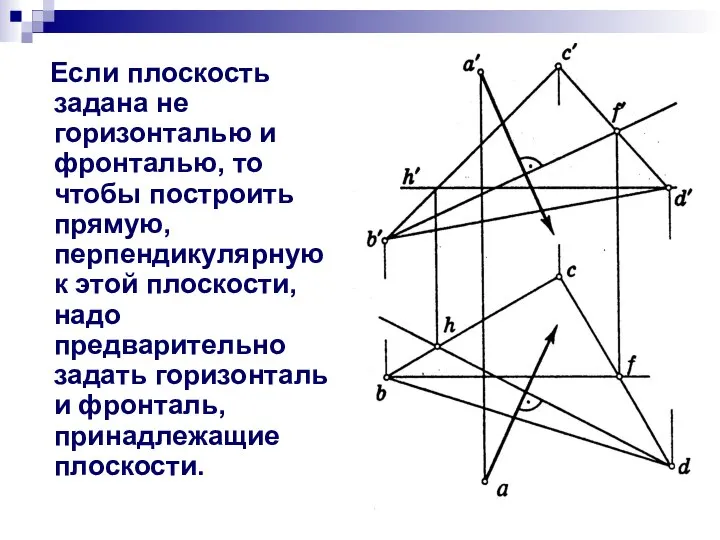
- 18. Если плоскость задана не горизонталью и фронталью, то чтобы построить прямую, перпендикулярную к этой плоскости, надо
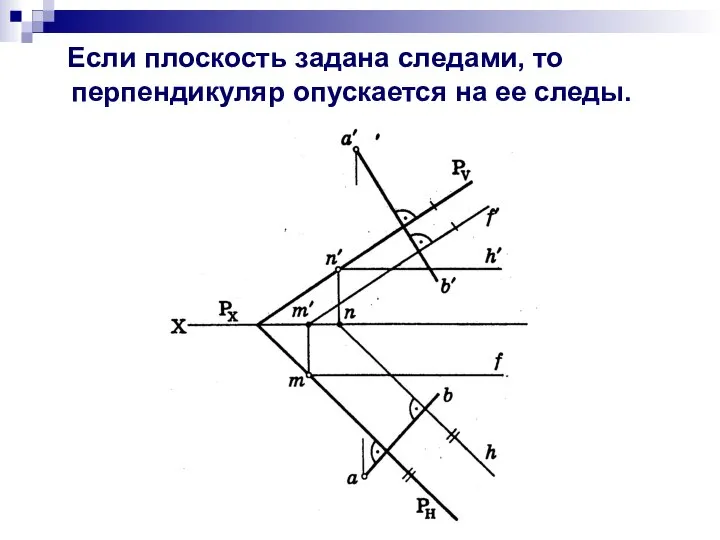
- 19. Если плоскость задана следами, то перпендикуляр опускается на ее следы.
- 21. Скачать презентацию






 Модель компетенций и знаний выпускника по направлению Гидрогеология
Модель компетенций и знаний выпускника по направлению Гидрогеология Презентация на тему Г. Х. Андерсен. Жизнь и творчество
Презентация на тему Г. Х. Андерсен. Жизнь и творчество Расторжение трудового договора по инициативе работодателя
Расторжение трудового договора по инициативе работодателя Урок 1. Давайте познакомимся
Урок 1. Давайте познакомимся Минимализм
Минимализм Виды ответственности за нарушение авторских прав
Виды ответственности за нарушение авторских прав  ПРОБЛЕМА 01.01.10
ПРОБЛЕМА 01.01.10 Род деятельности. Я осознанно выбираю профессию
Род деятельности. Я осознанно выбираю профессию Порядок осмотра, способы проверки автосцепного устройства. Требования ПТЭ и инструкций к автосцепным устройствам электропоездов
Порядок осмотра, способы проверки автосцепного устройства. Требования ПТЭ и инструкций к автосцепным устройствам электропоездов Презентация на тему О – Ё после шипящих в корнях слов
Презентация на тему О – Ё после шипящих в корнях слов 1- Промышленность 2-Сельское и лесное хозяйство 3-Строительство 4-Транспорт и связь 5-Торговля, общепит 6-ЖКХ 7-бытовое обслуживание 8-З
1- Промышленность 2-Сельское и лесное хозяйство 3-Строительство 4-Транспорт и связь 5-Торговля, общепит 6-ЖКХ 7-бытовое обслуживание 8-З Системы управления и диспетчеризации инженерной инфраструктуры ЦОД
Системы управления и диспетчеризации инженерной инфраструктуры ЦОД ERPII от 1С как путь к успешному профессиональному развитию
ERPII от 1С как путь к успешному профессиональному развитию Особенности контрактов на комплектное оборудование Гудимова К. С., Мельник Д.А. гр. МЭ091
Особенности контрактов на комплектное оборудование Гудимова К. С., Мельник Д.А. гр. МЭ091 Оригами
Оригами Праздник «ЗОЛОТАЯ ОСЕНЬ»
Праздник «ЗОЛОТАЯ ОСЕНЬ» Компьютер и здоровье 10 класс
Компьютер и здоровье 10 класс Ускоренные производства в гражданском процессе
Ускоренные производства в гражданском процессе Вооружение Российской Армии
Вооружение Российской Армии Пространство, размерность
Пространство, размерность инструменты в гараже
инструменты в гараже Организация работы с дошкольниками по ручному труду
Организация работы с дошкольниками по ручному труду Урок 3
Урок 3 Сила трения покоя
Сила трения покоя Презентація послуги Інтереактивне ТВ
Презентація послуги Інтереактивне ТВ през пр деят
през пр деят Государство, его признаки и формы
Государство, его признаки и формы «Институциональные блокировки в трансформационных экономиках и возможности их преодоления» Аузан Александр Александрович
«Институциональные блокировки в трансформационных экономиках и возможности их преодоления» Аузан Александр Александрович