Электростатика

Тема 5. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
5.1. Напряженность и потенциал электростатического поля в проводнике.
5.2. Определение напряженности электростатического поля вблизи проводника.
5.3. Экспериментальная проверка распределения заряда на проводнике.
5.4. Конденсаторы.
5.4.1. Электрическая емкость. Конденсаторы.
5.4.2. Соединение конденсаторов.
5.4.3. Расчет емкостей различных конденсаторов.
5.4.4. Энергия заряженного конденсатора.
5.5. Энергия электростатического поля.

В проводниках имеются электрически заряженные частицы – носители заряда (электроны в металлах, ионы в электролитах), способные перемещаться по всему объему проводника под действием внешнего электростатического поля.
Носителями заряда в металлах являются электроны проводимости. Они возникают при конденсации паров металла за счет обобществления валентных электронов.
5.1. Напряженность и потенциал
электростатического поля в проводнике

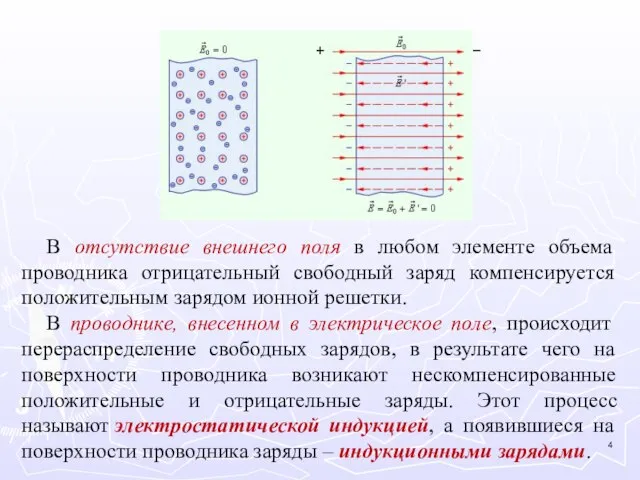
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки.
В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами.
+
−

В любой точке внутри проводника, находящимся в электростатическом поле Е = 0; dφ = 0; т. е. φ = const.
Диэлектрическая проницаемость εме → ∞.
На поверхности проводника напряженность направлена по нормали к этой поверхности, иначе, под действием составляющей Eτ, касательной к поверхности, заряды перемещались бы по проводнику, а это противоречило бы их статическому распределению.
Вне заряженного проводника – поле есть, следовательно, должен быть вектор , и направлен он перпендикулярно поверхности!

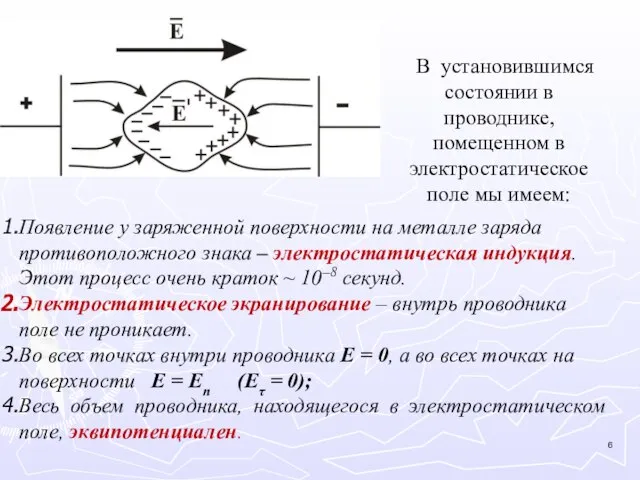
В установившимся состоянии в проводнике, помещенном в электростатическое поле мы имеем:
Появление у заряженной поверхности на металле заряда противоположного знака – электростатическая индукция. Этот процесс очень краток ~ 10–8 секунд.
Электростатическое экранирование – внутрь проводника поле не проникает.
Во всех точках внутри проводника Е = 0, а во всех точках на поверхности Е = En (Eτ = 0);
Весь объем проводника, находящегося в электростатическом поле, эквипотенциален.

Действительно, в любой точке внутри проводника,
следовательно, φ = const.
Поверхность проводника тоже эквипотенциальна:
(5.1.1)
(для любой линии на поверхности)
Потенциал поверхности равен потенциалу объема проводника.
В заряженном проводнике нескомпенсированные заряды, располагаются только на поверхности (их расталкивают кулоновские силы).
Доказательство:
Согласно теореме Остроградского – Гаусса суммарный заряд q внутри объема проводника равен нулю, так как Е = 0

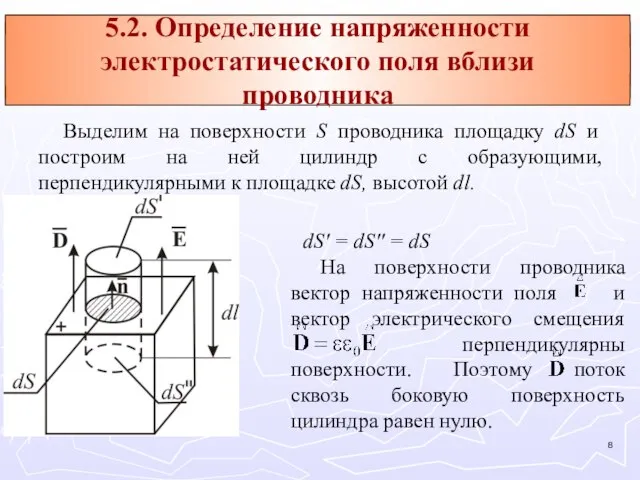
Выделим на поверхности S проводника площадку dS и построим на ней цилиндр с образующими, перпендикулярными к площадке dS, высотой dl.
dS' = dS'' = dS
На поверхности проводника вектор напряженности поля и вектор электрического смещения перпендикулярны поверхности. Поэтому поток сквозь боковую поверхность цилиндра равен нулю.
5.2. Определение напряженности
электростатического поля вблизи проводника

Поток вектора электрического смещения ФD через dS'' тоже равен нулю, так как dS'' лежит внутри проводника, где и, следовательно .
Отсюда следует, что поток dФD сквозь замкнутую поверхность равен потоку через dS':
dФD = DndS (5.2.1).
С другой стороны по теореме Остроградского-Гаусса: dФD = dq = σdS (5.2.2)
где: σ – поверхностная плотность зарядов на dS. Из равенства правых частей следует, что Dn = σ тогда
(5.2.3)
Напряженность поля вблизи поверхности заряженного проводника прямо пропорцианальна поверхностной плотности зарядов.

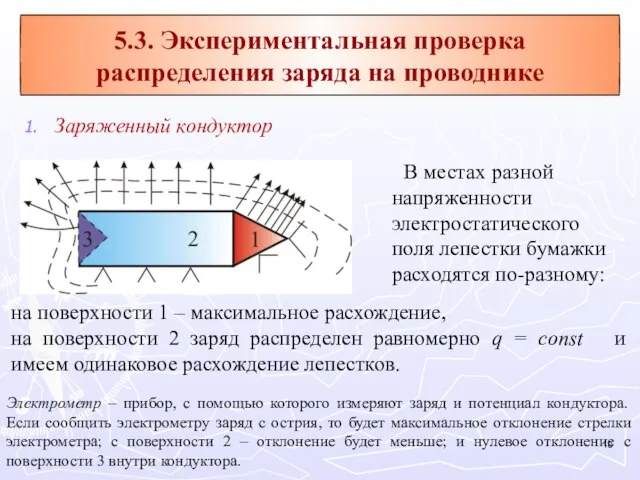
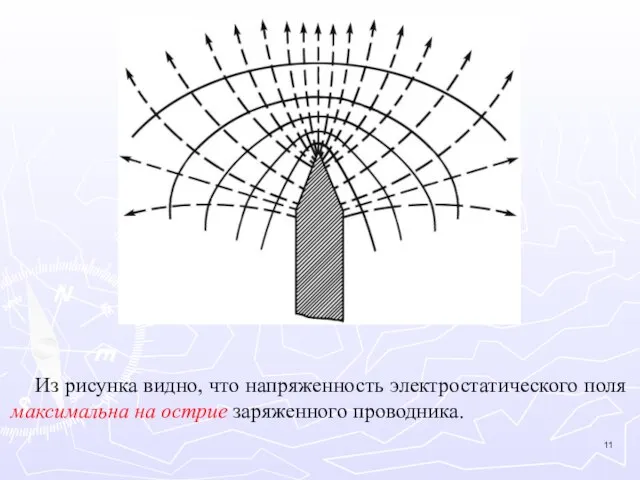
Заряженный кондуктор
В местах разной напряженности электростатического поля лепестки бумажки расходятся по-разному:
на поверхности 1 – максимальное расхождение,
на поверхности 2 заряд распределен равномерно q = const и имеем одинаковое расхождение лепестков.
Электрометр – прибор, с помощью которого измеряют заряд и потенциал кондуктора. Если сообщить электрометру заряд с острия, то будет максимальное отклонение стрелки электрометра; с поверхности 2 – отклонение будет меньше; и нулевое отклонение с поверхности 3 внутри кондуктора.
5.3. Экспериментальная проверка
распределения заряда на проводнике

Из рисунка видно, что напряженность электростатического поля максимальна на острие заряженного проводника.

2. Стекание электростатических зарядов с острия.
Большая напряженность поля E на остриях – нежелательное явление, т.к. происходит утечка зарядов и ионизация воздуха. Ионы уносят электрический заряд, образуется как бы «электрический ветер» («огни Святого Эльма»).
На острие заряженного проводника поверхностная плотность
заряда достигает большой величины. Электрическое поле вблизи
острия является сильным и резко неоднородным. При этом могут
происходить следующие явления.
Нейтральные молекулы воздуха поляризуются и притягиваются к
острию. Коснувшись острия, они заряжаются одноимённо с ним и
отталкиваются. Сила отталкивания превосходит ранее действовавшую силу притяжения, так как она действует на заряженные молекулы, а сила притяжения – на нейтральные. По этой причине молекулы удаляются от острия с большими скоростями, чем приближались к нему. Возникает поток заряженных частиц, направленный от острия («электрический ветер»). Это явление называют также «стеканием заряда с острия».

Есть наглядные эксперименты по этому явлению: сдувание пламени свечи электрическим ветром; колесо Франклина или вертушка. На этом принципе построен электростатический двигатель.
Прибор (рис. 2, 3) предназначен для демонстрации вращения легкой спицы за счет стекания электростатического заряда с ее заостренных концов.
Основные части прибора: спица из тонколистовой бронзы с заостренными концами и центральным опорным подшипником; стержень с острием на верхнем конце и отверстием диаметром 4 мм для подключения электрофорной машины; подставка .

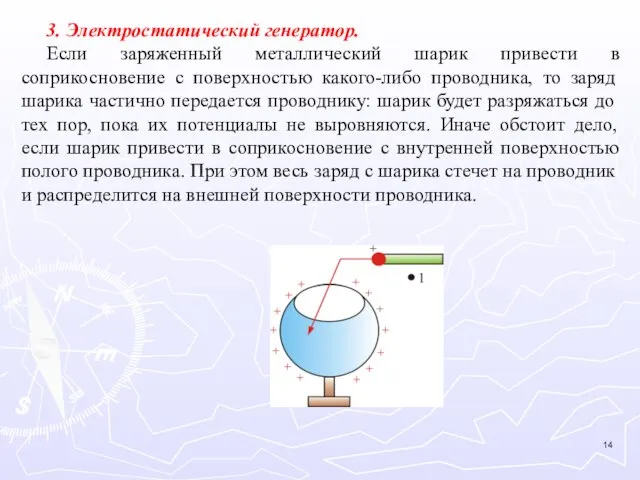
3. Электростатический генератор.
Если заряженный металлический шарик привести в соприкосновение с поверхностью какого-либо проводника, то заряд шарика частично передается проводнику: шарик будет разряжаться до тех пор, пока их потенциалы не выровняются. Иначе обстоит дело, если шарик привести в соприкосновение с внутренней поверхностью полого проводника. При этом весь заряд с шарика стечет на проводник и распределится на внешней поверхности проводника.

Рис. 5.4
Потенциал полого проводника может быть больше, чем потенциал шарика, тем не менее, заряд с шарика стечет полностью: В точке 1 φШ < φПР, но пока мы переносили шарик в полость, мы совершили работу по преодолению сил отталкивания, и тем самым, увеличивая потенциальную
энергию – увеличили потенциал шарика. То есть пока вносим шарик, потенциал его станет больше и заряд будет, как обычно, перетекать от большего потенциала к меньшому. Перенося с помощью шарика следующую порцию заряда, мы совершаем еще большую работу. Это наглядный пример того, что потенциал – энергетическая характеристика.

ВАН ДЕ ГРААФ Роберт
(1901 – 1967) - американский физик.
Окончил университет штата Алабама (1922). Совершенствовал знания в Сорбонне и Оксфорде. В 1929-1931 работал в Принстонском университете, в 1931 –1960 – в Массачусетском технологическом институте.
Научные исследования в области ядерной физики и ускорительной техники.
Выдвинул идею тандемного ускорителя и к 1958 построил первый тандемный ускоритель отрицательных ионов.
Изобрел в 1931 году высоковольтный электростатический ускоритель (генератор Ван де Граафа), спроектировал и построил генератор с диаметром сфер по 4,5 м.
В 1936 построил самый большой из традиционных генераторов постоянного напряжения.

Зарядное устройство заряжает ленту транспортера положительными зарядами. Лента переносит их вовнутрь сферы и там происходит съем положительных зарядов. Далее они стекают на внешнюю поверхность. Так можно получить потенциал относительно земли в несколько миллионов вольт –
ограничение – ток утечки. Такие генераторы существуют в настоящие время. Например, в Массачусетском технологическом институте построен генератор с диаметром сферы 4,5 метров и получен потенциал 3 ÷ 5·106 В.
В Томске очень развита ускорительная техника. Так, только в НИИ ядерной физики имеется около десяти ускорителей (генераторы различного класса). Один из них ЭСГ или генератор Ван-де-Граафа. Он изготовлен в специальной башне и на нем получали потенциал один миллион вольт.

5.4.1. Электрическая емкость
При сообщении проводнику заряда, на его поверхности появляется потенциал φ. Но если этот же заряд сообщить другому проводнику, то потенциал будет другой. Это зависит от геометрических параметров проводника. Но в любом случае, потенциал φ пропорционален заряду q.
q = C⋅φ (5.4.1)
Коэффициент пропорциональности называют электроемкостью – это физическая величина, численно равна заряду, который необходимо сообщить проводнику для того, чтобы изменить его потенциал на единицу. Единица измерения емкости в СИ – фарада 1 Ф = 1Кл / 1В.
5.4. Конденсаторы

Если потенциал поверхности шара
(5.4.3),
то
Cшар. = 4 πεε0R (5.4.4),
Если ε = 1 (воздух, вакуум) и R = Rземли, то
CЗ = 7·10 –4 Ф или 700 мкФ.
Чаще на практике используют и более мелкие единицы: 1 нФ (нанофарада) = 10–9 Ф и 1 пкФ (пикофарада) = 10 –12 Ф.
Необходимость в устройствах, накапливающих заряд есть, а уединенные проводники обладают малой емкостью. Обратите внимание, что электроемкость проводника увеличивается, если к нему поднести другой проводник – явление электростатической индукции.
Конденсатор – два проводника называемые обкладками расположенные близко друг к другу.

Конструкция такова, что внешние окружающие конденсатор тела не оказывают влияние на электроемкость конденсатора. Это будет выполняться, если электростатическое поле будет сосредоточено внутри конденсатора между обкладками.
Конденсаторы бывают плоские, цилиндрические и сферические.
Так как электростатическое поле находится внутри конденсатора, то линии электрического смещения начинаются на положительной обкладке и заканчиваются на отрицательной – и никуда не исчезают. Следовательно, заряды на обкладках противоположны по знаку, но одинаковы по величине.
Емкость конденсатора: (5.4.5)

Найдем формулу для емкости плоского конденсатора.
Напряженность между обкладками равна
(5.4.6)
где: S – площадь пластин (обкладок); q – заряд конденсатора
отсюда (5.4.7)
ε – диэлектрическая проницаемость диэлектрика между обкладками.
Как видно из формулы, диэлектрическая проницаемость вещества очень сильно влияет на емкость конденсатора. Это можно увидеть и экспериментально: заряжаем электроскоп, подносим к нему металлическую пластину – получили конденсатор (за счет электростатической индукции, потенциал увеличился).
.

Вносим между пластинами диэлектрик с ε, больше чем у воздуха и потенциал конденсатора изменяется.
Отсюда можно получить единицы измерения ε0:
Помимо емкости каждый конденсатор характеризуется Uраб (или Uпр. – максимальное допустимое напряжение).

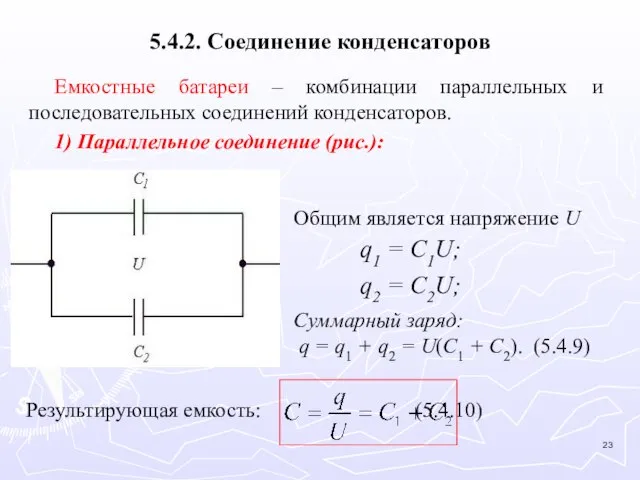
5.4.2. Соединение конденсаторов
Емкостные батареи – комбинации параллельных и последовательных соединений конденсаторов.
1) Параллельное соединение (рис.):
Общим является напряжение U
Суммарный заряд:
q = q1 + q2 = U(C1 + C2). (5.4.9)
Результирующая емкость: (5.4.10)

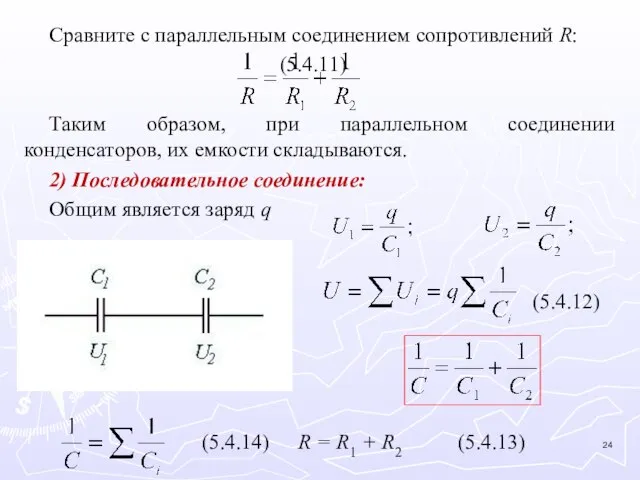
Сравните с параллельным соединением сопротивлений R:
(5.4.11)
Таким образом, при параллельном соединении конденсаторов, их емкости складываются.
2) Последовательное соединение:
Общим является заряд q
(5.4.12)
(5.4.14) R = R1 + R2 (5.4.13)

5.4.3. Расчет емкостей различных конденсаторов
Емкость плоского конденсатора.
где d = x2 – x1 – расстояние между пластинами.
Так как заряд q = σ⋅S, то
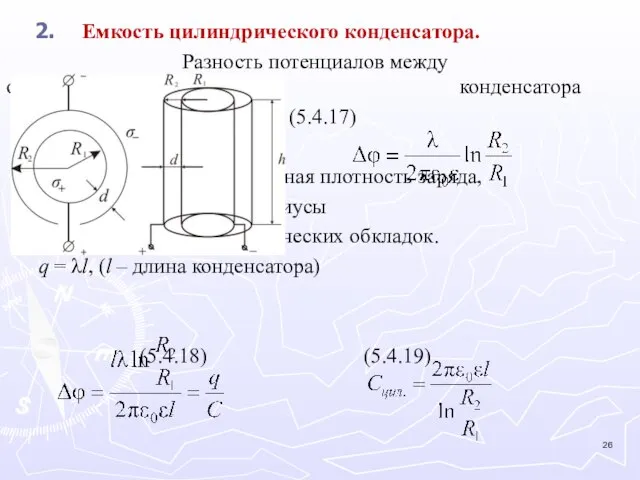
(5.4.16)
,

Емкость цилиндрического конденсатора.
Разность потенциалов между обкладками цилиндрического конденсатора
(5.4.17)
где λ – линейная плотность заряда,
R1и R2 – радиусы
цилиндрических обкладок.
q = λl, (l – длина конденсатора)
(5.4.18) (5.4.19)

Понятно, что зазор между обкладками мал: d = R2 – R1, то есть d << R1, тогда
(5.4.20)
3. Емкость шарового конденсатора.
(5.4.21)
Это разность потенциалов между обкладками шарового конденсатора, где R1 и R2 – радиусы шаров.
(5.4.22)

В шаровом конденсаторе R1 ≈ R2; S = 4πR2; R2 – R1 = d – расстояние между обкладками. Тогда
(5.4.23)
Таким образом, емкость шарового конденсатора,
что совпадает с емкостями плоского и цилиндрического конденсатора.

5.4.4. Энергия заряженного конденсатора
Если замкнуть обкладки конденсатора, то по проволоке потечет ток, который может даже расплавить ее. Значит, конденсатор запасает энергию. Вычислим ее.
Конденсатор разряжается U' – мгновенное значение напряжения на обкладках. Если при этом значении напряжения между обкладками проходит заряд dq, то работа
dA = U'dq. (5.4.24)
Работа равна убыли потенциальной энергии конденсатора:
dA = – dWc. (5.4.25)
Так как q = CU, то dA = CU'dU', а полная работа

(5.4.26)
(5.4.27)
Энергию конденсатора можно посчитать и по другим формулам:
(5.4.28)

В пределах электростатики дать ответ на вопрос «Где сосредоточена энергия конденсатора?» невозможно. Поля и заряды, их образовавшие не могут существовать обособленно. Их не разделить. Однако переменные поля могут существовать независимо от возбуждавших их зарядов (излучение солнца, радиоволны, …) и они переносят энергию. Эти факты заставляют признать, что носителем энергии является электростатическое поле.
Носителем энергии в конденсаторе, Wc является электростатическое поле. Найдем Wc:
5.5. Энергия электростатического поля
, Sd = V – объем. Отсюда:

(5.5.1)
Если поле однородно, заключенная в нем энергия распределяется в пространстве с постоянной плотностью. Тогда можно посчитать удельную энергию ωуд:
(5.5.2)
Или, так как D = ε0εE, то (5.5.3)
Эти формулы справедливы для однородного поля.
Если поле создано двумя точечными зарядами q1 и q2, то для каждого из них
W1 = q1 ⋅ϕ12; W2 = q2 ⋅ϕ21
Здесь φ12 – потенциал поля, создаваемого зарядом q2 в точке, где расположен заряд q1, φ21 – потенциал поля от заряда q1 в точке с зарядом q2.

Для вакуума можно записать
Здесь r – расстояние между зарядами. Из двух последних систем уравнений следует, что
Обобщая этот вывод на систему из N зарядов, записываем:
(5.5.4)
потенциал в точке, где расположен заряд q1,
создаваемый всеми остальными зарядами (кроме q1).