Содержание
- 2. 11.1. Опыты Резерфорда и ядерная модель атома В 1833 году при исследовании явления электролиза М. Фарадей
- 3. В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к массе. Опыты
- 4. Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и его сотрудниками Э.
- 5. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению
- 6. Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное
- 7. 11.2. Постулаты Бора. Экспериментальное подтверждение постулатов Бора Планетарная модель атома, предложенная Резерфордом, несомненно явилась крупным шагом
- 8. Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году выдающийся датский физик Н.
- 9. Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из одного стационарного состояния с
- 10. Постулаты Бора 1. Электрон в атоме может двигаться только по определенным стационарным орбитам, каждой из которых
- 11. Атом водорода. Линейчатые спектры Простейший из атомов, атом водорода явился своеобразным тест-объектом для теории Бора. Ко
- 12. Стационарные орбиты атома водорода и образование спектральных серий Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие
- 13. 11.3. Теория Бора для водородоподобных систем и её принципиальные недостатки Правило квантования, приводящее к правильным, согласующимся
- 14. Полная энергия электрона, движущегося по n-ой стационарной орбите, складывается из его кинетической энергии и потенциальной энергии
- 15. Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с энергией En на другую
- 16. Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были поразительны. Стало ясно, что
- 17. 11.4. Гипотеза де Бройля и её экспериментальные подтверждения Установление корпускулярно-волнового дуализма в оптических явлениях имело очень
- 18. Найдем длину волны де Бройля у макроскопического, но достаточно малого объекта - пылинки, масса которой m
- 19. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на
- 20. Экспериментальные подтверждения гипотезы де Бройля Первые экспериментальные исследования, подтвердившие волновую природу частиц, были выполнены американскими физиками
- 21. Дэвиссон и Джермер исследовали дифракцию электронов на монокристалле никеля, кристаллическая структура которого была известна из опытов
- 22. В опытах Дэвиссона и Джермера максимальное отражение электронов наблюдалось при ускоряющей разности потенциалов U = 54
- 23. В экспериментах Дж. Томсона исследовалась дифракция электронов на поликристаллическом образце. Коллимированный пучок моноэнергетических электронов падал нормально
- 24. Дифракция одиночных электронов Рассмотренные выше эксперименты проводились с достаточно интенсивными пучками частиц, в данном случае электронов.
- 26. Скачать презентацию
Слайд 211.1. Опыты Резерфорда и ядерная модель атома
В 1833 году при исследовании явления электролиза
11.1. Опыты Резерфорда и ядерная модель атома
В 1833 году при исследовании явления электролиза

Важным свидетельством сложной структуры атомов явились спектроскопические исследования, которые привели к открытию линейчатых спектров атомов. В начале XIX века были открыты дискретные спектральные линии в излучении атомов водорода в видимой части спектра, и впоследствии были установлены математические закономерности, связывающие длины волн этих линий (И. Бальмер, 1885 г.).
В 1896 году А. Беккерель обнаружил явление испускания атомами невидимых проникающих излучений, названное радиоактивностью. В последующие годы было обнаружено, что атомы радиоактивных веществ испускают три вида излучений различной физической природы (альфа-, бета- и гамма-лучи). Альфа-лучи оказались потоком ионов гелия. Бета-лучи – потоком электронов, а гамма-лучи – потоком квантов жесткого рентгеновского излучения.
Слайд 3В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к
В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к

Таким образом, на основании всех известных к началу XX века экспериментальных фактов можно было сделать вывод о том, что атомы вещества имеют сложное внутреннее строение. Они представляют собой электронейтральные системы, причем носителями отрицательного заряда атомов являются легкие электроны, масса которых составляет лишь малую долю массы атомов. Основная часть массы атомов связана с положительным зарядом.
Перед наукой встал вопрос о внутреннем строении атомов.
Первая попытка создания модели атома на основе накопленных экспериментальных данных принадлежит Дж. Томсону (1903 г.). Он считал, что атом представляет собой электронейтральную систему шарообразной формы радиусом примерно равным 10–10 м. Положительный заряд атома равномерно распределен по всему объему шара, а отрицательно заряженные электроны находятся внутри него. Для объяснения линейчатых спектров
испускания атомов Томсон пытался определить
расположение электронов в атоме и рассчитать частоты
их колебаний около положений равновесия. Однако
эти попытки не увенчались успехом.
Модель атома Дж. Томсона
Слайд 4Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и
Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и

Рассеяние, то есть изменение
направления движения α-частиц,
может вызвать только тяжелая
положительно заряженная часть
атома.
Схема опыта Резерфорда по рассеянию α-частиц.
K – свинцовый контейнер с радиоактивным веществом, Э – экран, покрытый сернистым цинком, Ф – золотая фольга, M – микроскоп.
Слайд 5Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами
Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами

Электрическое поле однородного заряженного шара максимально на его поверхности и убывает до нуля по мере приближения к центру шара. Если бы радиус шара, в котором сосредоточен весь положительный заряд атома, уменьшился в n раз, то максимальная сила отталкивания, действующая на α-частицу по закону Кулона, возросла бы в n2 раз. Следовательно, при достаточно большом значении n α-частицы могли бы испытать рассеяние на большие углы вплоть до 180°. Эти соображения привели Резерфорда к выводу, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвал атомным ядром. Так возникла ядерная модель атома.
Рассеяние α-частицы в атоме Томсона и в атоме Резерфорда
Слайд 6Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома
Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома
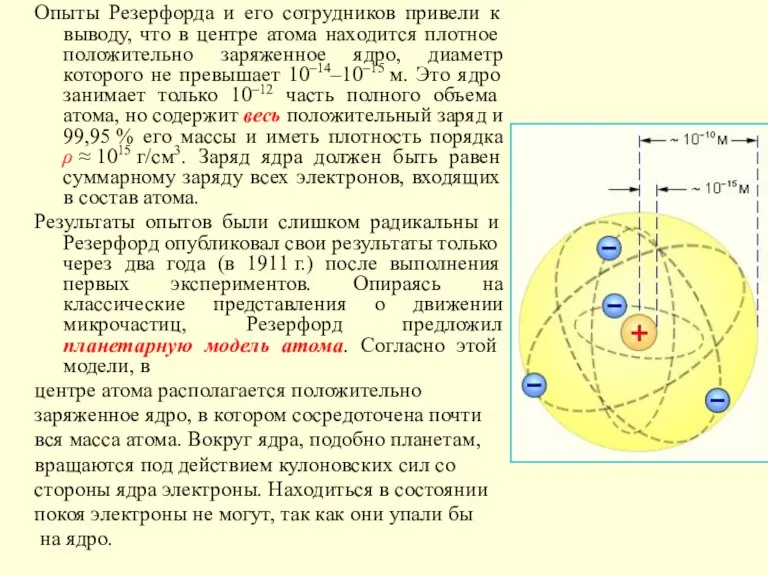
Результаты опытов были слишком радикальны и Резерфорд опубликовал свои результаты только через два года (в 1911 г.) после выполнения первых экспериментов. Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в
центре атома располагается положительно
заряженное ядро, в котором сосредоточена почти
вся масса атома. Вокруг ядра, подобно планетам,
вращаются под действием кулоновских сил со
стороны ядра электроны. Находиться в состоянии
покоя электроны не могут, так как они упали бы
на ядро.
Слайд 711.2. Постулаты Бора. Экспериментальное подтверждение постулатов Бора
Планетарная модель атома, предложенная Резерфордом, несомненно
11.2. Постулаты Бора. Экспериментальное подтверждение постулатов Бора
Планетарная модель атома, предложенная Резерфордом, несомненно

Слайд 8Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году выдающийся
Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году выдающийся

Первый постулат Бора (постулат стационарных состояний) гласит: атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает.
Этот постулат находится в явном противоречии с классической механикой, согласно которой энергия движущегося электрона может быть любой. Он находится в противоречии и с электродинамикой, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн. Согласно первому постулату Бора, атом характеризуется системой энергетических уровней, каждый из которых соответствует определенному стационарному состоянию. Механическая энергия электрона, движущегося по замкнутой траектории вокруг положительно заряженного ядра, отрицательна. Поэтому всем стационарным состояниям соответствуют значения энергии En < 0. При En ≥ 0 электрон удаляется от ядра (ионизация). Величина |E1| называется энергией ионизации. Состояние с энергией E1 называется основным состоянием атома.
Слайд 9Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из
Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из

Второй постулат Бора также противоречит электродинамике Максвелла, так как частота излучения определяется только изменением энергии атома и никак не зависит от характера движения электрона.
Теория Бора не отвергла полностью законы классической физики при описании поведения атомных систем. В ней сохранились представления об орбитальном движении электронов в кулоновском поле ядра. Классическая ядерная модель атома Резерфорда была дополнена в теории Бора идеей о квантовании электронных орбит. Поэтому теорию Бора иногда называют полуклассической.
Слайд 10Постулаты Бора
1. Электрон в атоме может двигаться только по определенным стационарным орбитам,
Постулаты Бора
1. Электрон в атоме может двигаться только по определенным стационарным орбитам,

2. Разрешенными стационарными орбитами являются только те, для которых угловой момент импульса L электрона равен целому кратному величины постоянной Планка ħ. Поэтому для n-ой стационарной орбиты выполняется условие квантования L = nħ, n = 1, 2, 3,…
3. Излучение или поглощение кванта излучения происходит при переходе атома из одного стационарного состояния в другое. При этом частота ω излучения атома определяется разностью энергий атома в двух стационарных состояниях, так что
ħωnk = Ek – En, k > n.
Слайд 11Атом водорода. Линейчатые спектры
Простейший из атомов, атом водорода явился своеобразным тест-объектом для
Атом водорода. Линейчатые спектры
Простейший из атомов, атом водорода явился своеобразным тест-объектом для

Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии (серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле называется постоянной Ридберга. Ее численное значение R = 3,29·1015 Гц. До Бора механизм возникновения линейчатых спектров и смысл целых чисел, входящих в формулы спектральных линий водорода (и ряда других атомов), оставались непонятными.
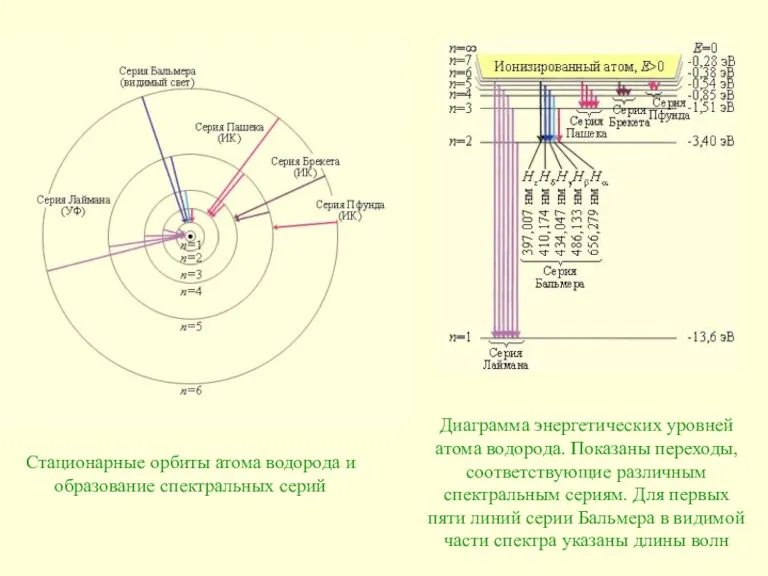
Слайд 12Стационарные орбиты атома водорода и образование спектральных серий
Диаграмма энергетических уровней атома
Стационарные орбиты атома водорода и образование спектральных серий
Диаграмма энергетических уровней атома
Слайд 1311.3. Теория Бора для водородоподобных систем и её принципиальные недостатки
Правило квантования, приводящее
11.3. Теория Бора для водородоподобных систем и её принципиальные недостатки
Правило квантования, приводящее

Запишем условие вращения электрона массы m0 по круговой орбите радиуса r под действием кулоновской силы со стороны ядра и формулу Бора квантования момента импульса электрона
Решая эту систему уравнений, находим для радиусов допустимых (стационарных) орбит электрона в атоме водорода следующее выражение
Вводя в качестве универсальной константы теории боровский радиус
как радиус первой стационарной орбиты электрона в атоме водорода, тогда
rn = an2, n = 1, 2, 3…
Слайд 14Полная энергия электрона, движущегося по n-ой стационарной орбите, складывается из его кинетической
Полная энергия электрона, движущегося по n-ой стационарной орбите, складывается из его кинетической

и потенциальной энергии кулоновского взаимодействия электрона с ядром
Получаем важную формулу теории Бора - формулу квантования энергии электрона в атоме водорода
Полная энергия электрона в атоме оказалась отрицательной, так как, по определению, отрицательна потенциальная электростатическая энергия взаимодействия электрона с ядром. С ростом номера орбиты полная энергия электрона в атоме возрастает. При этом номер орбиты n является квантовым числом в такой теории.
Слайд 15Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с
Согласно второму постулату Бора, при переходе электрона с одной стационарной орбиты с

Эта формула в точности совпадает с эмпирической формулой Ридберга для спектральных серий атома водорода, если положить постоянную R равной
Подстановка числовых значений me, e, ε0 и h в эту формулу дает результат
R = 3,29·1015 Гц,
который очень хорошо согласуется с эмпирическим значением R.
Слайд 16Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были
Успехи теории Бора в объяснении спектральных закономерностей в изучении атома водорода были

E2 – E1 = 4,9 эВ.
Согласно боровской концепции, при обратном самопроизвольном переходе атома ртуть должна испускать кванты с частотой
Спектральная линия с такой частотой действительно была обнаружена в ультрафиолетовой части спектра в излучении атомов ртути.
Слайд 1711.4. Гипотеза де Бройля и её экспериментальные подтверждения
Установление корпускулярно-волнового дуализма в оптических
11.4. Гипотеза де Бройля и её экспериментальные подтверждения
Установление корпускулярно-волнового дуализма в оптических

В 1924 г французский физик Луи де Бройль выдвинул гипотезу, согласно которой корпускулярно-волновой дуализм имеет универсальный характер. Согласно гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы остаются такими же, как и в случае электромагнитного излучения. Напомним, что энергия E и импульс p фотона связаны с круговой частотой ω и длиной волны λ соотношениями
E = ħω, p = kħ = 2πħ/λ.
По гипотезе де Бройля движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна ω = E/ħ, а длина волны
λБ = 2πħ/p
Как известно, плоская волна с частотой ω, распространяющаяся вдоль оси x, может быть представлена в комплексной форме
ξ(x,t) = Aexp[–i(ωt – kx)], где A – амплитуда волны, а k = 2π/λ – волновое число.
Согласно гипотезе де Бройля свободной частице с энергией E и импульсом p, движущейся вдоль оси x, соответствует плоская волна Ψ(x,t) = Aexp[–i(Et – px)/ħ], распространяющаяся в том же направлении и описывающая волновые свойства частицы. Эту волну называют волной де Бройля.
Слайд 18Найдем длину волны де Бройля у макроскопического, но достаточно малого объекта -
Найдем длину волны де Бройля у макроскопического, но достаточно малого объекта -

λБ = 2πħ/mυ = 6,6x10-22 м.
Найденная длина волны значительно меньше не только размеров самой пылинки, но и наименьшего известного в физике размера - радиуса ядра, составляющего по порядку величины 10-15 м.
Поскольку никакого принципиального различия между микро- и макрообъектами не существует, то возникает вопрос: в каких случаях волновые свойства играют решающую роль в поведении частицы, а в каких случаях они оказываются несущественными и их можно не учитывать? Для того, чтобы ответить на этот вопрос, воспользуемся аналогией с оптикой. Как известно, волновая природа излучения максимальным образом проявляется в тех случаях, когда длина волны излучения λ сравнима с характерными размерами системы L, т.е. λ ~ L. Если же λ << L, то волновые свойства излучения становятся несущественными и можно пользоваться геометрической или лучевой оптикой.
В силу аналогии, существующей между механическими и оптическими явлениями, классическая ньютоновская механика соответствует геометрической оптике, а квантовая или, как ее еще называют, волновая механика - волновой оптике. Таким образом, волновые свойства частиц будут наиболее ярко проявляться в тех случаях, когда дебройлевская длина волны частицы сравнима с характерными размерами области движения частицы L, т.е. λБ ~ L. Дебройлевская длина волны электрона λБ, размеры атома и расстояние между атомами в кристалле имеют один и тот же порядок величины. Это означает, что при взаимодействии электронов с атомами, а также при их движении в твердых телах волновые свойства электронов будут проявляться максимальным образом. В тех же случаях, когда λБ << L, как, например, для рассмотренной выше пылинки, волновые свойства частицы становятся несущественными, и для описания движения таких объектов необходимо пользоваться законами классической механики.
Слайд 19Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием
Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано десятилетием

В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ, т.е.
nλn = 2πrn.
Подставляя в это соотношение длину волны
де Бройля λ = h/p, где p = meυ – импульс электрона,
получим:
Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая n = 4
Слайд 20Экспериментальные подтверждения гипотезы де Бройля
Первые экспериментальные исследования, подтвердившие волновую природу частиц,
Экспериментальные подтверждения гипотезы де Бройля
Первые экспериментальные исследования, подтвердившие волновую природу частиц,

Слайд 21Дэвиссон и Джермер исследовали дифракцию электронов на монокристалле никеля, кристаллическая структура которого
Дэвиссон и Джермер исследовали дифракцию электронов на монокристалле никеля, кристаллическая структура которого
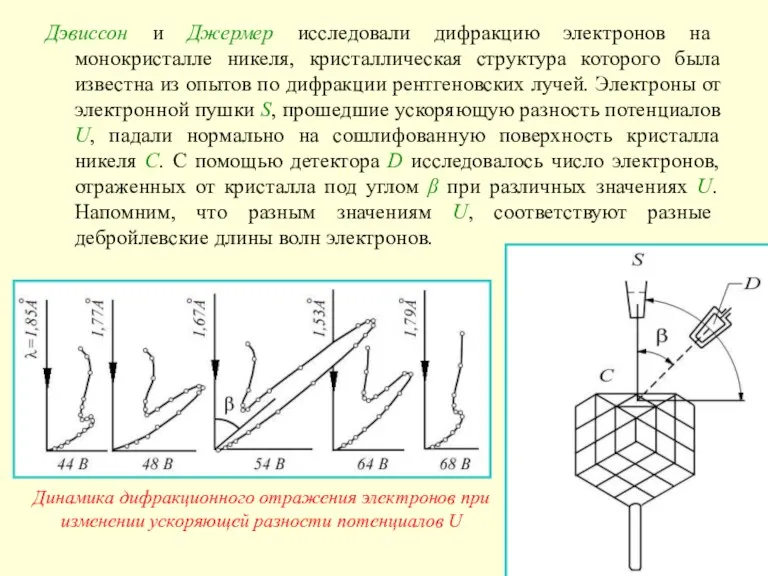
Динамика дифракционного отражения электронов при изменении ускоряющей разности потенциалов U
Слайд 22В опытах Дэвиссона и Джермера максимальное отражение электронов наблюдалось при ускоряющей разности
В опытах Дэвиссона и Джермера максимальное отражение электронов наблюдалось при ускоряющей разности
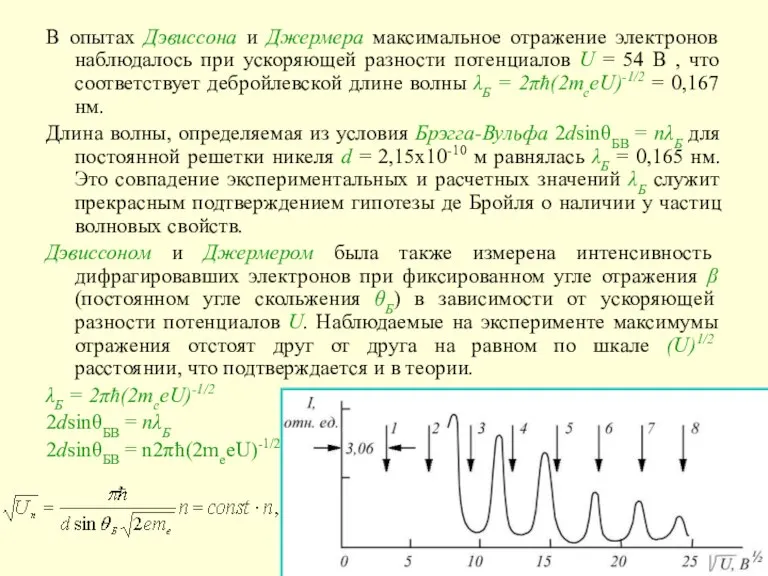
Длина волны, определяемая из условия Брэгга-Вульфа 2dsinθБВ = nλБ для постоянной решетки никеля d = 2,15x10-10 м равнялась λБ = 0,165 нм. Это совпадение экспериментальных и расчетных значений λБ служит прекрасным подтверждением гипотезы де Бройля о наличии у частиц волновых свойств.
Дэвиссоном и Джермером была также измерена интенсивность дифрагировавших электронов при фиксированном угле отражения β (постоянном угле скольжения θБ) в зависимости от ускоряющей разности потенциалов U. Наблюдаемые на эксперименте максимумы отражения отстоят друг от друга на равном по шкале (U)1/2 расстоянии, что подтверждается и в теории.
λБ = 2πħ(2meeU)-1/2
2dsinθБВ = nλБ
2dsinθБВ = n2πħ(2meeU)-1/2
Слайд 23В экспериментах Дж. Томсона исследовалась
дифракция электронов на поликристаллическом
образце. Коллимированный пучок
В экспериментах Дж. Томсона исследовалась
дифракция электронов на поликристаллическом
образце. Коллимированный пучок
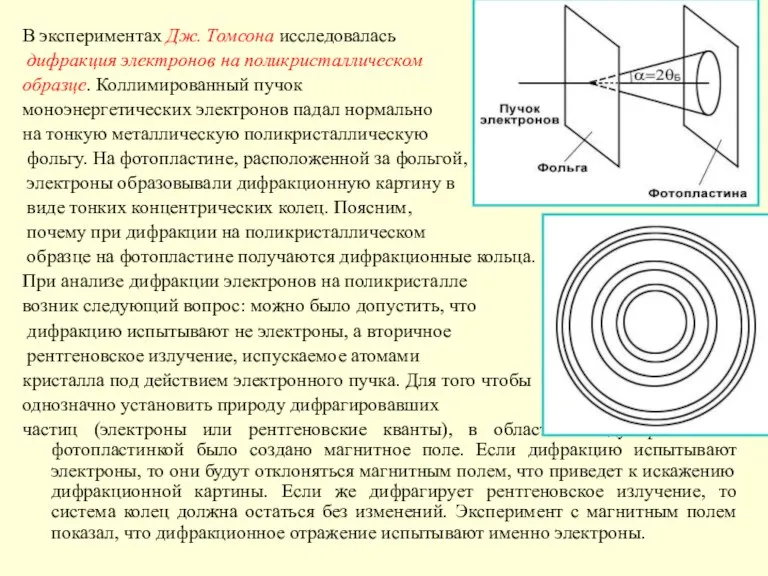
моноэнергетических электронов падал нормально
на тонкую металлическую поликристаллическую
фольгу. На фотопластине, расположенной за фольгой, прошедшие
электроны образовывали дифракционную картину в
виде тонких концентрических колец. Поясним,
почему при дифракции на поликристаллическом
образце на фотопластине получаются дифракционные кольца.
При анализе дифракции электронов на поликристалле
возник следующий вопрос: можно было допустить, что
дифракцию испытывают не электроны, а вторичное
рентгеновское излучение, испускаемое атомами
кристалла под действием электронного пучка. Для того чтобы
однозначно установить природу дифрагировавших
частиц (электроны или рентгеновские кванты), в области между фольгой и фотопластинкой было создано магнитное поле. Если дифракцию испытывают электроны, то они будут отклоняться магнитным полем, что приведет к искажению дифракционной картины. Если же дифрагирует рентгеновское излучение, то система колец должна остаться без изменений. Эксперимент с магнитным полем показал, что дифракционное отражение испытывают именно электроны.
Слайд 24Дифракция одиночных электронов
Рассмотренные выше эксперименты проводились с достаточно
интенсивными пучками частиц, в
Дифракция одиночных электронов
Рассмотренные выше эксперименты проводились с достаточно
интенсивными пучками частиц, в

Поэтому выявленные в них волновые свойства могли быть
приписаны как ансамблю взаимодействующих между собою
электронов, так и отдельному электрону. Для того, чтобы
выяснить, обладает ли индивидуальная частица волновыми
свойствами, группа отечественных физиков во главе с В.А.
Фабрикантом выполнила в 1949 г дифракционные исследования
с очень слабым пучком электронов. В этих опытах промежуток
времени между двумя последовательными прохождениями
электронов через кристалл в 30000 раз превышал время,
затрачиваемое одним электроном на прохождение всего прибора.
Таким образом, электроны дифрагировали в кристалле
поодиночке и полностью исключалось взаимодействие
электронов друг с другом как причина возникновения
дифракционной картины. При небольшой длительности
эксперимента точки на фотопластинке, отвечающие попаданию
электронов, распределены совершенно случайным образом. Однако при достаточной длительности эксперимента распределение точек приобретает характерный для дифракции на поликристалле вид концентрических колец. Таким образом было доказано, что волновые свойства присущи отдельному электрону.
 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота