Содержание
- 2. 1. Случайные события. Мера их неопределенности. Формула Хартли. 2. Энтропия по Шеннону. Свойства энтропии. 3. Условная
- 3. ЦЕЛИ КУРСА «ЭНТРОПИЯ И ИНФОРМАЦИЯ. РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ» Развитие логического мышления и формирование базы математических знаний;
- 4. Задачи курса: Расширить представления учащихся о дискретной математике, ее возможностях при вполне жизненных ситуациях; Ввести новые
- 5. В результате освоения данного курса ученик должен научиться: Различать количественные характеристики случайного события: вероятность и степень
- 6. Занятие №1. Случайные события. Мера их неопределенности. Формула Хартли. Цель занятия: Вспомнить понятие случайных событий; Ввести
- 7. Занятие №1. Случайные события. Мера их неопределенности. Формула Хартли. Задачи занятия: Научиться среди предложенных событий выбирать
- 8. Степень неопределенности – есть еще одна характеристика случайного события, которую назвали энтропией. (Н(α)). За единицу энтропии
- 9. Формула Хартли Пусть опыт α имеет k равновозможных исходов, тогда Этой формулой удобно пользоваться, когда исходы
- 10. Чем больше равновероятных исходов, тем больше степень неопределенности Чем меньше вероятность, тем больше степень неопределенности Что
- 11. ПРИЛОЖЕНИЕ №2.
- 12. Занятие №2. Энтропия по Шеннону. Свойства энтропии. Цели занятия: Продолжить усвоение понятия энтропия и ее свойств
- 13. Где вероятности равновозможных исходов. Он же предложил назвать эту величину энтропией Клод Шеннон
- 14. Имеются 2 урны. Первая содержит 20 шаров – 10 белых, 5 черных и 5 красных; Вторая
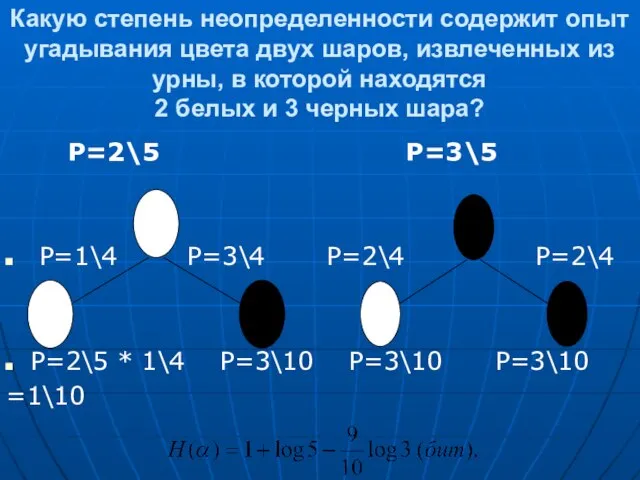
- 15. Какую степень неопределенности содержит опыт угадывания цвета двух шаров, извлеченных из урны, в которой находятся 2
- 16. Занятие №3. Условная энтропия. Решение задач на условную энтропию. Цель занятия: введение понятия условной энтропии для
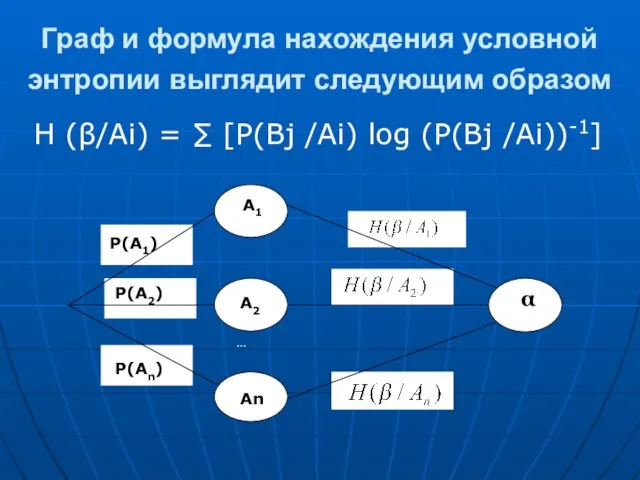
- 17. Граф и формула нахождения условной энтропии выглядит следующим образом Н (β/Аi) = ∑ [Р(Вj /Аi) log
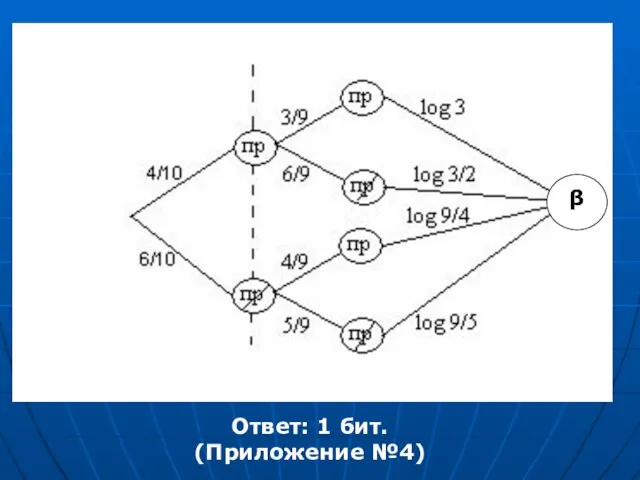
- 18. Какую энтропию содержит опыт угадывания простой цифры при извлечении из цифровой азбуки при условии, что одна
- 19. β Ответ: 1 бит. (Приложение №4)
- 20. Занятие №4. Количество информации. Решение задач Цель занятия: Введение понятия количества информации для решения задач Задачи
- 21. КОЛИЧЕСТВО ИНФОРМАЦИИ Количество информации I(α,β) показывает, насколько осуществление опыта α уменьшает неопределенность β т.е. как много
- 22. Свойства количества информации 0 ≤I(β/α) ≤ Н(β) I(α,β) = Н(α) + Н(β) - Н(α*β), I(α,β) =
- 23. Решение логических задач на взвешивание через энтропию и количество информации.
- 24. ЗАДАЧИ НА ВЗВЕШИВАНИЕ Задача: Имеется 12 монет одного достоинства, одна из которых фальшивая, отличающаяся от других
- 25. Решение: т.е. определение фальшивой монеты связано с получением информации, измеряющейся числом log24 или k*log3≥log24 Отсюда и
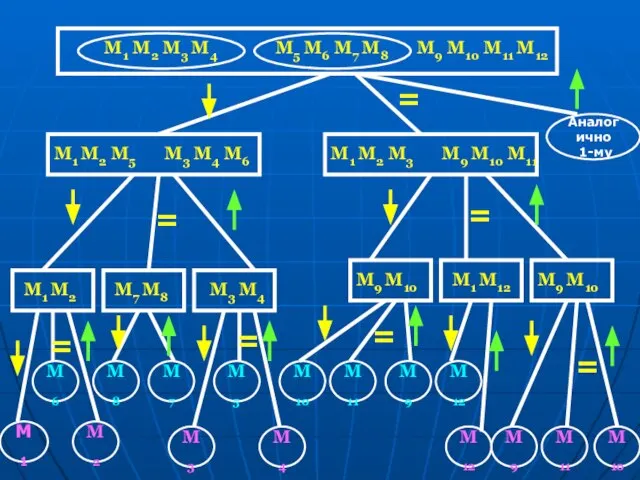
- 26. M1 M2 M3 M4 M5 M6 M7 M8 M9 M10 M11 M12 = M3 M4 M6
- 28. Скачать презентацию





















 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр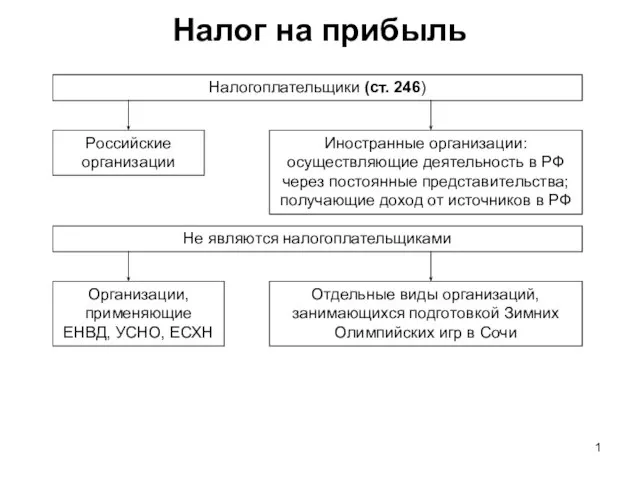 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология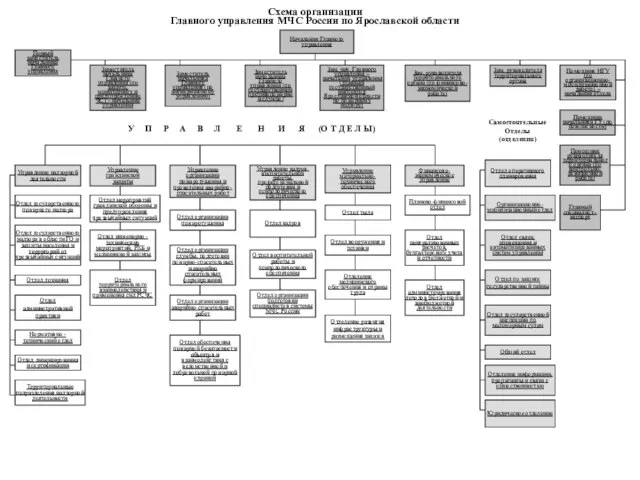 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва