Геометрический смысл производной

Использование геометрического смысла производной при решении задач.

Найдите угловой коэффициент касательной к графику функции y= 2x+eх в его точке с абсциссой xo=0.
Решение. Угловой коэффициент касательной к графику функции в точке с абсциссой xo равен значению производной функции в точке xo.Найдем производную y`=2+ex и её значение в точке xo=0, т.е. 2+eo=2+1=3.
Ответ: 3.

Найдите тангенс угла наклона касательной к графику функции y=7x-5sinx в точке с абсциссой xo=π/2.
Решение. Тангенс угла наклона касательной к графику функции в точке с абсциссой xo равен значению производной функции в точке xo. Найдем производную y`=7-5cosx и значение производной в точке xo= π/2, т.е. y`(π/2)=7-5cos(π/2)=7-0=7.
Ответ: 7.

Найдите т. xo ,если тангенс угла наклона касательной, проведенной к графику функции y=3x2-7x+5 в точке с абсциссой xo , равен 2.
Решение. Так как тангенс угла наклона касательной к графику функции в точке с абсциссой xo равен значению производной функции в точке xo, то tgα= y`(xo )=2. Найдем производную y`=6x-7 и решим уравнение
6 xo-7=2
xo=1,5.
Ответ: 1,5.

Пусть касательная к графику функции y= f(x), проведенная в т. М(-2;-9) параллельна прямой 28x-4y+420=0. Найдите значение производной
f '(-2).
Решение. Значение производной f ' (-2) это угловой коэффициент касательной к графику функции y= f(x) в т. М(-2;-9). Так как эта касательная параллельна прямой 28x-4y+420=0, то их угловые коэффициенты равны.
Найдём угловой коэффициент прямой:
28x-4y+420=0, 4y=28x=420, y=7x+105. k=7=kкас = f ' (-2).
Ответ: 7.

В8. На рисунке изображен график производной функции y=f (x).
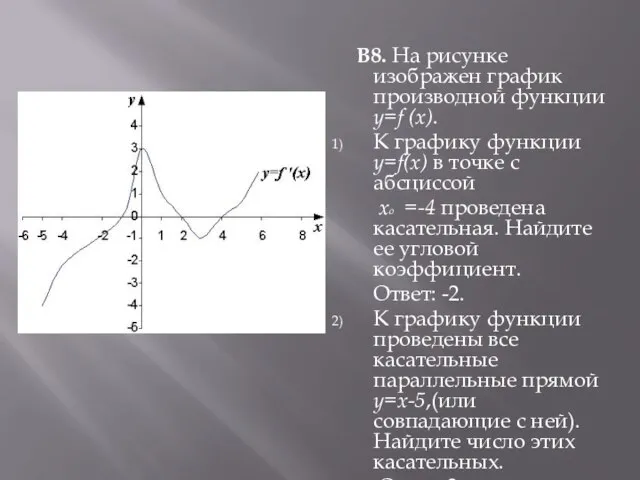
К графику функции y=f(x) в точке с абсциссой
xo =-4 проведена касательная. Найдите ее угловой коэффициент.
Ответ: -2.
К графику функции проведены все касательные параллельные прямой y=x-5,(или совпадающие с ней). Найдите число этих касательных.
Ответ: 3.