Геометрия три-тканей на плоскости

Постановка задачи
Цель работы: исследование некоторых вопросов геометрии три-тканей на плоскости.
Задачи:
Рассмотрение специфических свойств три-тканей на плоскости;
Исследование взаимосвязи геометрических и алгебраических свойств три-тканей на плоскости.

Задача 2. Найти уравнение прямолинейной три-ткани.
Решение. Уравнения семейств
прямых, образующих ткань:
- параметр прямой в семействе
Исключив x и y, получим:

Квазигруппы
Множество ,вместе с
называется группоидом.
Определение. Группоид называется квазигруппой, если
a)
b)

Абстрактные три-ткани
Пусть дано множество M, элементы -точки, и множества X,Y ,Z , элементы - линии первого, второго и третьего семейства, соответственно.

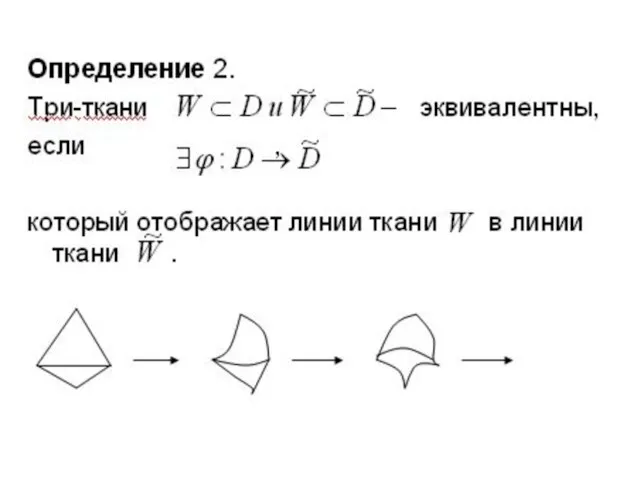
Определение. Множества M, X,Y, Z образуют абстрактную три-ткань если элементы этих множеств связаны отношением инцидентности, которое :
А1. Каждая точка множества M инцидентна в точности трем линиям, взятым по одной из семейств X,Y ,Z.
А2. Каковы бы ни были две линии, взятые из разных семейств, существует единственная точка из множества M инцидентная этим линиям.

Координатная квазигруппа
Рассмотрим три-ткань , образованную тремя семействами параллельных прямых. Определим операцию
следующим образом
Тогда трехбазисная квазигруппа называется координатной квазигруппой

Фигуры замыкания
На абстрактных три-тканях можно рассматривать различные фигуры замыкания – шестиугольные фигуры, фигуры Томсена и другие. Замыканию фигур определенного типа на ткани соответствует некоторое тождество, выполняемое в координатной квазигруппе .