Golden ratio

What is Golden Ratio?
The Golden Ratio is a unique number, approximately 1.618033989. It is also known as the Divine Ratio, the Golden Mean, the Golden Number, and the Golden Section.

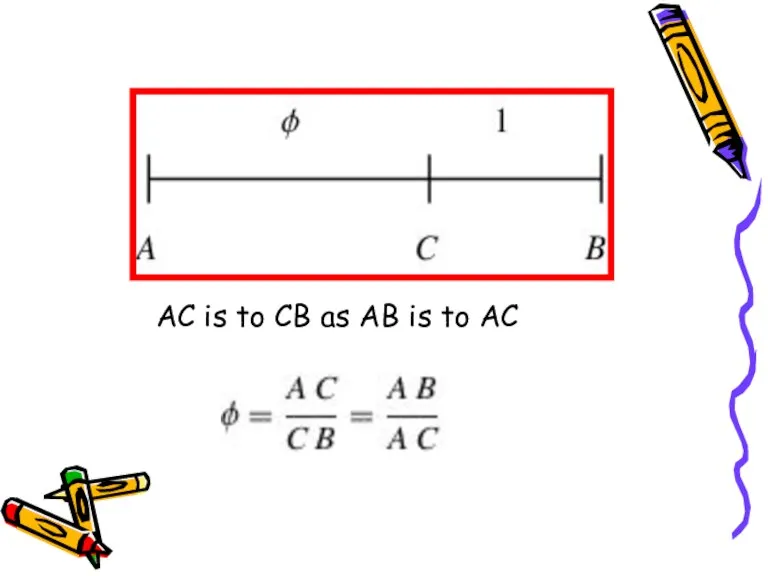
AC is to CB as AB is to AC

What is the Fibonacci Sequence of Numbers?
The Fibonacci numbers are a unique sequence of integers, starting with 1, where each element is the sum of the two previous numbers. For example: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.

Relationship between the Fibonacci Sequence and the Golden Ratio
The Fibonacci Sequence is an infinite sequence, which means it goes on for ever, and as it develops, the ratio of the consecutive terms converges (becomes closer) to the Golden Ratio, ~1.618. For example, to find the ratio of any two successive numbers, take the latter number and divide by the former. So, we will have: 1/1=1, 2/1=2, 3/2=1.5, 5/3=1.66, 8/5=1.6, 13/8=1.625, 21/13=1.615.

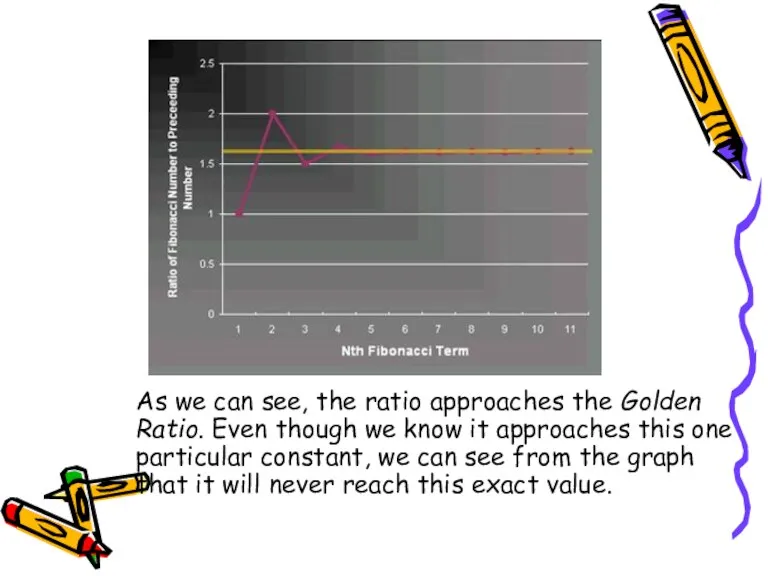
As we can see, the ratio approaches the Golden Ratio. Even though we know it approaches this one particular constant, we can see from the graph that it will never reach this exact value.

Algebraic properties of the Golden Proportion
1)
2)
3)

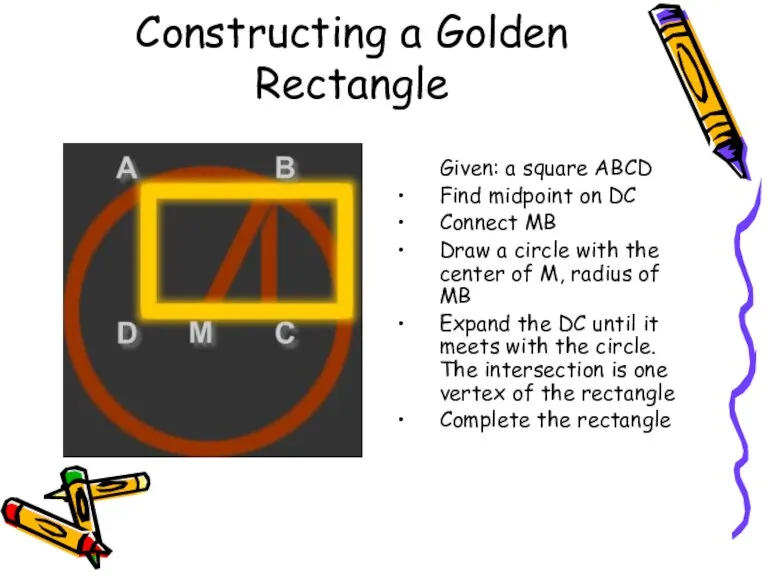
Constructing a Golden Rectangle
Given: a square ABCD
Find midpoint on DC
Connect MB
Draw a circle with the center of M, radius of MB
Expand the DC until it meets with the circle. The intersection is one vertex of the rectangle
Complete the rectangle

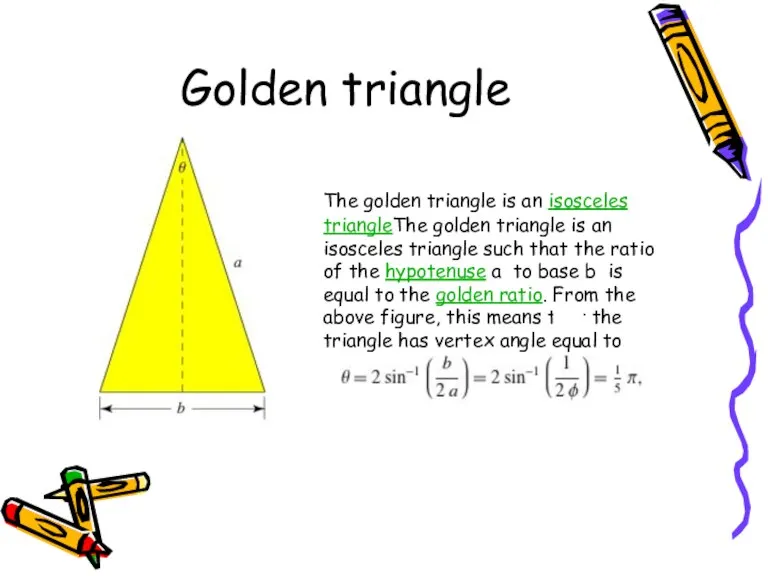
Golden triangle
The golden triangle is an isosceles triangleThe golden triangle is an isosceles triangle such that the ratio of the hypotenuse a to base b is equal to the golden ratio. From the above figure, this means that the triangle has vertex angle equal to

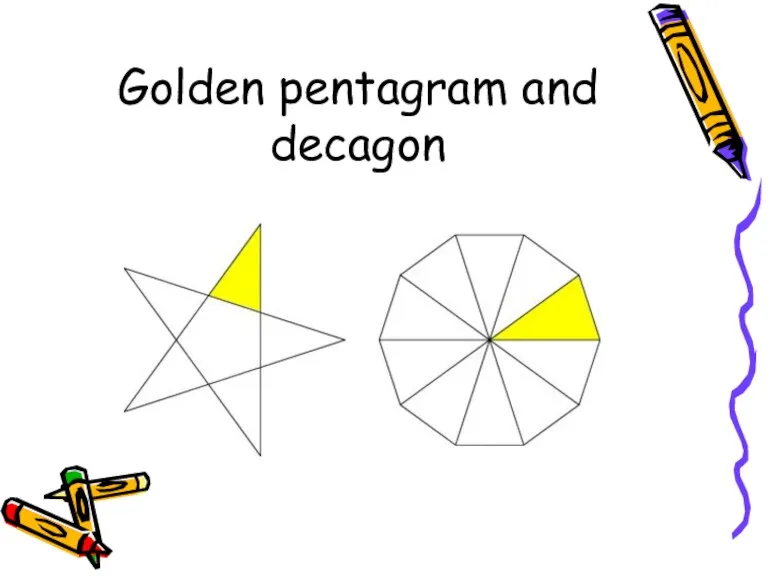
Golden pentagram and decagon

Plants growth
The branching rates in plants occur in the Fibonacci pattern, where the first level has one "branching" (the trunk), the second has two branches, than 3, 5, 8, 13 and so on. Also, the spacing of leaves around each branch or stalk spirals with respect to the Golden Ratio.

Flowers
On the back of the passiflora incarnate, the 3 sepals (the part of the flower that is not the petal) that protected the bud are outermost, followed by the 5 outer green petals and an inner layer of 5 more paler green petals.

Petal counts
The petals of the different flowers also contain the Fibonacci Numbers. The examples are that the buttercup has 5 petals, delphiniums has 8 petals, ragwort has 13 petals, aster as 21 petals, plantain has 34 petals, and asteraceae family has 55 petals, and some of them have 89 petals.

The Golden Ratio in Humans
Dr. Stephen Marquardt is a former plastic surgeon, has used the golden section and some of its relatives to make a mask that he claims that is the most beautiful shape a human face can ever have, it used decagons and pentagons as its function that embodies phi in all their dimensions.

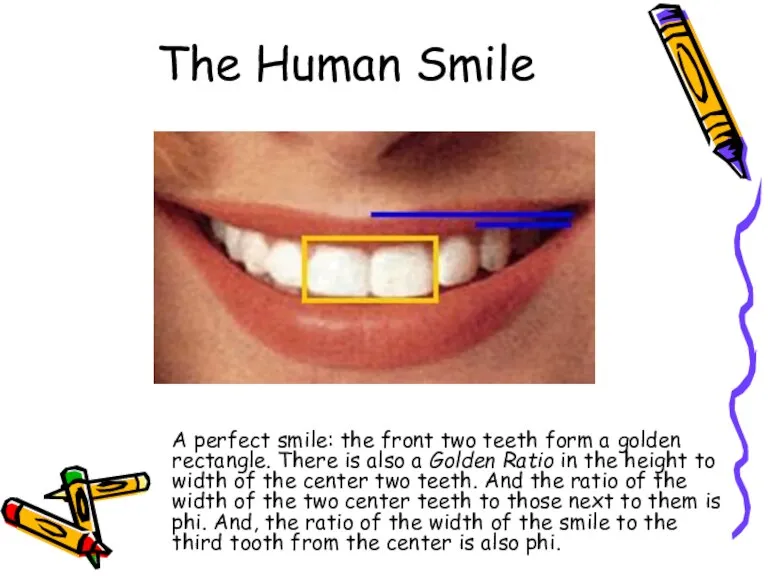
The Human Smile
A perfect smile: the front two teeth form a golden rectangle. There is also a Golden Ratio in the height to width of the center two teeth. And the ratio of the width of the two center teeth to those next to them is phi. And, the ratio of the width of the smile to the third tooth from the center is also phi.

The Golden Ratio in Arts
The Golden Ratio has a great impact on art, influencing artists' perspectives of a pleasant art piece. Da Vinci, a sculpture, a painter, an inventor and a mathematician, was the first one who first called Phi the Golden Ratio.

Mona Lisa
Mona Lisa's face is a perfect golden rectangle, according to the ratio of the width of her forehead compared to the length from the top of her head to her chin.

The last supper
The masterpiece "Last Supper," contains a golden ratio in several places, appearing in both the ceiling and the position where the people sit.

Statue of Athena
In the Statue of Athena, the first Golden Ratio is the length from the front head to the ear opening compared with the length from the forehead to the chin. The second one appears in the ratio of the length from the nostril to the earlobe compare with the length from the nostril to the chin.

The Golden Ratio in Architecture
The Golden Ratio has appeared in ancient architecture. Not only did the ancient Egyptians and Greeks know about the magic of Golden Ratio, so did the Renaissance artists, who used the Golden Ratio in the design of Notre Dame in between the 12th and 14th centuries.

The Great Pyramid at Giza
Half of the base, the slant height, and the height from the vertex to the center create a right triangle.

The Parthenon
The exterior dimensions of the Parthenon form a Golden Ratio in many of the proportions.

The UN Building
In the United Nations building, the width of the building compared with the height of every ten floors is a Golden Ratio.