Интерполяция и аппроксимация функций

Таблично-заданная функция:
Достоинство:
Нет необходимости проводить дополнительные расчеты значения функции.
Недостаток:
Невозможность определения значений функции при значениях аргумента, отличных от табличных.

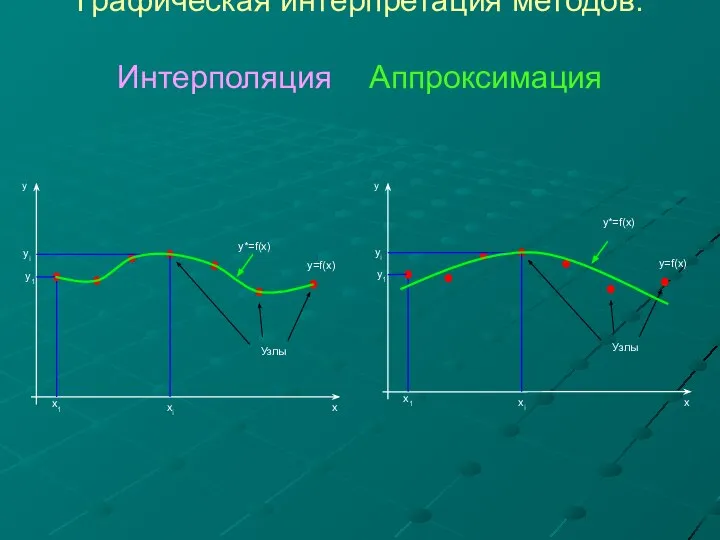
Графическая интерпретация методов:
Интерполяция Аппроксимация

1. Интерполяция функций
А) Глобальная интерполяция.
Б) Локальная интерполяция.

Локальная интерполяция
Необходимо определиться с видом интерполирующей функции.
На практике чаще всего использую следующие виды локальной интерполяции:
1. Линейная интерполяция
2. Квадратичная интерполяция
3. Сплайн-интерполяция

Глобальная интерполяция
Необходимо, чтобы одна интерполирующая функция проходила через все узлы таблично заданной функции.
Обычно в этом случае интерполирующую функцию ищут в виде полинома:
y=c0+c1x+c2x2 +…+cixi+…+cn-1xn-1
Через n точек может проходить только один график функции полинома n-1 порядка.

Интерполяция методом канонических полиномов
В уравнение полиномиальной зависимости подставляются все значения точек x - y (аргумент - функция) табличной зависимости.
Таким образом, получается система линейных уравнений n-го порядка:

Решаем полученную СЛАУ одним из известных методов, получаем значения параметров полиномиальной зависимости:
c0, c1, c2,…, ci,…, cn-1
В полученное уравнение полиномиальной функции с найденными параметрами подставляем значение аргумента xц и находим значение функции yц.
Данный метод удобен в случаях, когда необходимо найти несколько значений функции при нескольких значениях аргумента.

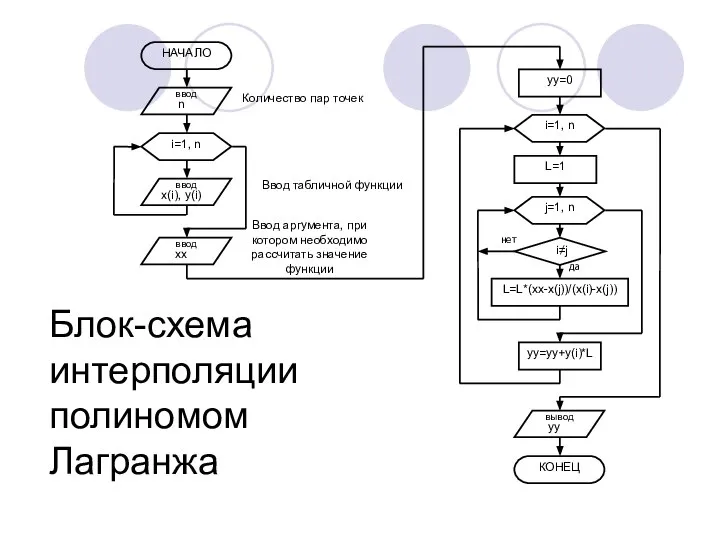
Интерполяция методом полинома Лагранжа
Данный метод удобен в случаях, когда необходимо найти только одно значение функции при одном значении аргумента.
В этом методе полином n-1 степени представляется в виде:
где l1, l2, …, li, …, ln - являются также полиномиальными зависимостями.

Данные полиномы рассчитываются по следующим формулам:
Коэффициент li будет равен 1, если xц=xi , и будет равен 0 (нулю), если xц= x1 , x2 и так далее.

Блок-схема интерполяции полиномом Лагранжа

Достоинства метода интерполяции:
Если исходная таблично заданная функция не содержит в себе погрешности, то метод интерполяции дает достаточно точные и достоверные результаты.
Недостатки метода интерполяции:
1. В случае локальной интерполяции получается несколько интерполирующих функций, с которыми неудобно работать.
2. В случае глобальной интерполяции при достаточно большом количестве пар точек (узлов) получается достаточно сложная и громоздкая интерполирующая функция.
3. Если исходная таблично заданная функция содержит в себе погрешность, то интерполирующая функция также будет «копировать» эту погрешность и не даст необходимого достоверного результата.

2. Аппроксимация функций
Всех перечисленных недостатков интерполяции лишен метод аппроксимации функций.
Аппроксимирующая функция не проходит через все узлы, а лежит максимально близко к ним.
В этом методе в случае флуктуаций (выбросов) точек, аппроксимирующая функция получается достаточно гладкой.

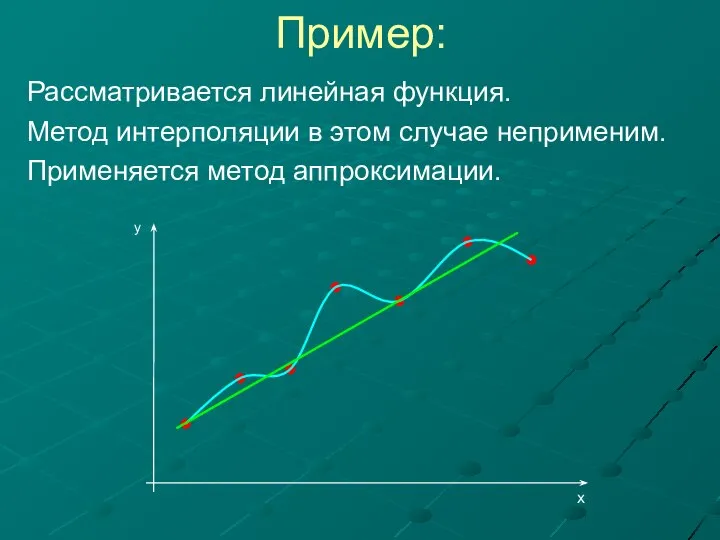
Пример:
Рассматривается линейная функция.
Метод интерполяции в этом случае неприменим.
Применяется метод аппроксимации.

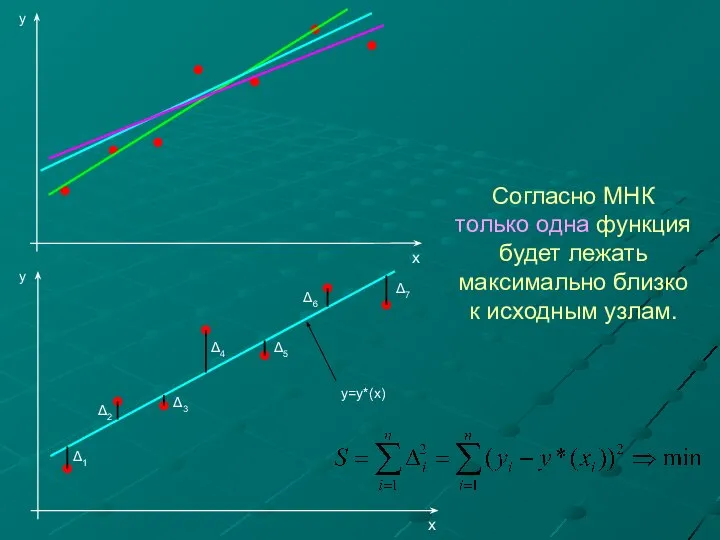
Возникает вопрос:
Каков критерий близости аппроксимирующей функции к исходной таблично заданной?
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК).
Суть: Аппроксимирующая функция должна быть такой, чтобы сумма квадратов отклонений аппроксимирующей функции от исходной таблично заданной была минимальной.

Согласно МНК только одна функция будет лежать максимально близко к исходным узлам.

Замечание:
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ не позволяет определить вид аппроксимирующей функции.
МНК позволяет определить только параметры выбранного вида аппроксимирующей функции.
Вид аппроксимирующей функции определяет пользователь исходя из теоретических знаний, логических предпосылок или других разумных соображений.

Аппроксимация линейной функцией
В качестве аппроксимирующей выбирают линейную функцию: y*=c0+c1x.
Здесь c0 и c1 - параметры функции, которые определим с использованием МНК.

В формулу суммы квадратов отклонений подставим аппроксимирующую линейную функцию, получим:
Находим минимум функции S,приравняв частные производные функции S по параметрам аппроксимирующей функции нулю:

Преобразуем полученные выражения:
В результате получаем СЛАУ, где в качестве неизвестных выступают параметры линейной функции c0 и c1:

Решаем полученную СЛАУ методом Крамера:
Таким образом, вычислив параметры c0 и c1, мы получаем линейную аппроксимирующую функцию:
y*=c0+c1x.

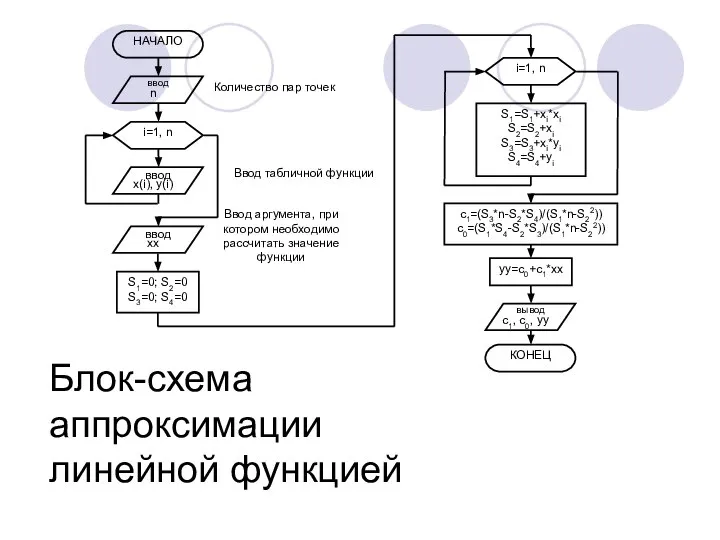
Блок-схема аппроксимации линейной функцией

Аппроксимация квадратичной функцией
В качестве аппроксимирующей выбирают квадратичную функцию: y*=c0+c1x+c2x2.
Здесь c0 , c1 и c2 - параметры функции, которые определим с использованием МНК.

В формулу суммы квадратов отклонений подставим аппроксимирующую квадратичную функцию, получим:
Для нахождения минимума функции S приравняем частные производные функции S по параметрам аппроксимирующей функции нулю:

Преобразуем полученные выражения следующим образом:
В результате получаем систему линейных алгебраических уравнений, где в качестве неизвестных выступают параметры квадратичной функции c0 , c1 и c2:

Решаем полученную СЛАУ методом Крамера для систем 3-го порядка и вычисляем параметры c0 , c1 и c2.
Таким образом, мы получаем квадратичную аппроксимирующую функцию:
y*=c0+c1x+c2x2