Содержание
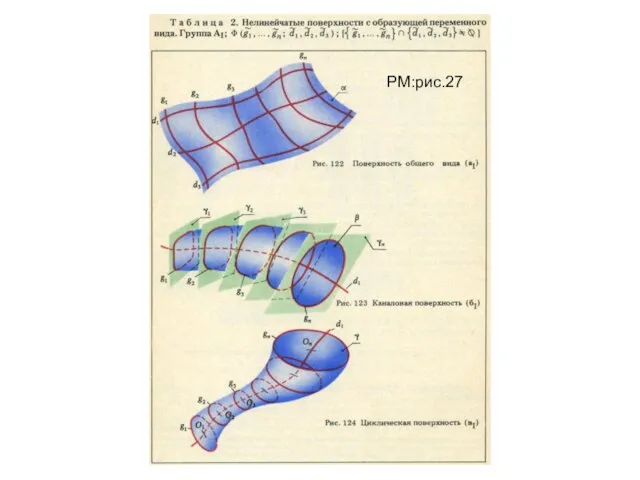
- 2. РМ:рис.27
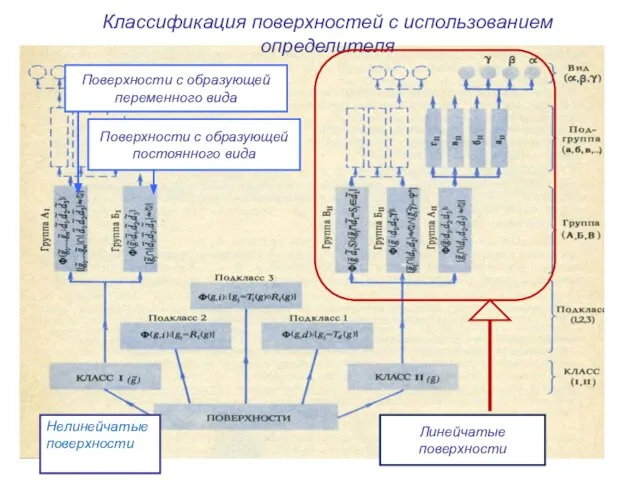
- 4. Классификация поверхностей с использованием определителя Поверхности с образующей переменного вида Поверхности с образующей постоянного вида Нелинейчатые
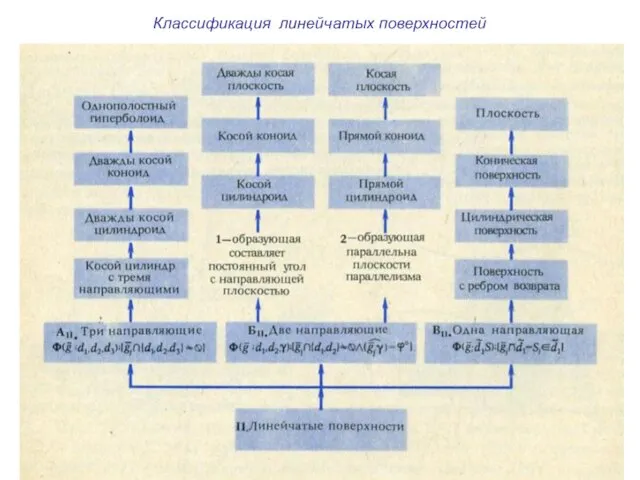
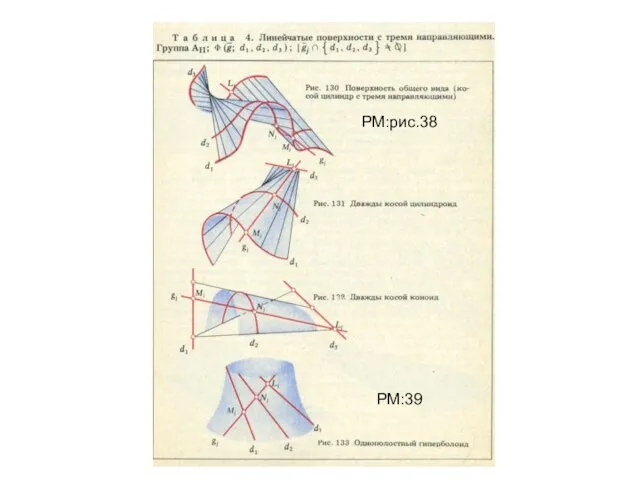
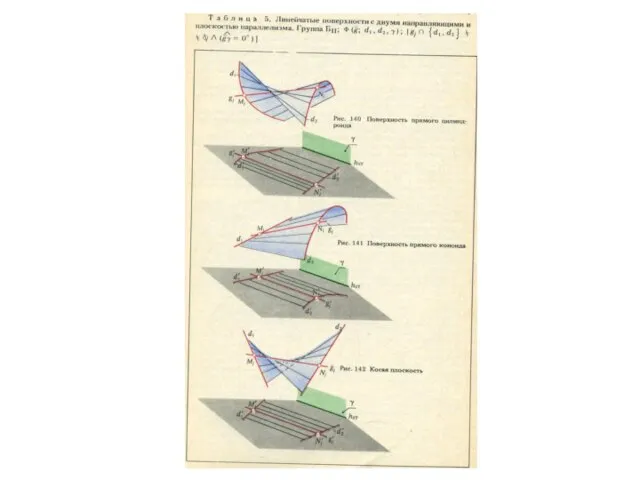
- 5. Классификация линейчатых поверхностей
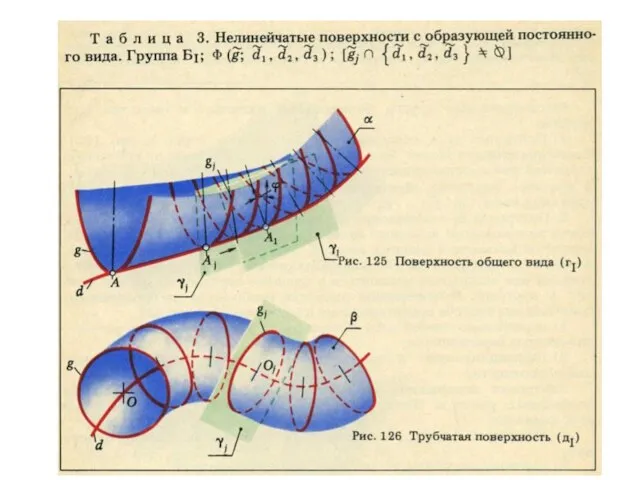
- 6. РМ:рис.38 РМ:39
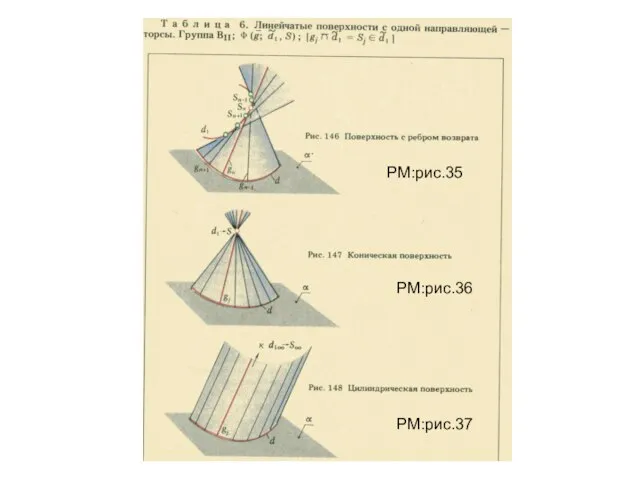
- 8. РМ:рис.35 РМ:рис.36 РМ:рис.37
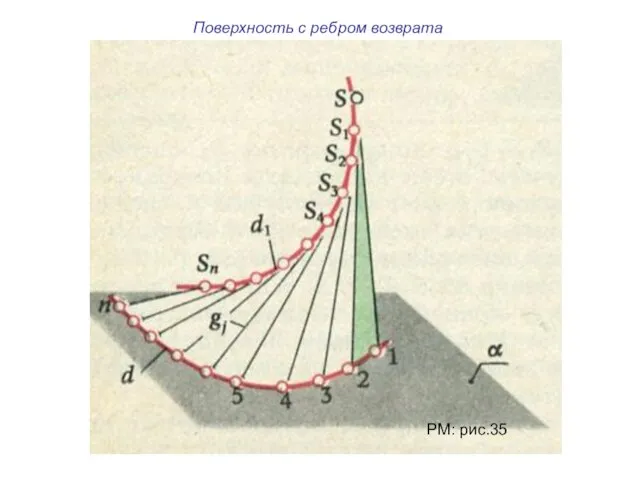
- 9. Поверхность с ребром возврата РМ: рис.35
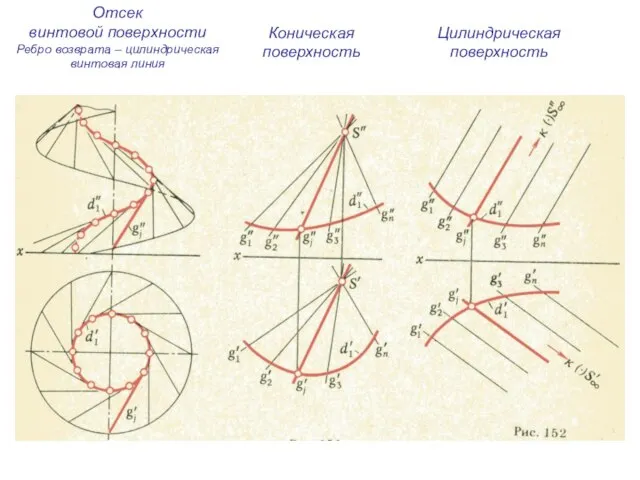
- 10. Отсек винтовой поверхности Ребро возврата – цилиндрическая винтовая линия Коническая поверхность Цилиндрическая поверхность
- 11. Плоскость
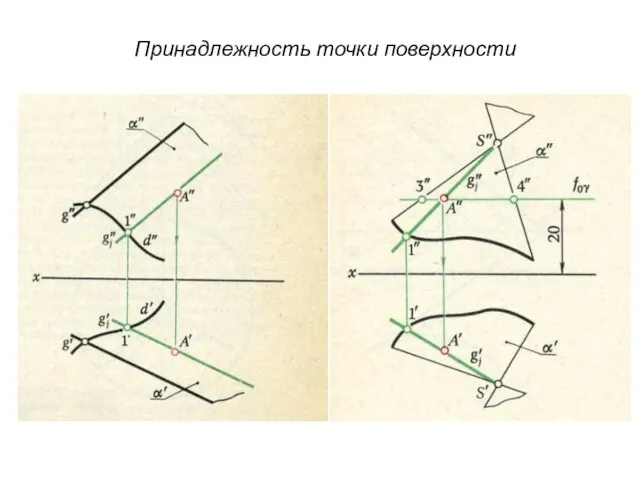
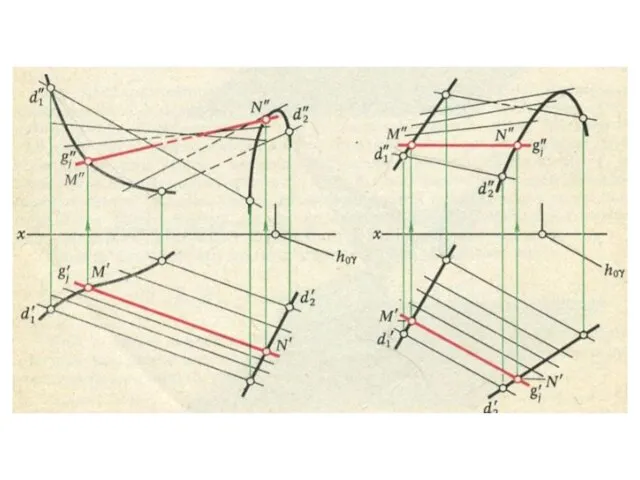
- 12. Принадлежность точки поверхности
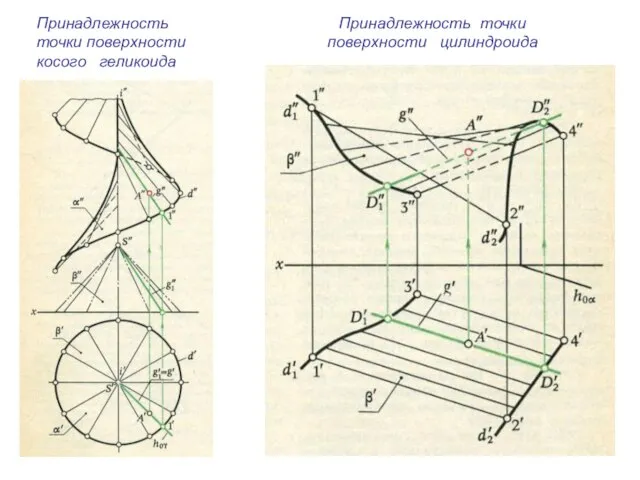
- 13. Принадлежность точки поверхности косого геликоида Принадлежность точки поверхности цилиндроида
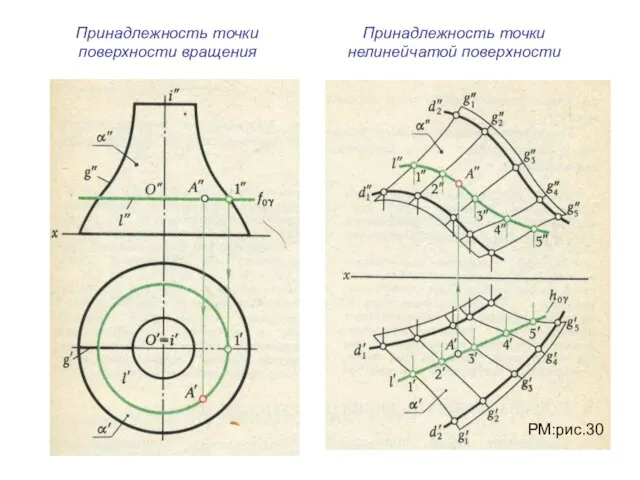
- 14. Принадлежность точки поверхности вращения Принадлежность точки нелинейчатой поверхности РМ:рис.30
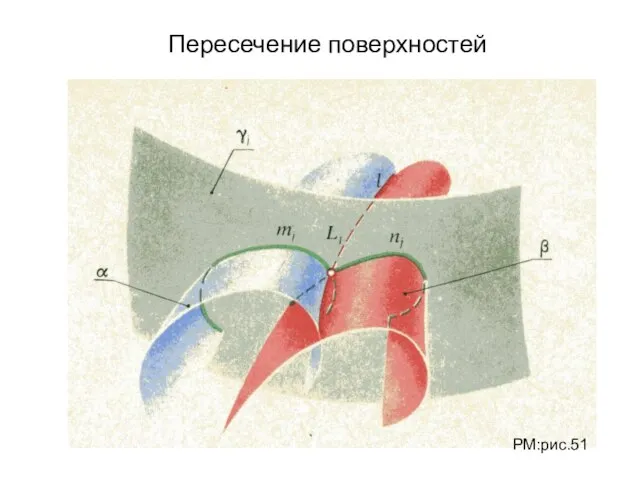
- 16. Пересечение поверхностей РМ:рис.51
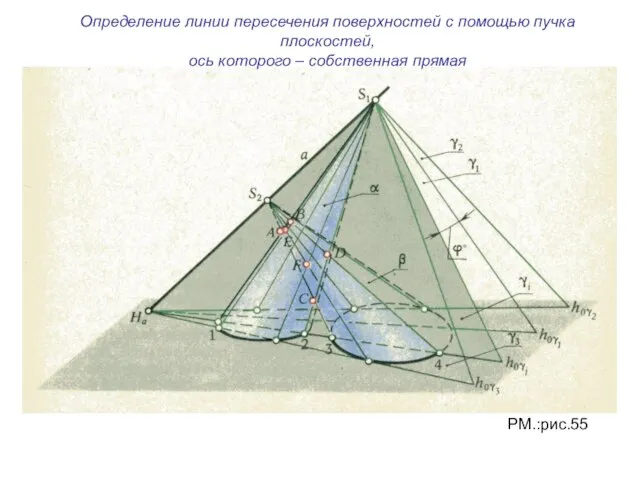
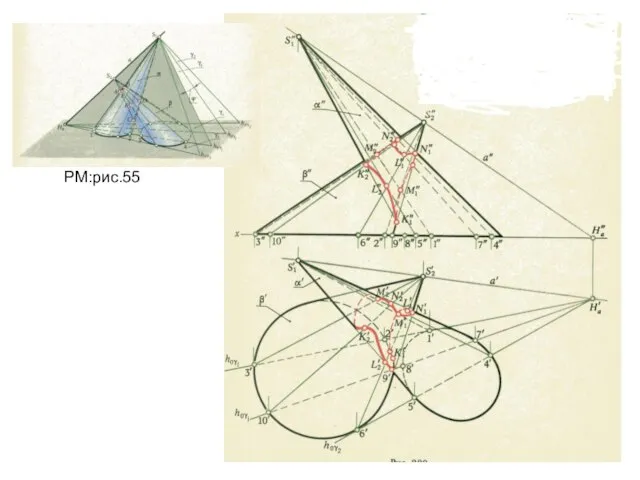
- 17. Определение линии пересечения поверхностей с помощью пучка плоскостей, ось которого – собственная прямая РМ.:рис.55
- 18. РМ:рис.55
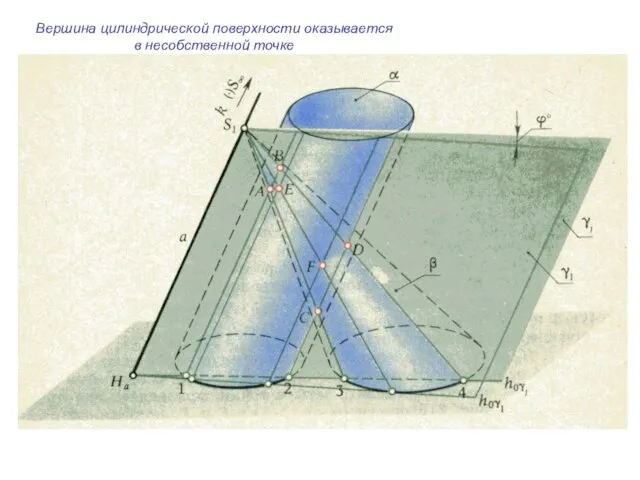
- 19. Вершина цилиндрической поверхности оказывается в несобственной точке
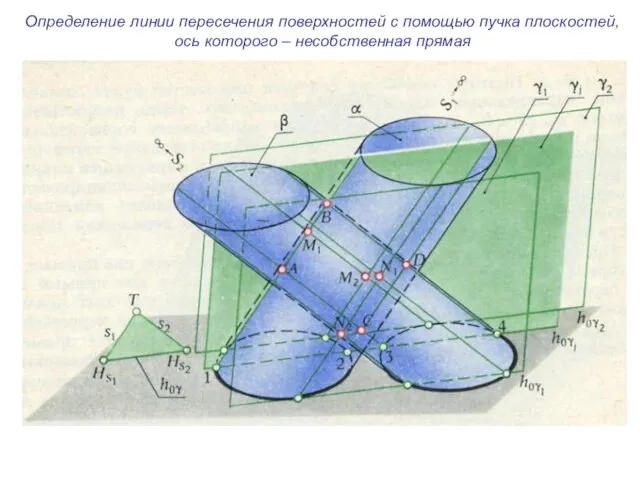
- 20. Определение линии пересечения поверхностей с помощью пучка плоскостей, ось которого – несобственная прямая
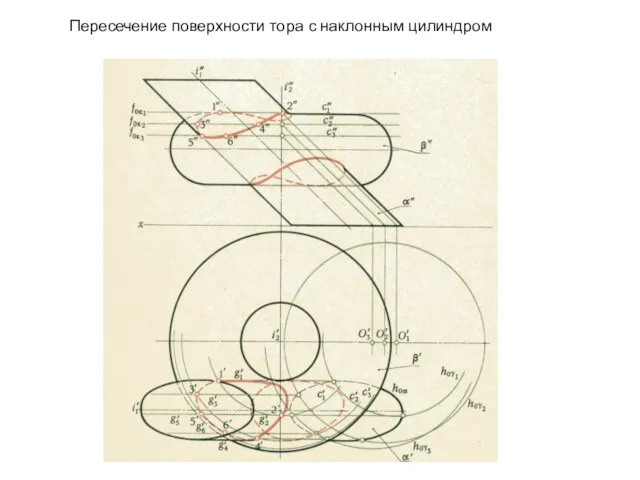
- 22. Пересечение поверхности тора с наклонным цилиндром
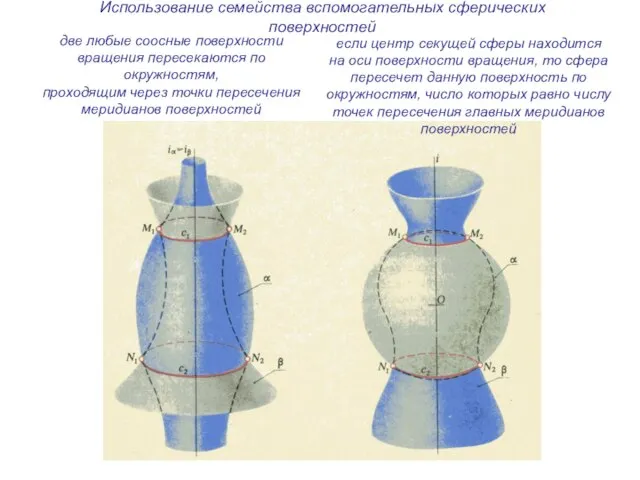
- 23. две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей если центр
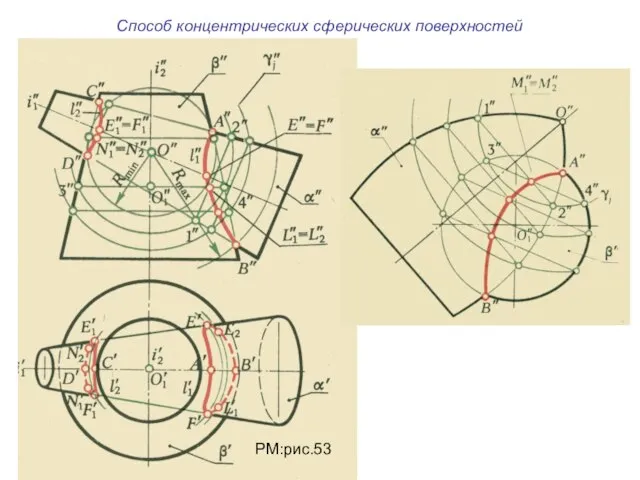
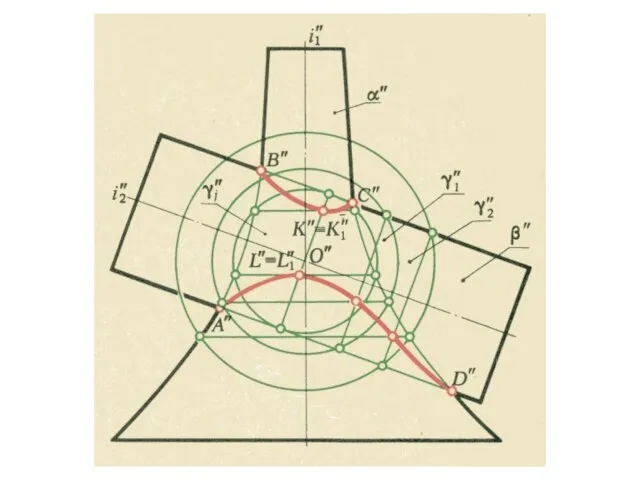
- 24. Способ концентрических сферических поверхностей РМ:рис.53
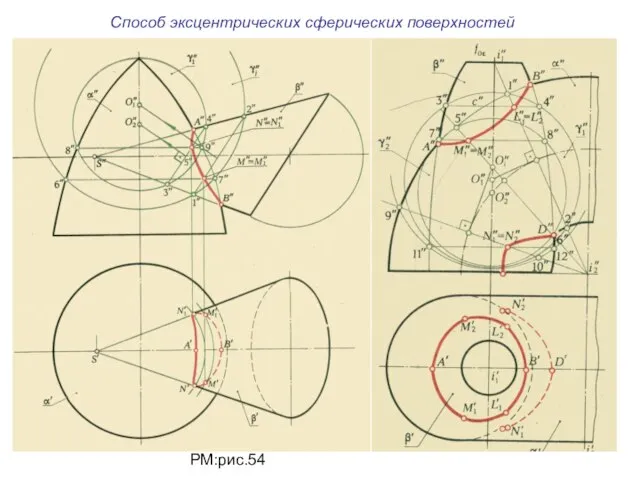
- 26. Способ эксцентрических сферических поверхностей РМ:рис.54
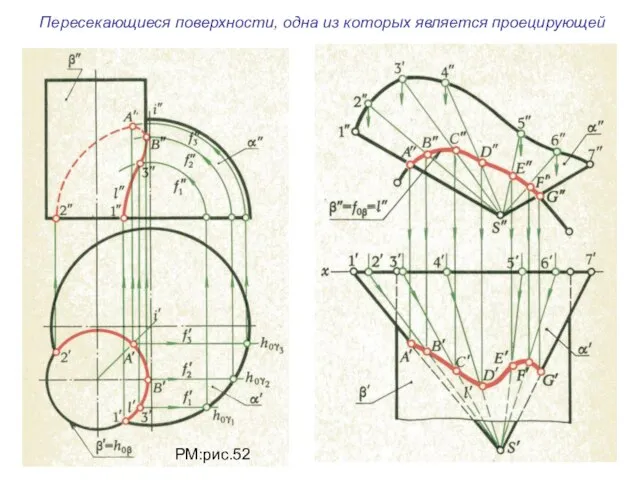
- 27. Пересекающиеся поверхности, одна из которых является проецирующей РМ:рис.52
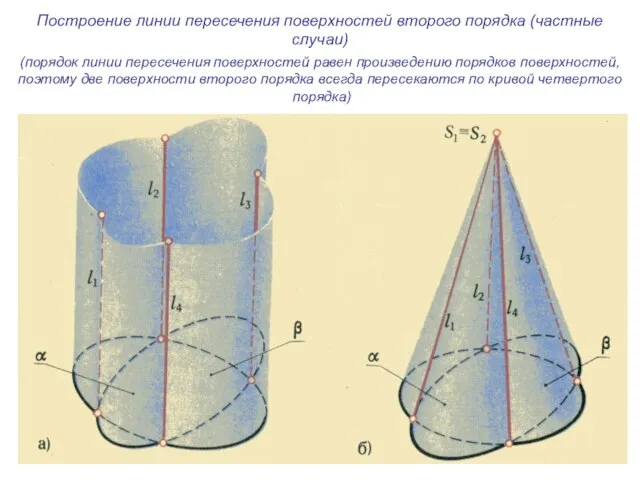
- 28. Построение линии пересечения поверхностей второго порядка (частные случаи) (порядок линии пересечения поверхностей равен произведению порядков поверхностей,
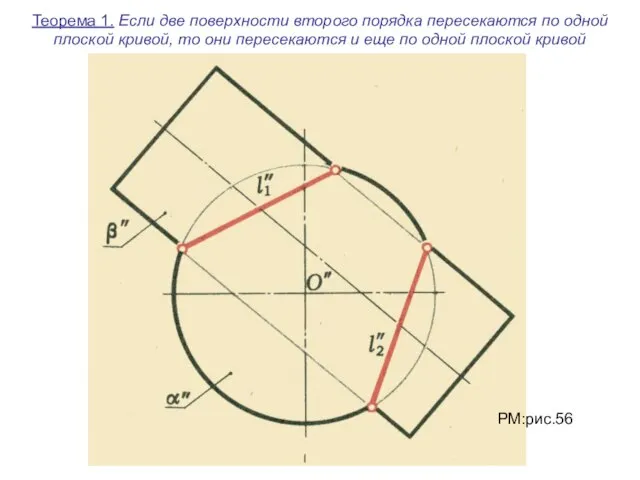
- 29. Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и
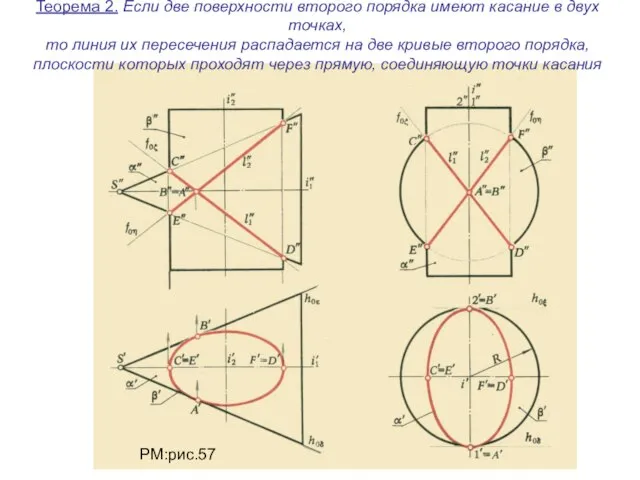
- 30. Теорема 2. Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения
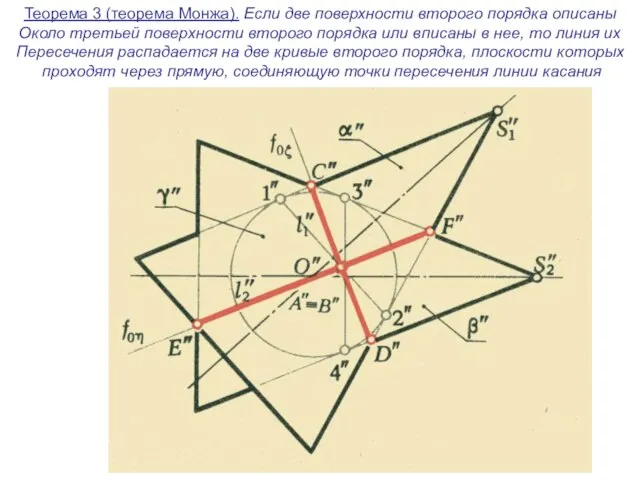
- 31. Теорема 3 (теорема Монжа). Если две поверхности второго порядка описаны Около третьей поверхности второго порядка или
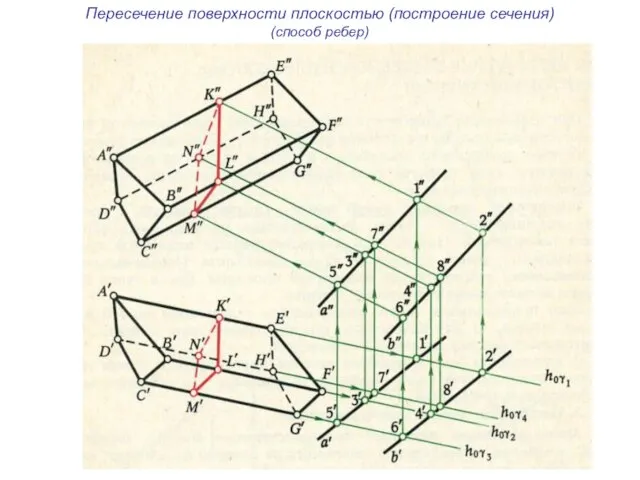
- 32. Пересечение поверхности плоскостью (построение сечения) (способ ребер)
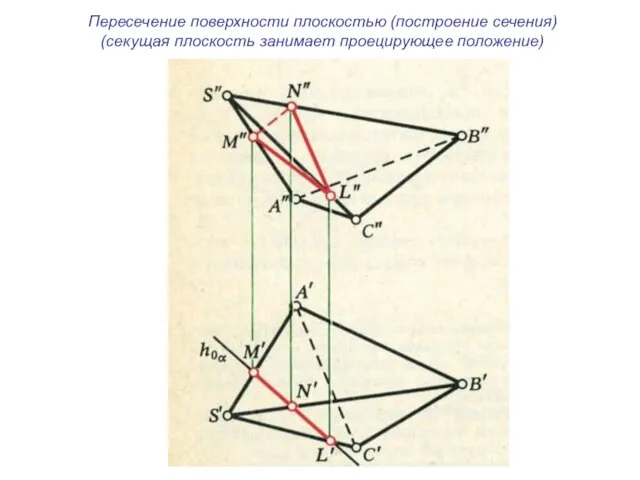
- 33. Пересечение поверхности плоскостью (построение сечения) (секущая плоскость занимает проецирующее положение)
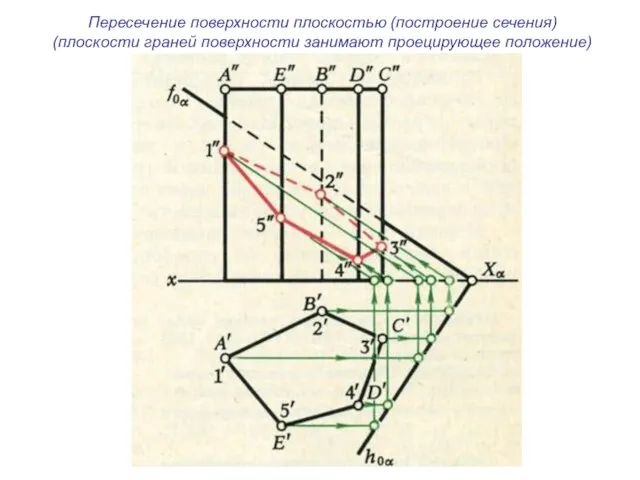
- 34. Пересечение поверхности плоскостью (построение сечения) (плоскости граней поверхности занимают проецирующее положение)
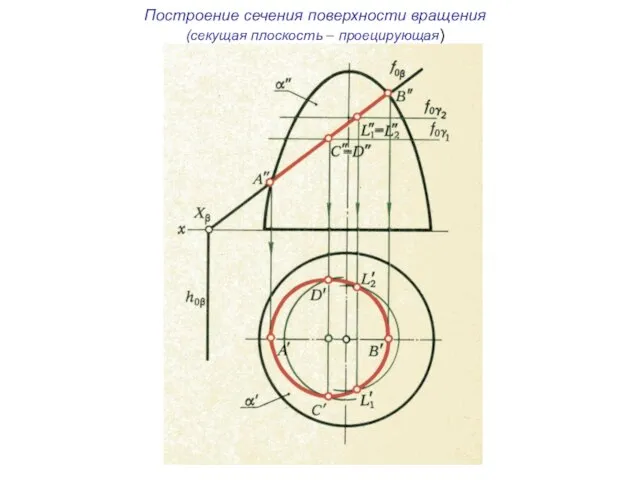
- 35. Построение сечения поверхности вращения (секущая плоскость – проецирующая)
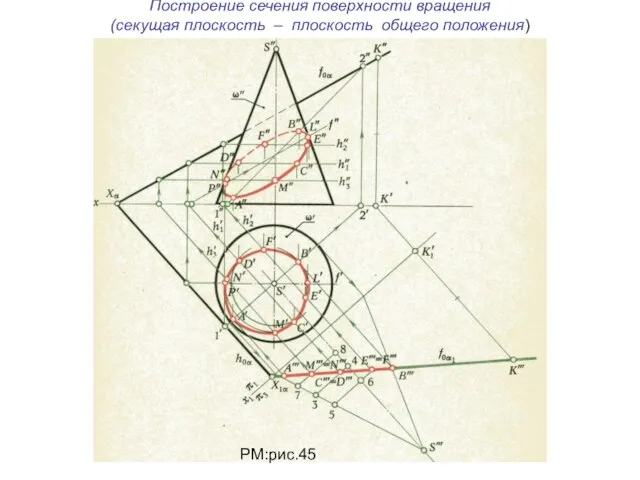
- 36. Построение сечения поверхности вращения (секущая плоскость – плоскость общего положения) РМ:рис.45
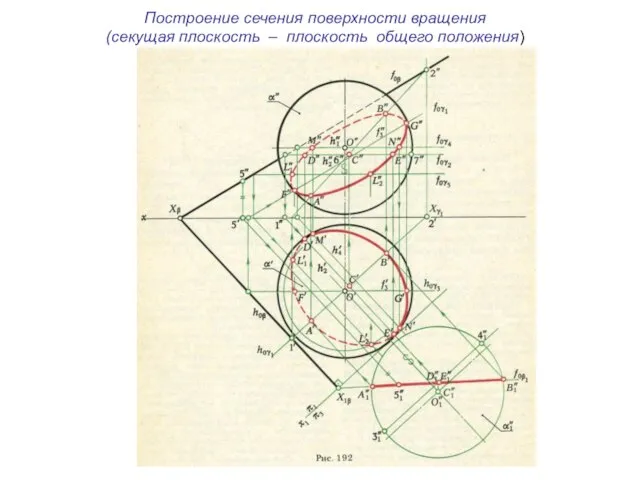
- 37. Построение сечения поверхности вращения (секущая плоскость – плоскость общего положения)
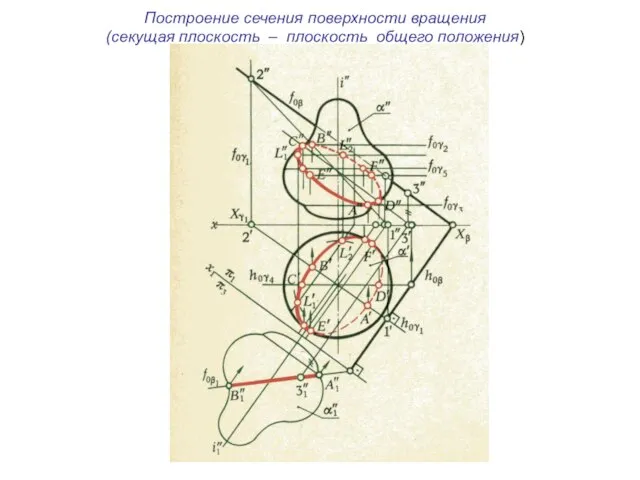
- 38. Построение сечения поверхности вращения (секущая плоскость – плоскость общего положения)
- 40. Скачать презентацию


 Реализация долгосрочных целевых программ:«Профилактика преступлений и иных правонарушений в городе Барнауле на 2010-2012 годы»«Ком
Реализация долгосрочных целевых программ:«Профилактика преступлений и иных правонарушений в городе Барнауле на 2010-2012 годы»«Ком Викторина по стихам Агнии Барто
Викторина по стихам Агнии Барто Календарь
Календарь Проект на тему:«Шапито». Новый танцпол
Проект на тему:«Шапито». Новый танцпол Трансформация формы
Трансформация формы Третий урок
Третий урок Изобретение велосипеда
Изобретение велосипеда Метод персон
Метод персон Геральдика. Герб Англии
Геральдика. Герб Англии Психология вождения
Психология вождения Алгоритм выхода в туристский поход детской группы образовательной организации
Алгоритм выхода в туристский поход детской группы образовательной организации Чистая вода- залог здоровья
Чистая вода- залог здоровья Декоративный натюрморт
Декоративный натюрморт Мастер-класс Рождественский ангел
Мастер-класс Рождественский ангел «Как вдохновлять мужчину, чтобы получать от него подарки, комплименты и цветы»
«Как вдохновлять мужчину, чтобы получать от него подарки, комплименты и цветы» База отдыха Семинская поляна
База отдыха Семинская поляна 1 сентября - День знаний
1 сентября - День знаний Тема урока: Война и её образ в симфонии №7 Дмитрия Дмитриевича Шостаковича.
Тема урока: Война и её образ в симфонии №7 Дмитрия Дмитриевича Шостаковича. Почвы и почвенные ресурсы
Почвы и почвенные ресурсы Экологическая проблема Мы живем в эпоху стремительного прогресса цивилизации. Развитие промышленности, энергетики, а вместе с тем
Экологическая проблема Мы живем в эпоху стремительного прогресса цивилизации. Развитие промышленности, энергетики, а вместе с тем 1.Т2 -1ПЗ
1.Т2 -1ПЗ Рабочее время и отдых
Рабочее время и отдых Три подружки
Три подружки Введение компетентностного подхода в современное образование
Введение компетентностного подхода в современное образование Олимпийские игры
Олимпийские игры История медицины
История медицины  Компетентностный подход в обучении химии
Компетентностный подход в обучении химии Приёмы целеполагания.
Приёмы целеполагания.