Кодирование информации

Кодирование информации
световые;
звуковые;
тепловые;
электрические;
в виде жеста;
в виде движения;
в виде слова и т. д.
Для того чтобы передача информации была успешной, приёмник должен не только получить сигнал, но и расшифровать его. Необходимо заранее договариваться, как понимать те или иные сигналы, т.е. требуется разработка кода.
Сигналы, используемые для передачи информации:

Нотные знаки кодируют музыкальные
произведения:
Правила дорожного движения
кодируются специальными знаками:
Свой код из шести цифр (индекс) имеет
каждый населенный пункт:
Товары маркируются специальными кодами:
Разнообразие используемых нами кодов
Кодирование информации

В середине XIX века французский педагог Луи Брайль придумал специальный способ представления информации для незрячих людей.
Разнообразие используемых нами кодов
Кодирование информации

Одна и та же информация может быть представлена разными кодами.
Существуют три основных способа кодирования информации:
Графический – с помощью рисунков и значков;
Числовой – с помощью чисел;
Символьный – с помощью символов того же
алфавита, что и исходный текст.
Способы кодирования
Кодирование информации

В алфавите любого разговорного языка буквы следуют друг за другом в определенном порядке. Это дает возможность присвоить каждой букве алфавита ее порядковый номер.
Числовое кодирование
Кодирование информации
Например, числовое сообщение
01112001030918
соответствует слову
АЛФАВИТ

Смысл этого способа заключается в том, что символы алфавита (буквы) заменяются символами (буквами) того же алфавита по определенному правилу.
Например, а →б, б → в, в → г и т.д. Тогда слово АЛФАВИТ будет закодировано последовательностью БМХБГЙУ.
Символьное кодирование
Кодирование информации

Это кодирование информации при помощи разнообразных рисунков или значков:
Графическое кодирование
Кодирование информации

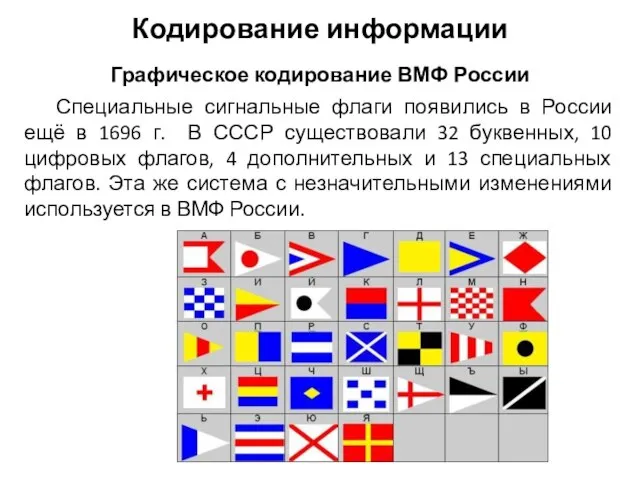
Специальные сигнальные флаги появились в России ещё в 1696 г. В СССР существовали 32 буквенных, 10 цифровых флагов, 4 дополнительных и 13 специальных флагов. Эта же система с незначительными изменениями используется в ВМФ России.
Графическое кодирование ВМФ России
Кодирование информации

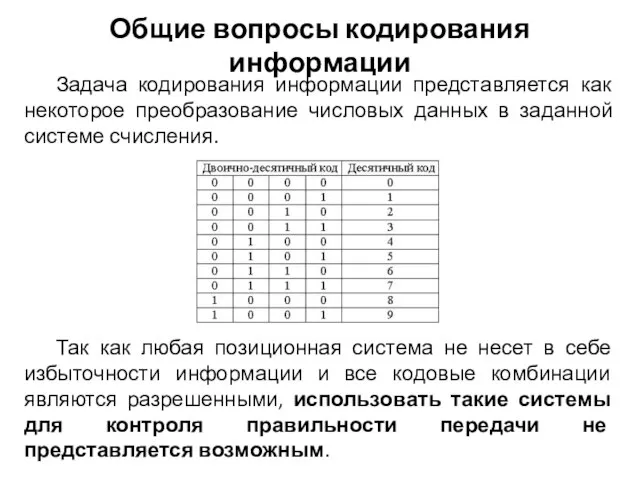
Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления.
Так как любая позиционная система не несет в себе избыточности информации и все кодовые комбинации являются разрешенными, использовать такие системы для контроля правильности передачи не представляется возможным.
Общие вопросы кодирования информации

Систематический код - код, содержащий в себе кроме информационных еще и контрольные разряды.
В контрольные разряды записывается некоторая информация об исходном числе. Поэтому можно говорить, что систематический код обладает избыточностью. При этом абсолютная избыточность будет выражаться количеством контрольных разрядов k, а относительная избыточность - отношением k/n , где n = m + k - общее количество разрядов в кодовом слове (m - количество информационных разрядов).
Общие вопросы кодирования информации
ВАСЯ → 0101 00 1001 00 1011 10 0001 01
ВАСЯ → 0101 00 1001 00 1011 10 0001 01
ВАСЯ → 0101 00 1001 00 1011 10 0001 01
Абсолютная избыточность = 2, относительная избыточность 2/6

Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки. Если имеем n-разрядный код и вероятность искажения одного символа p, то вероятность того, что искажены k символов, а остальные n - k символов не искажены, по теореме умножения вероятностей будет
w = pk(1–p)n-k .
Число кодовых комбинаций, каждая из которых содержит k искаженных элементов, равна числу сочетаний из n по k:
Тогда полная вероятность искажения информации
.
Общие вопросы кодирования информации

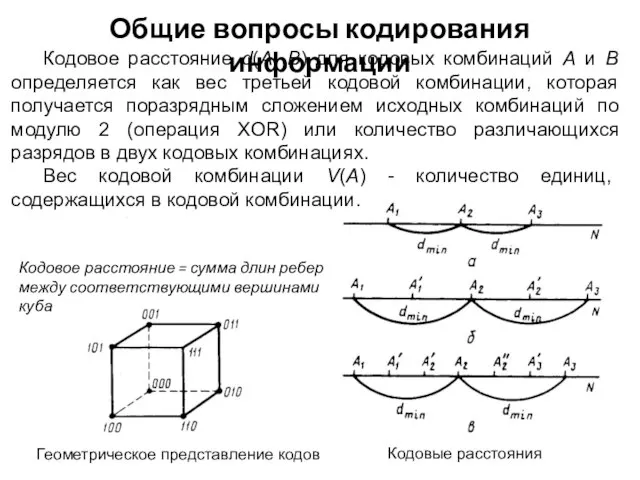
Геометрическое представление кодов
Общие вопросы кодирования информации
Кодовые расстояния
Кодовое расстояние d(A, В) для кодовых комбинаций А и В определяется как вес третьей кодовой комбинации, которая получается поразрядным сложением исходных комбинаций по модулю 2 (операция XOR) или количество различающихся разрядов в двух кодовых комбинациях.
Вес кодовой комбинации V(A) - количество единиц, содержащихся в кодовой комбинации.
Кодовое расстояние = сумма длин ребер между соответствующими вершинами куба

В теории кодирования показано, что систематический код способен обнаружить ошибки только когда минимальное кодовое расстояние для него больше или равно 2t, т.е.
dmin≥2t,
где t - кратность обнаруживаемых ошибок (в случае одиночных ошибок t = 1 и т. д.).
Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодовое слово
В тех случаях, когда необходимо не только обнаружить ошибку, но и исправить ее (т. е. указать место ошибки), минимальное кодовое расстояние должно быть
dmin≥2t+1.
Общие вопросы кодирования информации

Допустим, имеем следующий набор кодовых комбинаций:
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Геометрическая модель этого кода – куб. Для рассматриваемого кода dmin= 1. Учитывая, что рассматриваемый код по построению является неизбыточным, можно утверждать, что любой неизбыточный код имеет dmin= 1 и наоборот, если dmin= 1, код является неизбыточным.
Общие вопросы кодирования информации

Для построения простейшего избыточного кода, который может обнаруживать одну ошибку, нужно отобрать рабочие комбинации на расстоянии d(A, B) ≥ 2.
В рассматриваемом коде можно выбрать следующие комбинации:
0 1 0
1 0 0
1 1 1
0 0 1
где Mр – число разрешенных (или рабочих) комбинаций.
Избыточность полученного кода
R=k/n=(n-m)/n=1/3≈33%.
Общие вопросы кодирования информации
Мр = 4

Если требуется обнаруживать две ошибки, то рабочих комбинаций будет только две, например
0 0 0
1 1 1
0 1 0
1 0 1
минимальное кодовое расстояние в этом случае dmin = 3, избыточность
R=k/n=(n-m)/n=2/3≈67%.
Если требуется обнаруживать три ошибки, dmin ≥ 4, что невозможно обеспечить в рассматриваемом коде, так как кодовое расстояние d(A, B) ≤ 3.
Общие вопросы кодирования информации
Мр = 2
Мр = 2

Общие вопросы кодирования информации
Возможны несколько стратегий борьбы с ошибками:
обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков (компьютерные сети)
обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков (потоковые мультимедиа-системы)
исправление ошибок

Эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.
Общие вопросы кодирования информации

Код строится следующим образом: буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним - 0. Каждая из полученных групп, в свою очередь, разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.
Методика кодирования Шеннона-Фано
Эффективное кодирование информации

Множество вероятностей в предыдущей таблице можно было разбить иным образом:
Методика кодирования Шеннона-Фано
Эффективное кодирование информации
Предыдущий вариант

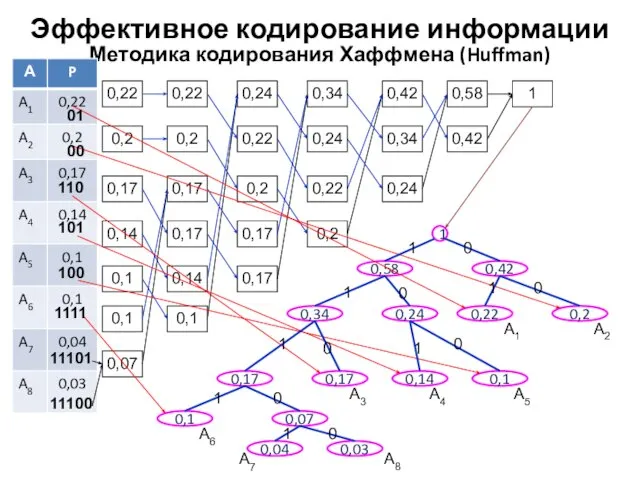
Методика кодирования Хаффмена (Huffman)
Эффективное кодирование информации
0,22
0,2
0,17
0,14
0,1
0,1
0,07
0,22
0,2
0,17
0,17
0,14
0,1
0,24
0,22
0,2
0,17
0,17
0,34
0,24
0,22
0,2
0,42
0,34
0,24
0,58
0,42
1
1
0,58
0,42
0,34
0,24
0,22
0,2
0,1
0,14
0,17
0,17
0,1
0,07
0,03
0,04
А1
А2
А3
А4
А5
А6
А7
А8
1
0
0
0
0
0
0
1
0
1
1
1
1
1
11100
01
00
110
101
100
1111
11101

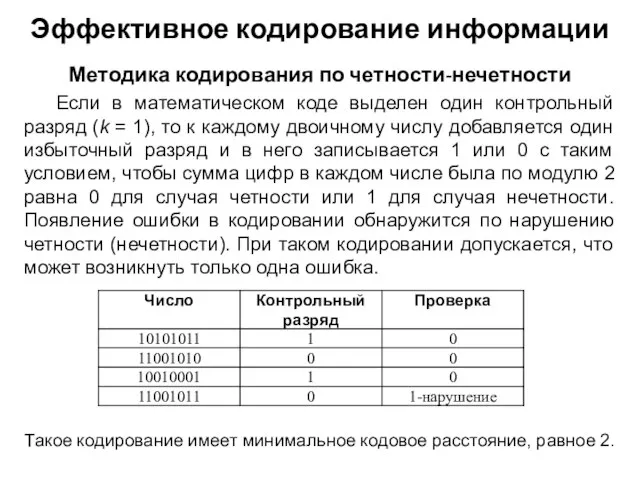
Если в математическом коде выделен один контрольный разряд (k = 1), то к каждому двоичному числу добавляется один избыточный разряд и в него записывается 1 или 0 с таким условием, чтобы сумма цифр в каждом числе была по модулю 2 равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнаружится по нарушению четности (нечетности). При таком кодировании допускается, что может возникнуть только одна ошибка.
Такое кодирование имеет минимальное кодовое расстояние, равное 2.
Методика кодирования по четности-нечетности
Эффективное кодирование информации

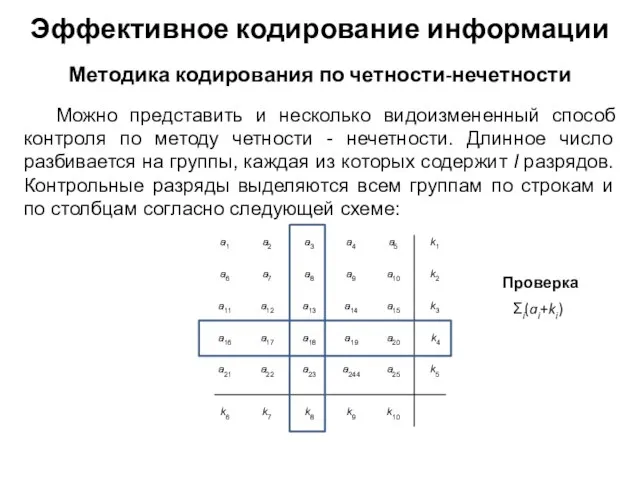
Можно представить и несколько видоизмененный способ контроля по методу четности - нечетности. Длинное число разбивается на группы, каждая из которых содержит l разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно следующей схеме:
Методика кодирования по четности-нечетности
Эффективное кодирование информации
Σi(ai+ki)
Проверка

Методика кодирования Хэмминга
Эффективное кодирование информации
Предположим, что имеется код, содержащий m информационных разрядов и k контрольных разрядов. Запись на k позиций определяется при проверке на четность каждой из проверяемых k групп информационных символов. Пусть было проведено k проверок. Если результат проверки свидетельствует об отсутствии ошибки, то запишем 0, если есть ошибка, то запишем 1 . Запись полученной последовательности символов образует двоичное, контрольное число, указывающее номер позиции, где произошла ошибка. При отсутствии ошибки в данной позиции последовательность будет содержать только нули. Полученное таким образом число описывает n = (m + k + 1) событий. Следовательно, справедливо неравенство
2k ≥ (m + k + 1).
Пример кода: 1001011001 0100 2k ≥ (m + k + 1) ⇒ 16 ≥ 15
m k

Методика кодирования Хэмминга
Эффективное кодирование информации
Определить максимальное значение m для данного k можно из следующего:
n… 1 2 3 4… 8…15 16…31 32…63 64
m…0 0 1 1… 4…11 11…26 26…57 57
k… 1 2 2 3… 4…4 5…5 6…6 7
Полученное таким образом число описывает n = (m + k + 1) событий. Следовательно, справедливо неравенство
2k ≥ (m + k + 1).
Пример кода: 1001011001 0100 2k ≥ (m + k + 1) ⇒ 16 ≥ 15
m k

Методика кодирования Хэмминга
Эффективное кодирование информации
Определим теперь позиции, которые надлежит проверить в каждой из k проверок. Если в кодовой комбинации ошибок нет, то контрольное число содержит только нули. Если в первом разряде контрольного числа стоит 1, то, значит, в результате первой проверки обнаружена ошибка. Имея таблицу двоичных эквивалентов для десятичных чисел, можно сказать, что, например, первая проверка охватывает позиции 1, 3, 5, 7, 9 и т. д., вторая проверка — позиции 2, 3, 6, 7, 10.
Проверка Проверяемые разряды
1... 1,3,5,7,9,11,13,15...
2... 2,3,6,7, 10, 11, 14, 15, 18, 19,22,23...
3... 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23...
4... 8,9,10,11,12,13,14,15,24...

Методика кодирования Хэмминга
Эффективное кодирование информации
Кодирование информации по методу Хэмминга для 7-миразрядного кода
n=7, m=4, k=3 и контрольными будут разряды 1, 2, 4
Проверка Проверяемые
разряды
1... 1,3,5,7,9...
2... 2,3,6,7, 10...
3... 4, 5, 6, 7, 12...
4... 8,9,10,11...
0
0
0
1
1
0
1
2=510
.

Обычно выделяют два класса алгоритмов сжатия
Алгоритмы сжатия информации
Эффективное кодирование информации
Сжатие без потерь
Сжатие с потерями