Содержание
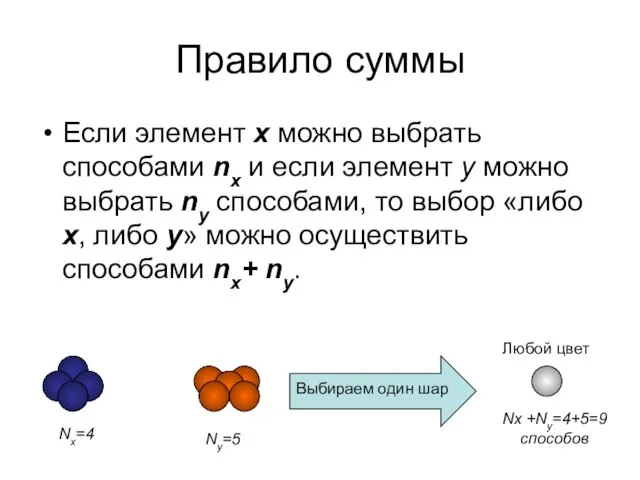
- 2. Правило суммы Если элемент x можно выбрать способами nx и если элемент y можно выбрать ny
- 3. Правило суммы Правило суммы используется тогда, когда варианты соединяются словом «ИЛИ»
- 4. Пример 1 Сколько различных символов можно закодировать, используя код Морзе длиной не менее 5 и (или)
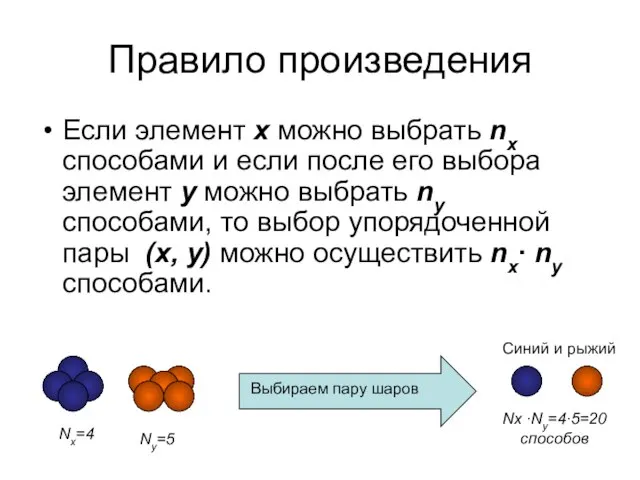
- 5. Правило произведения Если элемент x можно выбрать nx способами и если после его выбора элемент y
- 6. Пример 2. Номер автомобиля состоит из шести мест, на первом – буква, затем – три цифры,
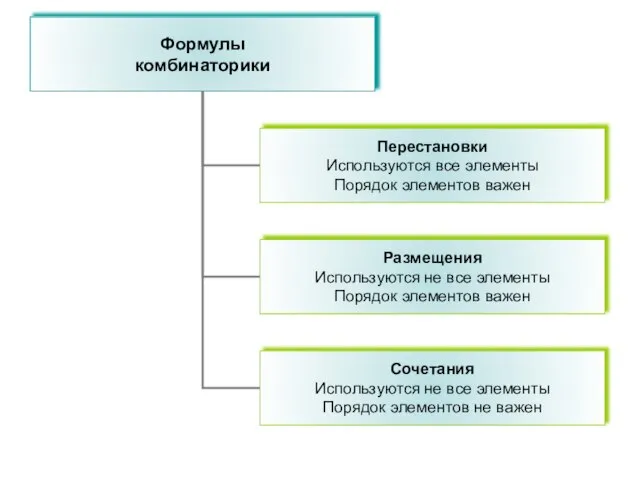
- 7. Формулы комбинаторики Перестановки Размещения Сочетания
- 8. Два главных вопроса В задаче требуется переставить все элементы или требуется выбрать несколько из них? (все
- 9. Перестановки Используются все элементы Порядок элементов важен
- 10. Перестановки без повторений Перестановками без повторений из n различных элементов называются все возможные последовательности этих n
- 11. Перестановки без повторений 6 различных перестановок
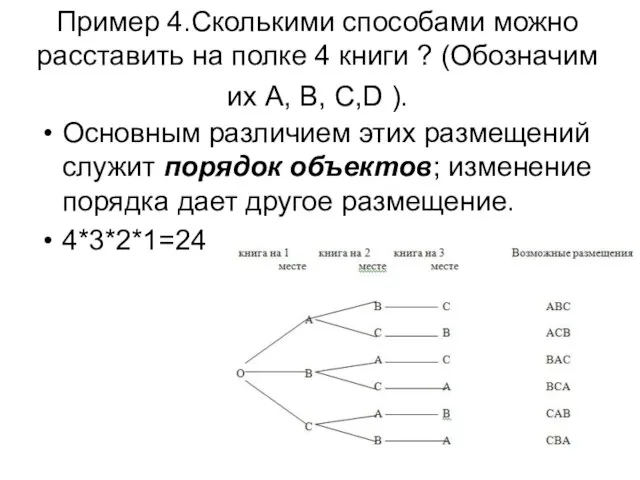
- 12. Пример 4.Сколькими способами можно расставить на полке 4 книги ? (Обозначим их А, В, С,D ).
- 13. Пример 5 По следствию должны пройти пять человек: A, B, C, D, E. Cколько вариантов того,
- 14. Решение АВ??? - таких вариантов Р3=3!=6 ?АВ?? ??АВ? ???АВ Всего вариантов М=6*4=24
- 15. Перестановки с повторениями Перестановки с повторением из n элементов k типов число элементов 1-го типа n1;
- 16. Перестановки с повторениями n1=2 n2=1 n=n1+n2=2+1=3 3 различные перестановки
- 17. Пример 6. Сколько чисел можно создать из двух цифр «2» и двух цифр «1»? 1122 1212
- 18. Пример 7. Существует конечное число неэквивалентных друг другу логических функций, зависящих от трех аргументов. Среди них
- 19. Решение 8!/(2!*6!)=23
- 20. Размещения (выборки) Используются не все элементы Порядок элементов важен
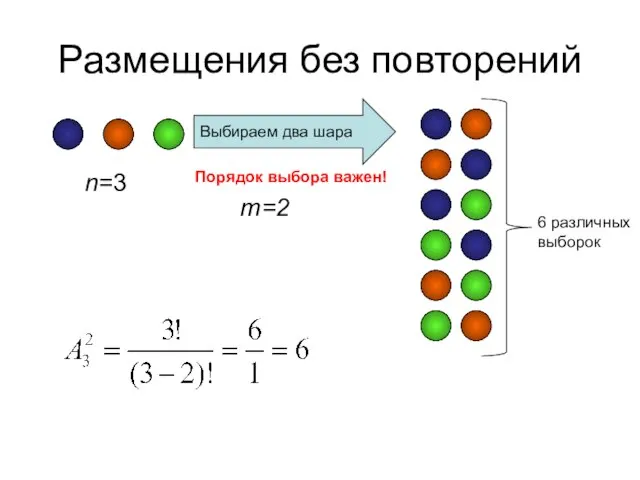
- 21. Размещения без повторений Размещениями без повторений из n различных элементов по m элементов называются все такие
- 22. Размещения без повторений n=3 Выбираем два шара m=2 Порядок выбора важен! 6 различных выборок
- 23. Пример 8 В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами
- 24. Решение Всего вариантов - выбрать три из восьми без повторения, т.к. один и тот же не
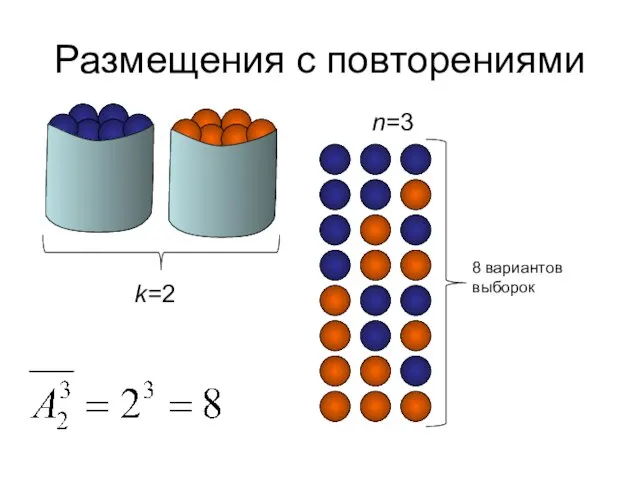
- 25. Размещения с повторениями Размещения с повторениями из элементов k типов по m элементов (k и m
- 26. Размещения с повторениями k=2 n=3 8 вариантов выборок
- 27. Пример 9 Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; на
- 28. Решение 1) Всего вариантов 2) Всего вариантов 3) Всего вариантов N=10*9*9*9
- 29. Сочетания Используются не все элементы Порядок элементов не важен
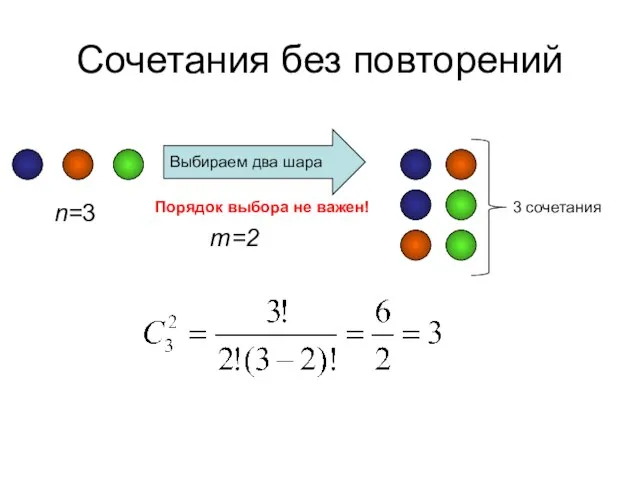
- 30. Сочетания без повторений Сочетаниями без повторений из n различных элементов по m элементов называются все такие
- 31. Сочетания без повторений n=3 Выбираем два шара m=2 Порядок выбора не важен! 3 сочетания
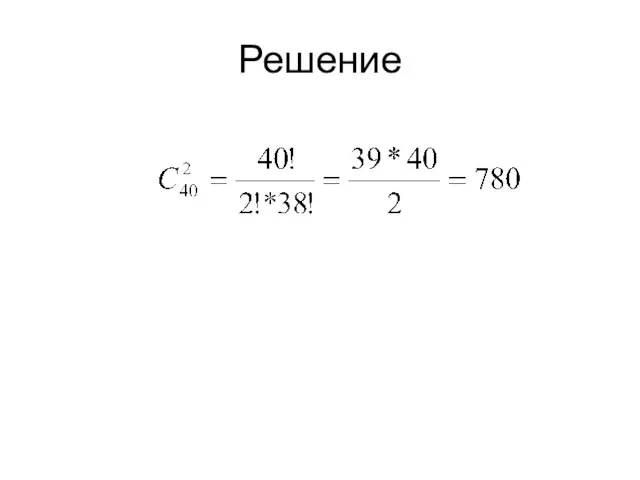
- 32. Пример 10 В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии.
- 33. Решение
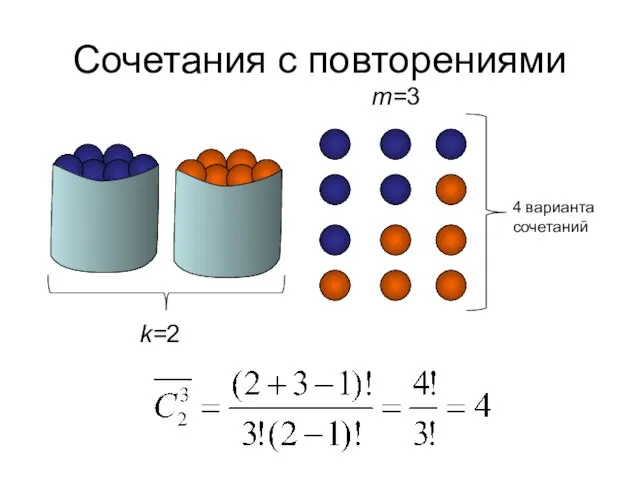
- 34. Сочетания с повторениями Сочетаниями с повторениями из элементов k типов по m элементов (m и k
- 35. Сочетания с повторениями k=2 m=3 4 варианта сочетаний
- 36. Пример 11 Имеется 2 типа цветов, количество цветов не ограничено. Сколько различных букетов можно составить из
- 37. Пример 12 Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из
- 38. Решение Сочетание с повторением: (5+3-1)!/(3!*(5-1) !)=35
- 40. Пример 13. Сколькими способами можно выбрать четырех студентов, которые будут получать стипендию, из восьми. Решение. Мы
- 41. Пример 14. Паша, Сережа, Андрей и Антон думают надеть ли на торжественный вечер галстуки или бабочки.
- 42. Задача1 Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено»,
- 43. Задача 2 Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность
- 44. Задача 3 Вася и Петя передают друг другу сообщения, используя синий, красный и зеленый фонарики. Это
- 45. Задача 4 Для кодирования 300 различных сообщений используются 5 последовательных цветовых вспышек. Вспышки одинаковой длительности, для
- 46. Задача 5 Сколько существует четырехзначных чисел, в записи которых все цифры различны?
- 47. Задача 6 Виктор хочет купить пять разных книг, но денег у него хватает только на три
- 49. Скачать презентацию





































 Н. М. Карамзин и Симбирск
Н. М. Карамзин и Симбирск Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155
Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155 [Название]
[Название] Презентация на тему Образование в Японии
Презентация на тему Образование в Японии Междисциплинарная интеграция с использованием информационных технологий.
Междисциплинарная интеграция с использованием информационных технологий. МИФ или РЕАЛЬНОСТЬ?
МИФ или РЕАЛЬНОСТЬ? Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п
Исследователь и творец: какой он? ( 3 Межрегиональная конференция «Организация исследовательской деятельности детей и молодёжи: п Турция
Турция Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли
Нас ждет глобальное потепление! Льды растают и затопят низменные участки земли Сказки М.Е. Салтыкова-Щедрина.
Сказки М.Е. Салтыкова-Щедрина. Умножение на 4
Умножение на 4 Загадка смерти Александра I
Загадка смерти Александра I Тушь Extreme Fashion
Тушь Extreme Fashion МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов
МАСТЕР-КЛАСС Критериально-ориентированное педагогическое тестирование Модуль № 2. Внутренняя экспертизатестов Australian financial services consulting company (fintech)
Australian financial services consulting company (fintech) Афиши к спектаклю по драме А. Островского Гроза
Афиши к спектаклю по драме А. Островского Гроза Мастер - класс по нетрадиционным техникам рисования
Мастер - класс по нетрадиционным техникам рисования 1 сентября – День знаний
1 сентября – День знаний Физика и искусство
Физика и искусство Автомобильная промышленность
Автомобильная промышленность Арт менеджмент
Арт менеджмент  Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона
Бакалаврская работа. Анализ проектного финансирования как средства стимулирования экономического роста региона Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ
Диагностика электоральной ситуации перед выборами в Государственную Думу РФПо заказу РЦОИТ при ЦИК РФ РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА
РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА о картофеле
о картофеле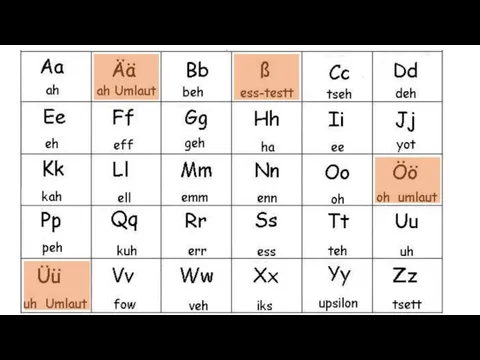 алфавит + звуки
алфавит + звуки Нарезание резьбы
Нарезание резьбы INFECTION CONTROL IN ICU
INFECTION CONTROL IN ICU