Контрольная карта шухарта

Контрольна карта — це графічний засіб застосовування статистичних методів, важливість яких для керування виробничими процесами була вперше показана доктором Уолтером Шухартом у 1924 р.
Теорія контрольних карт розрізняє два види мінливості.
Перший вид — випадкова мінливість через «випадкові причини» (відомі ще як «звичайні причини»). Вона зумовлена широким набором причин, що присутні постійно, які нелегко виявити, кожна з таких причин становить дуже малу частку загальної мінливості, і жодна з них не значима сама по собі. Проте сума всіх цих причин вимірна і вважають, що вона є внутрішньою суттю процесу. Унеможливлення чи зменшення впливу звичайних причин вимагає управлінських рішень для виділення ресурсів на поліпшення процесу і системи.

Наведемо приклади групи факторів випадкового характеру:
• випадкові розкид характеристик матеріалів, напівфабрикатів і комплектуючих виробів;
• випадкові розкид параметрів технологічних процесів випадкові розкид параметрів технологічних процесів (навколишнє середовище і робоче тіло);
• випадкові розкид параметрів технологічних процесів випадкові розкид параметрів технологічних процесів (навколишнє середовище і робоче тіло);
• випадкові розкид характеристик і параметрів засобів технологічного оснащення, вимірювальних приладів, ріжучого і вимірювального інструменту, стендового випробувального устаткування тощо;
• випадкові несприятливі поєднання допусків в розмірних технологічних ланцюжках при виготовленні продукції і т.д.

Мінливість, обумовлена факторами випадкового характеру, може бути зменшена шляхом проведення відповідних організаційно-технічних заходів на основі дослідження результатів їх статистичного аналізу та опису їх прояви статистичними закономірностями.
Другий вид мінливості являє собою реальні зміни в процесі. Вони можуть бути наслідком деяких обумовлених причин, не властивих процесу внутрішньо і можуть бути усунуті, принаймні теоретично. Ці причини, які виявляють, розглядають як «невипадкові» чи «особливі» причини зміни. До них можуть бути віднесені недостатня однорідність матеріалу, поломка інструменту, кваліфікація персоналу, невиконання процедур, низька ефективність виробничого чи контрольного устатковання.

Особливі причини мінливості є невипадкові фактори, що порушують стабільний перебіг процесу. Наведемо приклади групи факторів невипадкового характеру:
• застосування матеріалів, напівфабрикатів і комплектуючих виробів, не передбачених технологічними процесами, в тому числі з простроченими термінами придатності;
• недотримання встановлених нормативно-технічною документацією прийомів, методів і режимів обробки виробів і їх випробувань;
• використання не атестованих під час засобів контролю та засобів технологічного оснащення з простроченими термінами придатності;
• незадовільний стан засобів технологічного оснащення, ремонтної бази, лабораторного обладнання і т.д.;
• відсутність закріплення конкретних видів робіт (операцій) за певними виконавцями;
• неповне завершення попередніх операцій.

Мета контрольних карт — знайти неприродні зміни в даних для процесів, які повторюються, і дати критерії для виявлення недостатку статистичного керування. Процес знаходиться в статистично керованому стані, якщо мінливість викликана тільки випадковими причинами. Після визначення цього прийнятного рівня мінливості будь-який відхил від нього вважають результатом дії особливих причин, які варто виявити, вилучити чи послабити.
Задача статистичного керування процесами — забезпечення і підтримка процесів на прийнятному і стабільному рівні, що гарантує відповідність продукції і послуг встановленим вимогам. Головний статистичний інструмент, який використовують для цього, — контрольна карта — графічний засіб представлення і зіставлення інформації, що базується на послідовності вибірок, що віддзеркалюють поточний стан процесу, із межами, встановленими на основі мінливості, яка внутрішньо властива процесу.

Метод контрольних карт допомагає визначити, чи дійсно процес досяг статистично керованого стану на правильно заданому рівні або залишається в цьому стані, а потім підтримувати керування і високий ступінь однорідності найважливіших характеристик продукції або послуги за допомогою неперервного фіксування інформації про якість продукції в процесі виробництва. Використовування контрольної карти і її ретельний аналіз ведуть до кращого розуміння й удосконалення процесу.

Для карти Шухарта потрібні вибіркові дані процесу, одержані через приблизно рівні інтервали. Інтервали можуть бути задані або за часом (наприклад погодинно), або за кількістю продукції (кожна партія).
Як правило, кожна підгрупа складається з однотипних одиниць продукції чи послуг з тими самими контрольованими показниками і всі підгрупи мають рівний обсяг.
Для кожної підгрупи визначають одну чи кілька характеристик, таких як середнє арифметичне підгрупи та розмах підгрупи R або вибіркове стандартне відхилення s.

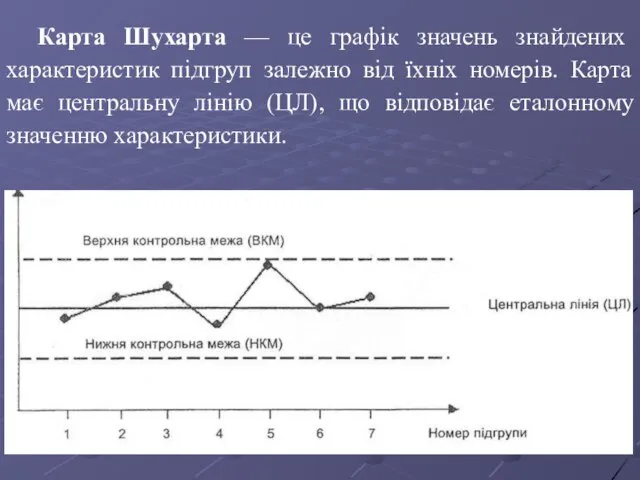
Карта Шухарта — це графік значень знайдених характеристик підгруп залежно від їхніх номерів. Карта має центральну лінію (ЦЛ), що відповідає еталонному значенню характеристики.

Під час оцінювання того, чи знаходиться процес у статистично керованому стані, еталонним звичайно служить середнє арифметичне розглянутих даних.
Під час керування еталонним процесом служить довгострокове значення характеристики, встановлене в технічних умовах, чи її номінальне значення, що базується на попередній інформації про процес, або намічене цільове значення характеристики продукції чи послуги.
Карта Шухарта має дві контрольні межі (які визначають статистично) щодо центральної лінії, які називають верхньою контрольною межею (ВКМ) і нижньою контрольною межею (НКМ) (див. рисунок 1).

Контрольні межі на карті Шухарта містяться на відстані 3σ від центральної лінії, де σ — генеральне стандартне відхилення.
Мінливість усередині підгрупи є мірою випадкових варіацій.
Для одержання оцінки σ обчислюють вибіркове стандартне відхилення чи множать вибірковий розмах на відповідний коефіцієнт. Ця міра не охоплює варіації між групами, а тільки між елементами всередині підгрупи.

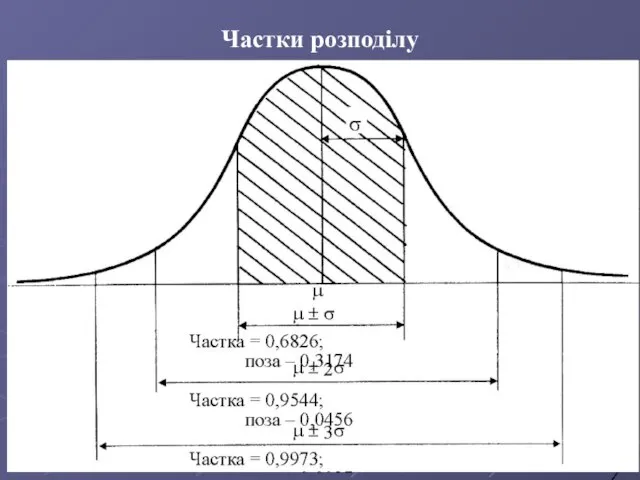
Межі 3σ вказують, що приблизно 99,7 % значень характеристики підгруп потраплять у ці межі за умови, що процес знаходиться в статистично керованому стані. Іншими словами, є ризик, рівний приблизно 0,3 % чи в середньому три на тисячу випадків, що нанесена точка виявиться поза контрольними межами, коли процес знаходиться в статистично керованому стані.
Вживають слово «приблизно», оскільки відхилення від вихідних припущень, таких як вид розподілу даних, будуть впливати на значення імовірності.
Треба відзначити, що деякі спеціалісти віддають перевагу множнику 3,09 замість множника 3, щоб забезпечити номінальне значення імовірності 0,2 % (у середньому два спостереження, що вводять в оману, на тисячу), але Шухарт вибрав число 3, щоб не давати підстав до розгляду точних ймовірностей.

Аналогічно деякі спеціалісти застосовують фактичні значення ймовірностей для карт, що базуються на розподілах, відмінних від нормального, таких як карти розмахів і часток невідповідностей. І в цьому випадку в карті Шухарта також використовують межі на відстані ±3σ замість імовірнісних меж, спрощуючи емпіричну інтерпретацію.
Імовірність того, що порушення меж справді випадкова подія, а не реальний сигнал, вважають настільки малою, що з появою точки поза межами треба вжити певних заходів. Оскільки заходи треба приймати саме на цьому етапі, то контрольні межі 3σ іноді називають «межі дій».
Часто на контрольній карті межі проводять ще і на відстані 2σ. Тоді будь-яке вибіркове значення, що попадає за межі 2σ, може служити застереженням про можливість виходу процесу зі ста­ну статистичної керованості. Тому межі 2σ іноді називають «попереджувальні».

Під час застосовування контрольних карт можливі два види помилок. Помилка першого роду виникає, коли процес знаходиться в статистично керованому стані, а точка вискакує за контрольні межі випадково. У результаті неправильно вирішують, що процес вийшов зі стану статистичної керованості, і роблять спробу знайти й усунути причину неіснуючої проблеми.
Помилка другого роду виникає, коли розглянутий процес не керований, а точки випадково виявляються усередині контрольних меж. У цьому випадку невірно роблять висновок, що процес статистично керований і упускають можливість попередити ріст виходу невідповідної продукції. Ризик помилки другого роду — функція трьох факторів: ширини контрольних меж, ступеня неке­рованості й обсягу вибірки. їхня природа така, що можна зробити лише загальне твердження про величину помилки.

Система карт Шухарта враховує тільки помилки першого роду, рівні 0,3 % у межах 3σ. Оскільки у загальному випадку недоцільно робити повну оцінку втрат від помилки другого роду в конкретній ситуації, а зручно довільно обирати малий обсяг підгрупи в 4 чи 5 одиниць, доцільно використовувати межі на відстані ±3σ і зосереджувати увагу в основному на керуванні і поліпшенні якості самого процесу.
Якщо процес статистично керований, контрольні карти реалізують метод безупинного статистичного перевіряння нульової гіпотези про те, що процес не змінився і залишається стабільний. Але оскільки величину конкретного відхилення характеристики процесу від цільового значення, яка могла б привернути увагу, звичайно не можна визначати заздалегідь, як і ризик помилки другого роду, і обсяг вибірки не розраховують для досягнення відповідного рівня ризику, то карту Шухарта не варто розглядати для перевіряння гіпотез (див. ISO 7966 та ISO 7870).

Шухарт підкреслював саме емпіричну корисність контрольних карт для встановлення відхилень від стану статистичної керованості, а не їх імовірнісну інтерпретацію. Деякі користувачі все таки застосовують криві оперативних характеристик як засоби для інтерпретації перевірянь гіпотез.

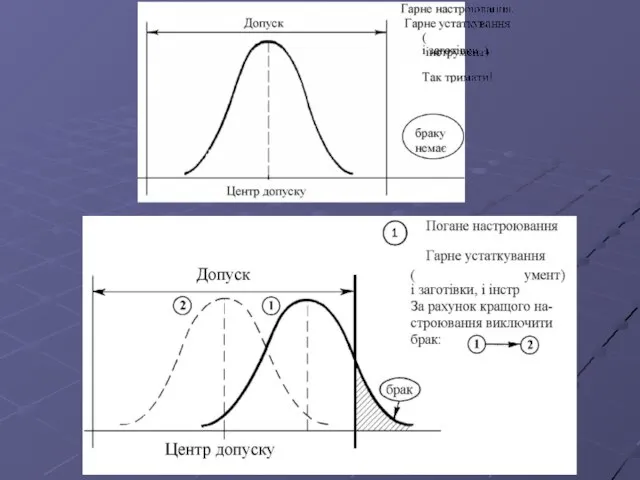
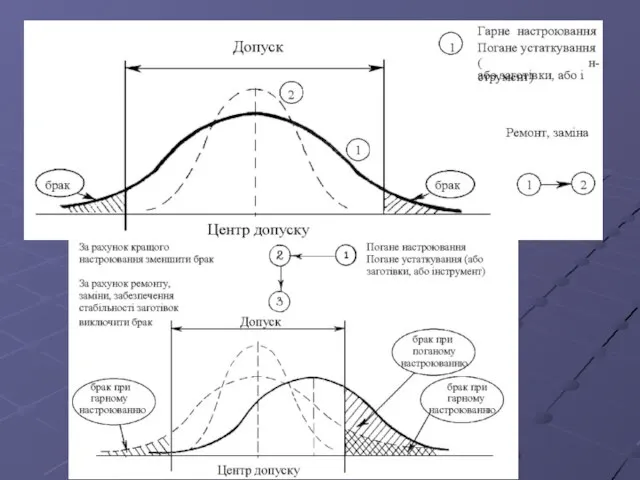
Коли нанесене значення виходить за одну з контрольних меж або серія значень виявляє незвичайні структури відповідний стан не можна далі вважати станом статистичної керованості. У цьому випадку треба дослідити та знайти невипадкові причини, а процес можна зупинити чи скорегувати. Як тільки невипадкові причини знайдено і усунено, процес знову готовий до продовження роботи. Під час виникнення помилки першого роду зрідка можна не знайти ніякої особливої причини, і тоді вважають, що вихід точки за межі являє собою досить рідкісну подію, випадкову причину, яка викликала появу значення поза контрольними межами, навіть коли процес знаходиться в статистично керованому стані.

Якщо контрольну карту процесу будують уперше, то часто трапляється так, що процес статистично некерований. Контрольні межі, які розраховані на основі даних такого процесу, будуть іноді призводити до помилкових висновків, оскільки вони можуть виявитися занадто широкими. Тому перш ніж установлювати постійні параметри контрольних карт, треба привести процес до статистично керованого стану.

ТИПИ КОНТРОЛЬНИХ КАРТ
Контрольні карти Шухарта бувають двох типів: для кількісних і альтернативних даних. Для кожної контрольної карти зустрічаються дві ситуації:
стандартні значення не задано;
стандартні значення задано.
Стандартні значення — це значення, встановлені відповідно до деяких конкретних вимог чи мети.

Контрольні карти, для яких не задано стандартні значення
Мета таких карт — виявити, чи є відхилення значень досліджуваної характеристики, такої як XCP, R чи якої-небудь іншої статистики, лише випадковими. Ці контрольні карти базуються цілком на даних самих вибірок, їх використовують для виявлення змін, які обумовлені невипадковими причинами.

Контрольні карти за наявності заданих стандартних значень
Метою таких карт є визначання того, чи відрізняються значення XCp і т.ін. для декількох підгруп, кожна обсягом n спостережень, від відповідних стандартних значень Хо (чи µо) і т.ін. більше, ніж можна чекати за впливів тільки випадкових причин.
Різниця між картами, для яких задано стандартні значення, і картами, для яких не задано стандартні значення, полягає у додаткових вимогах до центрального значення та варіації процесу.
Встановлені значення можуть базуватися на досвіді, отриманому під час використовування контрольних карт без апріорної інформації, або на заданих стандартних значеннях. Вони також можуть базуватися на економічних показниках, встановлених після розгляду потреби в послузі і вартості виробництва, чи можуть бути зазначені в технічних вимогах на продукцію.

Бажано, щоб встановлені значення визначали на основі дослідження попередніх даних, що, як передбачено, стануть типовими для всіх майбутніх даних. Для ефективного використовування контрольних карт стандартні значення повинні бути зіставлені з природною мінливістю процесу. Контрольні карти, що базуються на таких стандартних значеннях, особливо корисні для керування процесами і підтримки однорідності продукції на бажаному рівні.

Типи контрольних карт для кількісних та альтернативних даних
Розглядають такі контрольні карти:
а) контрольні карти для кількісних даних:
1) карти середнього (Xcp) і розмахів (R) чи вибіркових стандартних відхилень (s);
2) карти індивідуальних значень (X) і ковзних розмахів (R);
3) карти медіан (Ме) і розмахів (R);
б) контрольні карти для альтернативних даних:
1) карти часток невідповідностей (р) чи карти числа невідповідних одиниць (np);
2) карта кількості невідповідностей (с) або карта числа невідповідностей, які приходяться на одиницю продукції (u).

КОНТРОЛЬНІ КАРТИ ДЛЯ КІЛЬКІСНИХ ДАНИХ
Кількісні дані являють собою спостереження, отримані вимірюванням і записуванням значень деякої характеристики для кожної одиниці, розглянутої в підгрупі. Прикладами виміряних значень є довжина в метрах, опір в омах, шум у децибелах тощо. Карти для кількісних даних, особливо найпростіші з них — Xcp - і R-карти, є класичним застосовуванням контрольних карт до статистичного керування процесами.

Контрольні карти для кількісних даних мають такі переваги:
а) Більшість процесів і їхня продукція на виході мають характеристики, що можуть бути виміряні, тому ці карти застосовують частіше.
б) Виміряне значення містить більше інформації ніж просте твердження типу «так чи ні».
с) Поведінка процесу може бути проаналізована без використовування встановлених вимог. Карти запускають разом із процесом і дають незалежну картину того, на що процес здатний. Після цього характеристики процесу можна чи порівнювати, чи не порівнювати зі встановленими вимогами.
d) Хоча одержання кількісних даних дорожче ніж альтернативних, обсяги підгруп для кількісних даних майже завжди набагато менші і у цьому випадку набагато ефективніші. Це дозволяє в деяких випадках знизити загальну вартість контролю і зменшити часовий розрив між виробництвом продукції і коригувальним впливом.

Для контрольних карт, що використовують кількісні дані, передбачено нормальний (гауссівський) розподіл відхилень в межах вибірок, причому відхилення від цього припущення впливають на ефективність карт.
Коефіцієнти для обчислювання контрольних меж виведені за умови нормального розподілу. Оскільки більшість контрольних меж використовують тільки як емпіричні критерії під час прийняття рішень, доцільно нехтувати малими відхилення від нормальності.
У будь-якому разі завдяки центральній граничній теоремі вибіркові середні мають розподіл, що наближається до нормального з ростом обсягу вибірки, навіть коли окремі спостереження не підкоряються нормальному закону; це обґрунтовує можливість припущення про нормальність для Xcp - карт навіть за таких малих обсягів вибірок як 4 чи 5 одиниць, узятих для проведення контролю.

Під час розгляду окремих спостережень для вивчення властивостей процесу важливу роль відіграє його істинний розподіл. Рекомендовано періодично перевіряти виконання таких припущень, щоб переконатися, що використовувані дані належать одній сукупності. Треба зазначити, що розподіли розмахів і стандартних відхилень відрізняються від нормального, хоча припущення нормальності використовували під час оцінювання коефіцієнтів для обчислювання контрольних меж, які, як правило, прийнятні для процедур прийняття емпіричних рішень.

Карти середніх (XCP) та розмахів (R) або вибіркових стандартних відхилень (s)
Карти для кількісних даних можуть описувати вибіркові дані процесу через розкид (мінливість від одиниці до одиниці) і через положення центра (середнє процесу). Тому контрольні карти для кількісних даних майже завжди застосовують і аналізують парами - одна карта для положення центра й одна - для розкиду. Найчастіше використовують пари XCP - та R-карт. У таблицях 1 і 2 наведено формули контрольних меж і коефіцієнти для відповідних карт.

Таблиця 1 — Формули контрольних меж для карт Шухарта з використовуванням кількісних даних

Таблиця 2 — Коефіцієнти для обчислювання ліній контрольних карт

Контрольні карти для індивідуальних значень (X)
У деяких ситуаціях для керування процесами неможливо або непрактично мати справу з ра­ціональними підгрупами. Час або вартість, необхідні для вимірювання за одиночного спостереження, настільки великі, що проведення повторних спостережень навіть не розглядають. Це звичайно відбувається, коли вимірювання дорого коштує (наприклад, за руйнівного контролю) або вихід продукції весь час відносно однорідний. В інших ситуаціях можливо отримати тільки одне значення, наприклад покази приладу або значення характеристики партії вихідних матеріалів. У таких випадках необхідно, щоб контроль процесу базувався на індивідуальних значеннях.
У випадку карт індивідуальних значень для одержання оцінок мінливості в межах партії не використовують раціональні підгрупи, а контрольні межі розраховують на основі міри варіації, отриманої за ковзними розмахами, часто двох спостережень.

Ковзний розмах — це абсолютне значення різниці вимірювань в послідовних парах; тобто це різниця першого і другого вимірювання, потім другого і третього тощо.
У таблиці 3 приведено формули для розрахунку контрольних меж для карт, індивідуальних значень.

Таблиця 3 — Формули контрольних меж для карт індивідуальних значень

Під час використовування карт індивідуальних значень необхідно враховувати таке:
карти індивідуальних значень не так чутливі до змін процесу, як ХСР - та R - карти;
під час інтерпретації карт індивідуальних значень потрібно виявляти обережність, якщо роз­поділ процесу не є нормальним;
карти індивідуальних значень не вирізняють повторюваність процесу від елементу до еле­менту, і тому в деяких випадках краще використовувати звичайні ХСР – та R - карти з малими обсягами вибіркових підгруп (від 2 до 4), навіть якщо це вимагає збільшення інтервалу між підгрупами.

Контрольні карти для медіан (Ме)
Карти медіан є альтернативою – XCP - та R-карт для керування процесом з вимірюваними да­ними; вони забезпечують аналогічні висновки і мають певні переваги. Такі карти прості під час застосовування і не вимагають великих обчислювань. Це може полегшити їх впровадження у виробництво. Оскільки на карти наносять значення медіан нарівні з індивідуальними значеннями, карта медіан дає розкид результатів процесу і докладну картину варіацій.
Контрольні межі для карт медіан обчислюють двома способами: за допомогою розрахунку медіан від медіан підгруп і медіан розмахів; або розрахунку середніх від медіан підгруп і середніх розмахів. Лише останній спосіб, який і простіший, і зручніший, розглядають в цьому стандарті.

Контрольні межі розраховують таким чином
Карта медіан

Карта розмахів

МЕТОД КЕРУВАННЯ ТА ІНТЕРПРЕТАЦІЯ КОНТРОЛЬНИХ КАРТ ДЛЯ КІЛЬКІСНИХ ДАНИХ

Це міра слушності (конзистентності) і однорідності процесу. Якщо R-карта показує, що варіації всередині підгруп не змінюються, то це означає, що процес залишається в статистично керованому стані. Це має місце тільки в тому випадку, якщо всі вибірки обробляли однаково. Якщо R-карта показує, що процес вийшов з керованого стану або рівень на R-карті зростає, то це може означати, що або окремі підгрупи зазнали різного обробляння, або в процесі діє декілька різних систем причинно-наслідкових зв'язків.

Треба слідувати наступній процедурі керування
Збирають і аналізують дані, обчислюють середні і розмахи.
Спочатку будують R-карту. Зіставляють нанесені точки розмахів зі контрольними межа­ми, виділяють точки поза межами, незвичайні структури або тренди. Для кожного сигналу про наявність невипадкової причини в значеннях розмаху аналізують операції процесу, щоб визначити причину. Проводять корегувальні дії і дії щодо запобігання повторенню даної причини.

Коли розмахи знаходяться в статистично керованому стані, розкид процесу (відхилення всередині підгруп) вважають стабільним. У цьому випадку можна проаналізувати середні, щоб побачити, чи міняється у часі середнє значення процесу.

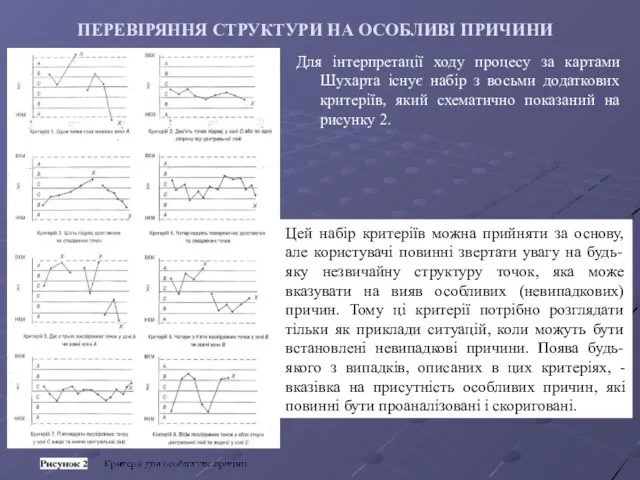
ПЕРЕВІРЯННЯ СТРУКТУРИ НА ОСОБЛИВІ ПРИЧИНИ
Для інтерпретації ходу процесу за картами Шухарта існує набір з восьми додаткових критеріїв, який схематично показаний на рисунку 2.
Цей набір критеріїв можна прийняти за основу, але користувачі повинні звертати увагу на будь-яку незвичайну структуру точок, яка може вказувати на вияв особливих (невипадкових) причин. Тому ці критерії потрібно розглядати тільки як приклади ситуацій, коли можуть бути встановлені невипадкові причини. Поява будь-якого з випадків, описаних в цих критеріях, - вказівка на присутність особливих причин, які повинні бути проаналізовані і скориговані.

КЕРУВАННЯ ПРОЦЕСОМ І МОЖЛИВОСТІ ПРОЦЕСУ
Призначення системи керування процесом полягає в отриманні статистичного сигналу про наявність особливих (невипадкових) причин варіацій. Систематичне усунення особливих причин надмірної мінливості приводить процес в стан статистичної керованості. Якщо процес знаходиться в статистично керованому стані, якість продукції можна передбачувати, і процес придатний для задоволення вимог, встановлених в нормативних документах.
Можливості процесу визначають повною мінливістю (розкидом процесу), зумовленою звичайними причинами, тобто мінімальною мінливістю, яка залишається після усунення всіх невипадкових причин. Можливості процесу представляють показники самого процесу в статистично керованому стані. Процес спочатку приводять в такий стан, а потім визначають його можливості.

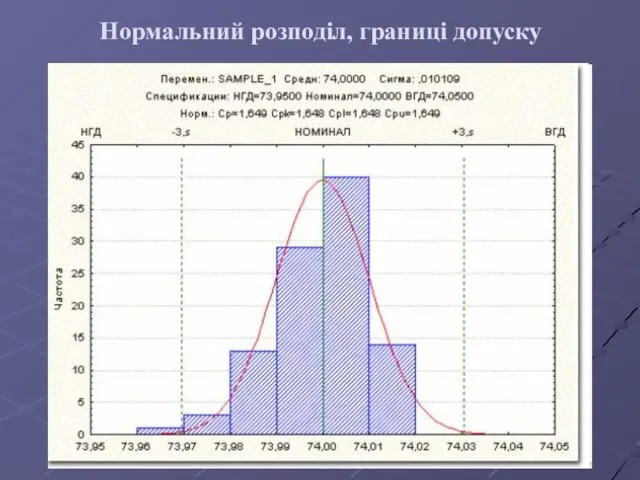
У загальному випадку можливості процесу визначають індексом можливостей процесу IМП (чи ср):
де ВПЗ — верхнє максимально припустиме значення параметра, яке контролюють, НПЗ — нижнє максимально припустиме значення параметра, яке контролюють,
σ — оцінюють за середньою мінливістю всередині підгруп і виражають
ІМП = номінальний допуск / розкид процесу =
= (ВПЗ- НПЗ)/ 6σ,
Нижня/верхня потенційна придатність: Cpl, Cpu.
Cpl = (Середнє - НПЗ)/3σ и Cpu = (ВПЗ - Середнє)/3σ

Нормальний розподіл, границі допуску

Потрібно зазначити, що ІМП вимірює тільки відношення розкиду процесу і допуску, а положення або центрування процесу не враховують. За високих значень ІМП все-таки можливий вихід частки значень за встановлені межі. Тому важливо також оцінювати відстань між середнім значенням процесу і найближчим гранично допустимим значенням.
За ІМП, меншому ніж 1, можливості процесу неприйнятні, а за ІМП, що дорівнює 1, процес знаходиться на межі потрібних можливостей. На практиці як мінімальне прийнятне значення беруть ІМП = 1,33, оскільки завжди є деякі варіації у вибірках та немає процесів, які завжди знаходяться в статистично керованому стані.

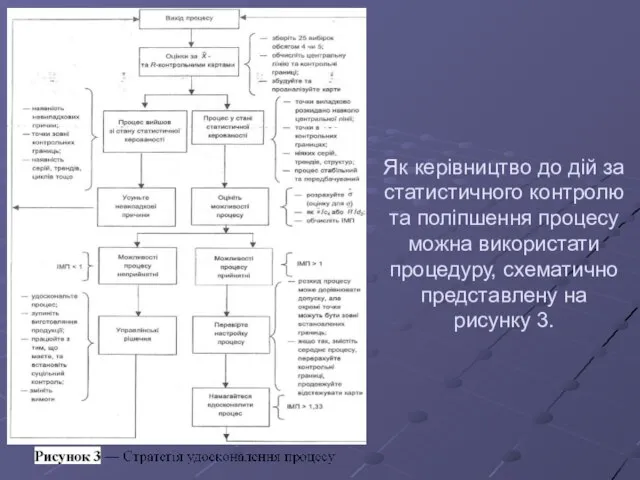
Як керівництво до дій за статистичного контролю та поліпшення процесу можна використати процедуру, схематично представлену на рисунку 3.

Явище самоорганізації і його застосування при вирішенні завдань менеджменту якості
У результаті досліджень процесів створення продукції визначені особливості виробничої системи за критеріями спадковості:
а) якість – функція організованості структури процесів створення продукції;
б) виникнення відмов обумовлене негативною спадковістю виробництва, нагромадженням її на стадіях життєвого циклу;
в) як міру організованості структури виробництва приймаємо ентропію виробничої системи; ентропія, у свою чергу, – це функція ступеню дефектності процесів створення продукції;
г) ентропія оцінюється рівнем дефектності на етапах створення продукції або в процесі технологічних операцій (переходів);
д) заходи, що знижують рівень дефектності, – суть керуючі впливи, що підвищують організованість системи.

Відкрита інформаційна система, зв’язана з зовнішнім світом, відкіля надходить потік енергії (інформації), що стимулює внутрішні процеси перетворення системи, що викликають її оновлення, у вигляді створення нової продукції.
Оновлення системи сприяє убуванню ентропії, що означає процвітання компанії.
Неадекватна реакція фірм на зміни в зовнішньому світі (зміни вимог споживача) веде до збільшення ентропії і деградації виробничої системи. Навіть компанія, що має довгу історію успішного функціонування, має потребу в припливі свіжої управлінської енергії у свої елементи, щоб зупинити невблаганні сили руйнування.

Управління процесом і відтворюваність процесу

Напрямок процесів виникнення відмов у процесі роботи виробу, відповідно до другого закону термодинаміки, вказує на зростання ентропії системи. У цій асиметричності власних процесів, що відбуваються, криється причина психологічного розрізнення минулого і майбутнього. Такий висновок дуже важливий для розуміння фізичної природи відмов і ролі етапів створення виробів у процесах формування рівня надійності.

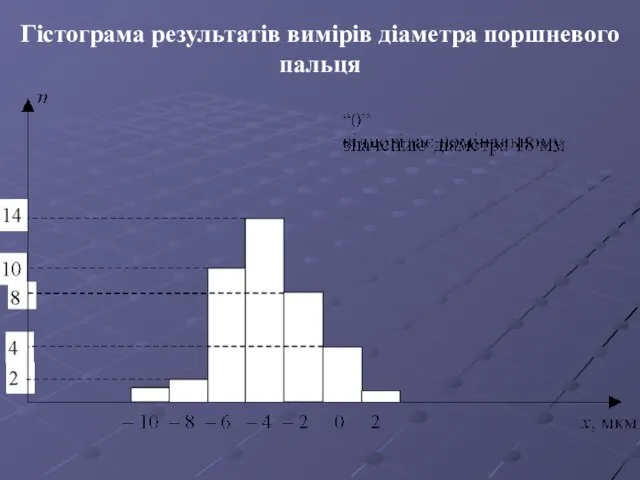
Гістограма результатів вимірів діаметра поршневого пальця

Варіації: звичайні та особливі причини

Частки розподілу

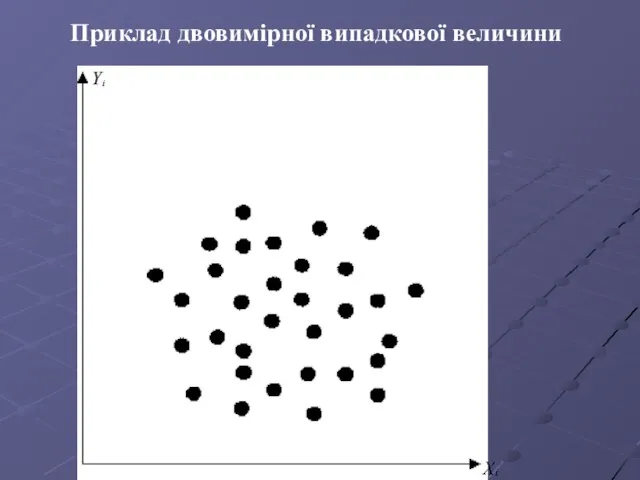
Приклад двовимірної випадкової величини