Кредитные расчеты

D – величина займа;
n – срок кредита;
i – процентная ставка
Сам займ D называют основным долгом, наращиваемый добавок – процентными деньгами.

1. Погашение займа одним платежом в конце срока.
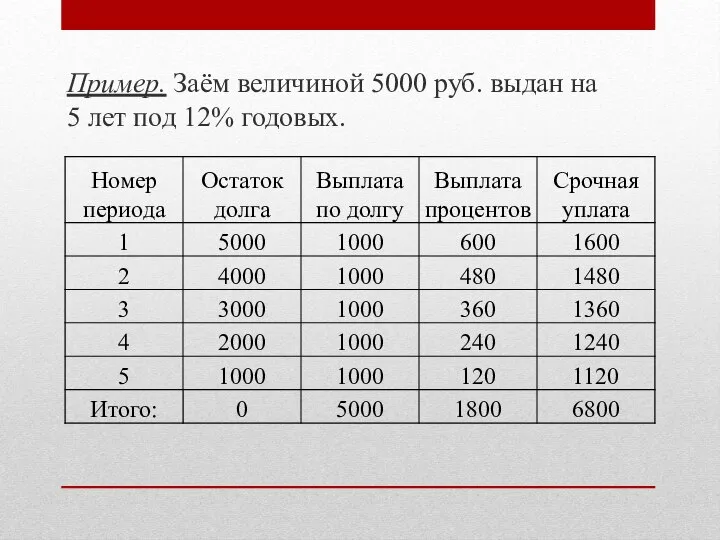
Пример. Заём величиной 5000 руб. выдан на 5 лет под 12% годовых.
Тогда величина погашающего платежа составит

2. Погашение основного долга одним платежом в конце срока.
Проценты за первый год: ;
проценты за второй год: …
Платеж в конце года n: .
Пример. Заём величиной 5000 руб. выдан на 5 лет под 12% годовых.

3. Погашение основного долга равными годовыми выплатами.
Ежегодная выплата основного долга:
Платеж в конце первого года:
Платеж в конце второго года:
Платеж в конце года k:
Платеж в конце года n:

Пример. Заём величиной 5000 руб. выдан на
5 лет под 12% годовых.

4. Погашение займа равными годовыми выплатами.
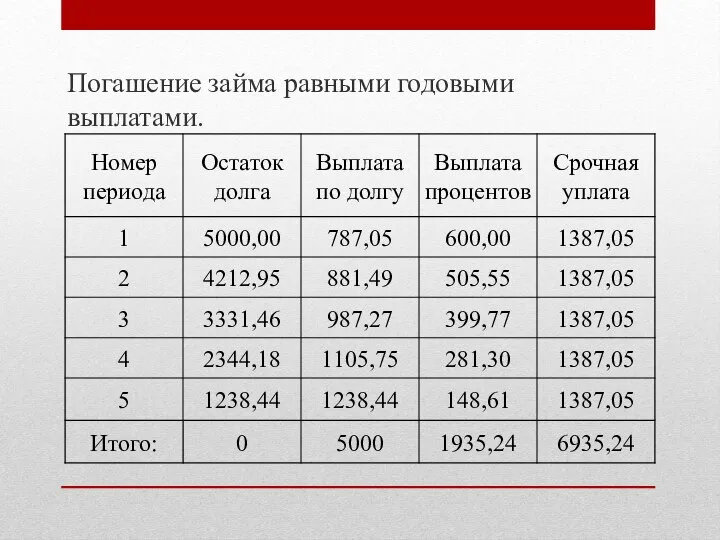
Пример. Заём величиной 5000 руб. выдан на 5 лет под 12% годовых.

Погашение займа равными годовыми выплатами.

Некоторые закономерности:
Оплаченная часть долга:
Остаток долга:

Если заданы расходы по обслуживанию долга (т.е. R), то срок погашения:
(решение существует при Di/R< 1)

Пример. Выдан кредит в размере 1000 тыс. руб. под 10% годовых. Для его погашения предполагается выделять сумму порядка
200 тыс. руб. в год. Каков срок погашения кредита?
Решение.
Если n =7, то R =1000/a(7,10)= 205,406 тыс. руб.
Или при R = 200, n = 7 R7 = 251,28 тыс. руб.

Общий метод погашения займа.
D – величина займа;
n – срок кредита;
i – процентная ставка

Заём выдан на 2 года.
Выплаты в конце 1го года: D1+iD.
Выплаты в конце 2го года: D2 = D – D1; I2=iD2.

D1, D2, …, Dn – платежи в счет основного долга D;
I1, I2, …, In – процентные платежи, начисленные на остаток долга.

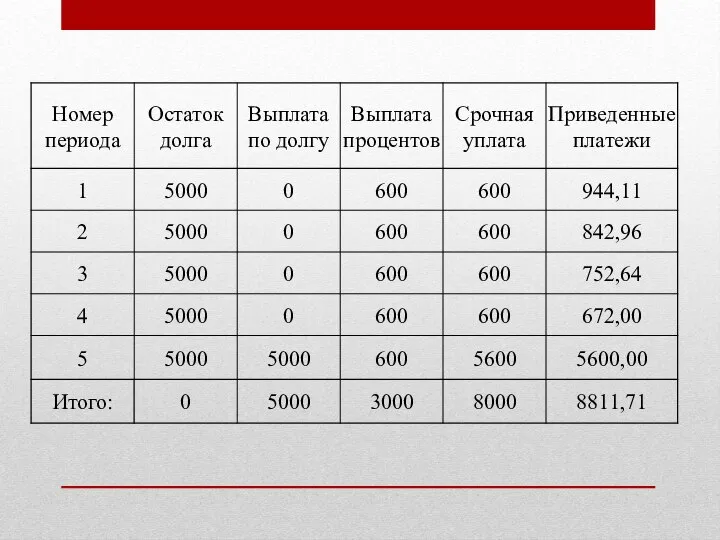
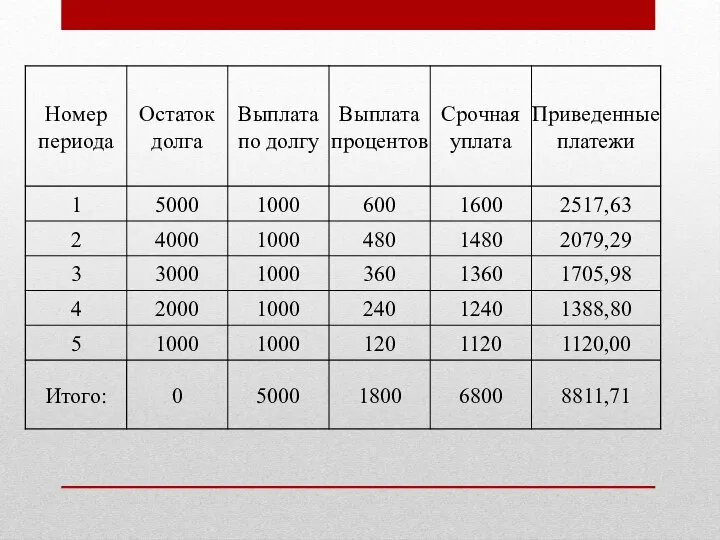
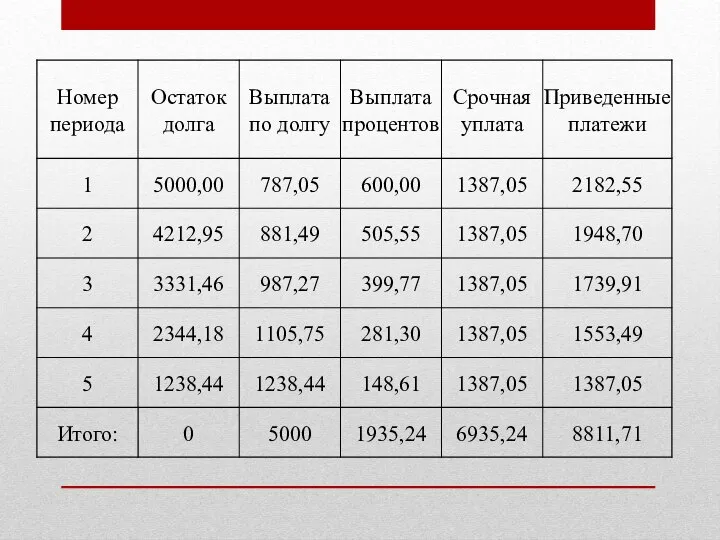
Проверим полученное практическими расчетами, для этого пересчитаем стоимость периодических платежей на конец 5го года (D = 5000 руб., n = 5 лет, i = 12% годовых).

Потребительский кредит и
его погашение
При выдаче потребительского кредита сразу на всю сумму кредита начисляются простые проценты, они прибавляются к величине самого кредита и сумма всех погашающих выплат должна быть равна этой величине. Существует несколько схем погашения потребительского кредита.

Потребительский кредит.
Погашение равными выплатами.
Пусть кредит размером D взят на п лет, годовая ставка простых процентов i.
Всего надо набрать выплат на сумму D(1+ ni).
Если в год предусмотрено (договором о кредите) т выплат, то одна выплата равна
D(1+ ni)/nm.

Пример. Заём величиной 5000 руб. выдан на
5 лет под 12% годовых.
Решение.
D(1+ ni) = 5000·(1+5·0,12) = 8000 руб.
Ежегодная выплата составит
8000/5 = 1600 руб.
Если предусмотрены ежемесячные выплаты, то величина разового (месячного) платежа составит 8000/(12·5) = 133,33 руб.

Какова ставка сложного процента, при которой современная величина выплат по кредиту равна его номинальной величине? Обозначим ее j. Имеем уравнение

Для случая ежегодных выплат имеем:
1600·a(5, j) = 5000; a(5, j) = 5000/1600 = 3,125;
j = 18%
[=СТАВКА(5; -1600; 5000)].
Для случая ежемесячных выплат имеем:
133,33·a(5·12, jm)= 5000;
a(60, jm)= 5000/133,33= 37,5; jm = 1,69%
[=СТАВКА(60; -133,33; 5000)].
Годовая ставка j = jm ·12= 20,31%.
Эффективная ставка равна 22,31%.

Потребительский кредит. Правило 78.
Долг D выплачивается равными долями, проценты Dni – выплатами, уменьшающимися в арифметической прогрессии, последняя выплата равна разности этой прогрессии.
m – число выплат в году;
d – величина последней выплаты;
mnd – величина первой выплаты.

N – сумма номеров всех выплат;
1я выплата – mn таких частей;
2я выплата – (mn – 1) таких частей;
…
Последний платеж – одна часть.

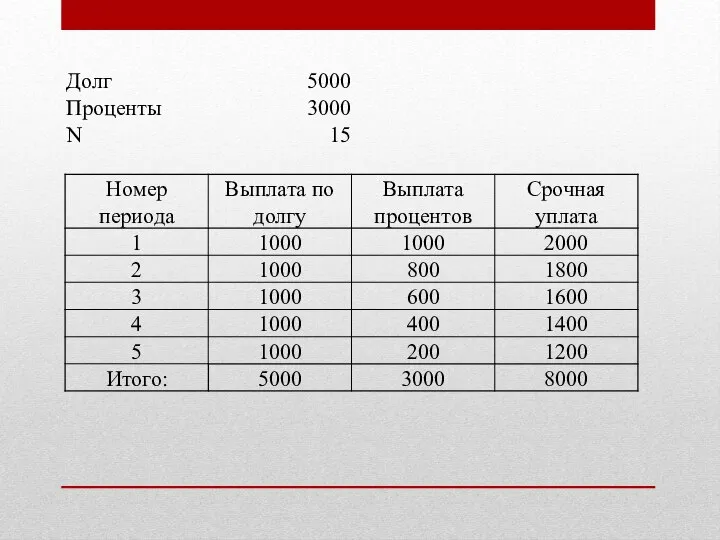
Пример. Заём величиной 5000 руб. выдан на
5 лет под 12% годовых.
Dni =3000 руб.
N=1+2+3+4+5=15

Для расчета ставки сложного процента j можно воспользоваться функцией MS Excel ВСД:
=ВСД({-5000:2000:1800:1600:1400:1200})
( j = 20%)

Льготные кредиты
Пусть кредит размером D выдан на п лет по льготной ставке g, меньшей обычной ставки i, и будет погашаться равными выплатами у:
А если бы выплаты шли по обычной ставке i, то размер каждой выплаты составлял бы

Разность z – у = D/a(n, i) – D/a(n, g) – это ежегодные потери кредитора,
а современная величина ренты этих потерь
по действующей ставке i, т.е.
(z – у)·а(п, i) = [D/а(п, i) – D/a(n, g)]· a(n, i) =
=D [1 – а(п, i)/a(n, g)] – абсолютный грант-элемент (субсидия кредитора заемщику).
[1 – а(п, i)/a(n, g)] – относительный грант-элемент.
Наращенная сумма абсолютного грант-элемента (наращенная сумма субсидии) называется общими потерями кредитора.

Пример. Пусть D = 1000, п = 8, i = 8%, g = 5%.
Находим выплаты по обычной ставке:
z·a(8, 8) = 1000, z =1000/ 5,747; z = 174.
Выплаты по льготной ставке:
y·a(8, 5) = 1000, y=1000/6,463; y = 155.
Ежегодные потери кредитора z - y = 19.
Относительный грант-элемент:
1-5,747/6,463=0,111.
Абсолютный грант-элемент: 1000·0,111 = 111.
Общие потери кредитора: 111·(1+0,08)8 = 205

Погашение традиционной ипотечной ссуды
Традиционная ипотечная ссуда погашается равными ежемесячными выплатами, на которые ежемесячно же начисляются проценты.
Пусть ссуда D выдана на срок п лет под годовую ставку сложных процентов i.
Равные ежемесячные выплаты размером у образуют ренту с частотой платежей и начислением процентов 12 раз в году.