Круги Эйлера

Леонард Эйлер
ИДЕАЛЬНЫЙ МАТЕМАТИК
XVIII ВЕКА
(к 300-летию со дня рождения)

Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера. В Энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера.

"Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе...", где появились впервые «круги Эйлера»

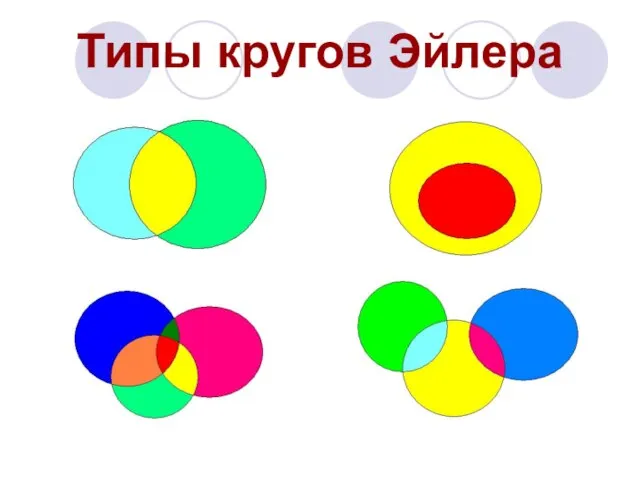
Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».

Типы кругов Эйлера

Множество чисел
Множество всех действительных чисел Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.

Решение задач с помощью кругов Эйлера.
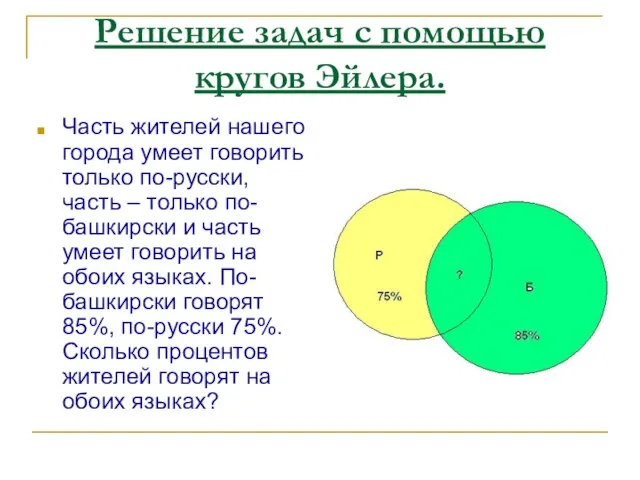
Часть жителей нашего города умеет говорить только по-русски, часть – только по-башкирски и часть умеет говорить на обоих языках. По-башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение:
100%-85%=15% (жителей говорят только по-русски)
75%-15%=60% (жителей говорят на обоих языках)

Задача 2. О подругах
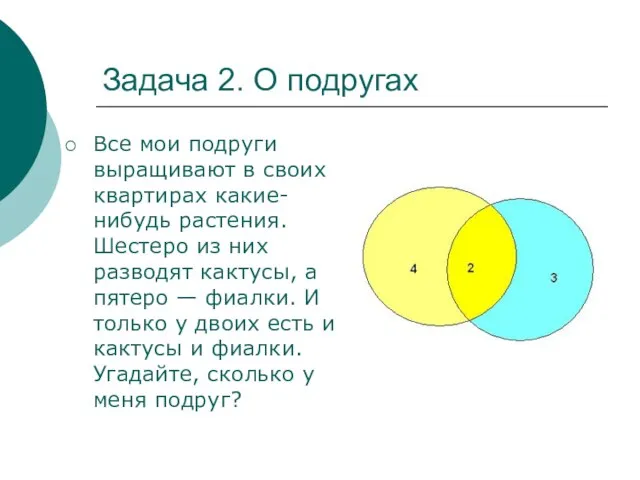
Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?

Спортивная задача
В футбольной команде «Баймак» 30 игроков:
18 нападающих.
11 полузащитников,
17 защитников
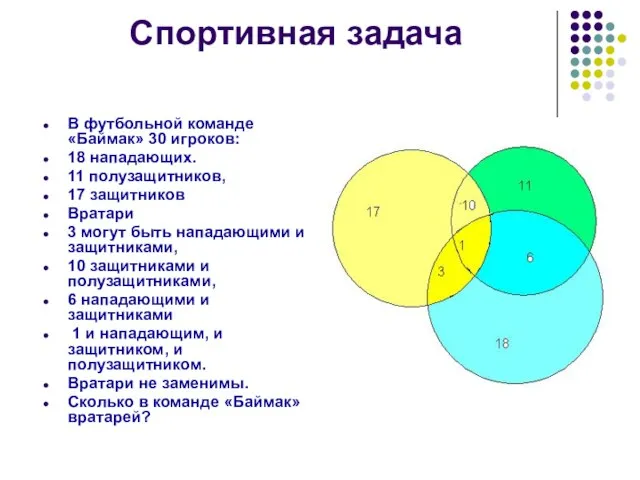
Вратари
3 могут быть нападающими и защитниками,
10 защитниками и полузащитниками,
6 нападающими и защитниками
1 и нападающим, и защитником, и полузащитником.
Вратари не заменимы.
Сколько в команде «Баймак» вратарей?

Решение
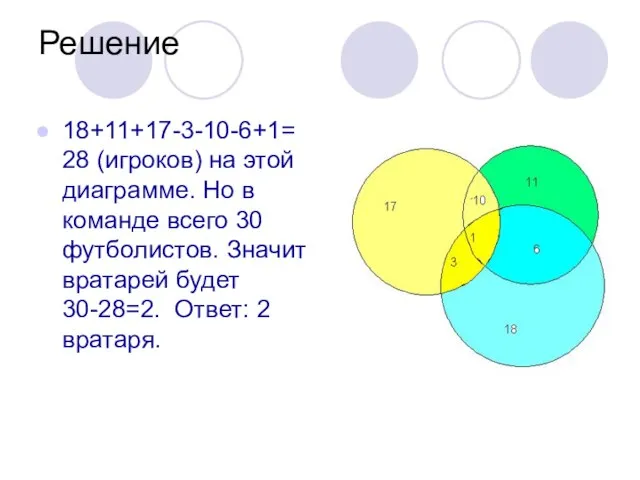
18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.

«Озеро Графское»
Из 100 отдыхающих на турбазе «Графское»,
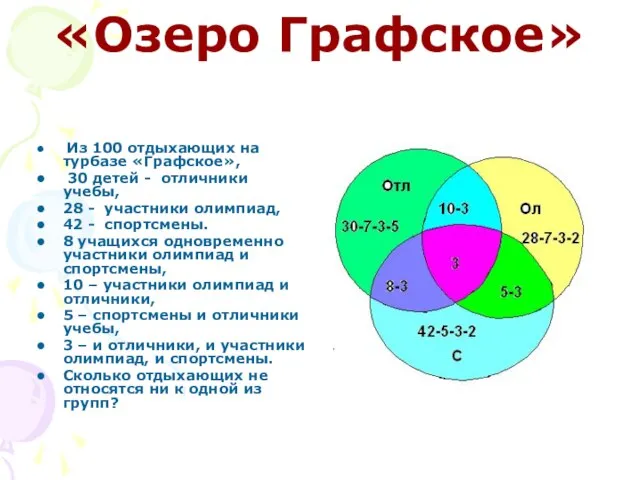
30 детей - отличники учебы,
28 - участники олимпиад,
42 - спортсмены.
8 учащихся одновременно участники олимпиад и спортсмены,
10 – участники олимпиад и отличники,
5 – спортсмены и отличники учебы,
3 – и отличники, и участники олимпиад, и спортсмены.
Сколько отдыхающих не относятся ни к одной из групп?

Решение
20+13+30+3+5+7+2=80 (детей)
100-80=20 (детей не входят ни в одну из групп)
Ответ: 20 детей.