Слайд 2Определение
Квадратичной функцией называется функция, которую можно задать формулой вида y=ax2+bx+c, где

x-независимая переменная, a, b и c-некоторые числа, причём a=0.
Графиком является парабола.
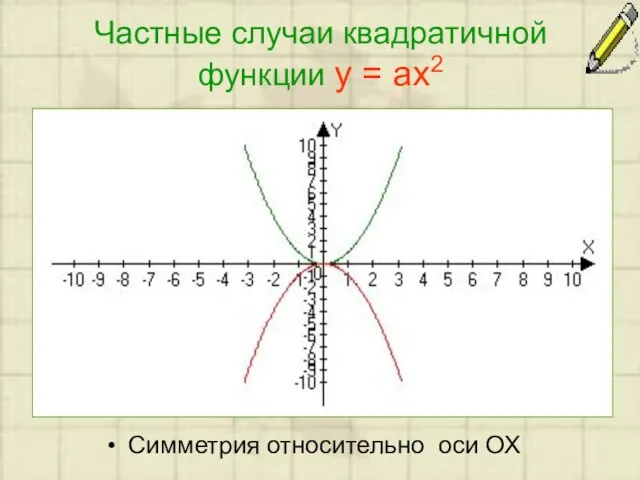
Слайд 3Частные случаи квадратичной функции y = ax2
Симметрия относительно оси ОХ
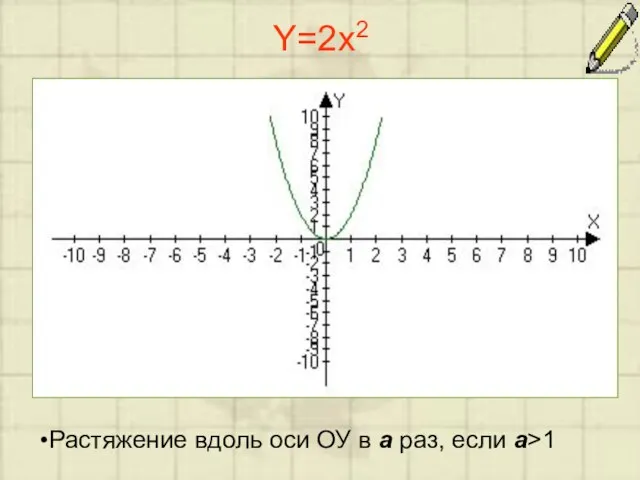
Слайд 4Y=2x2
Растяжение вдоль оси ОУ в a раз, если a>1
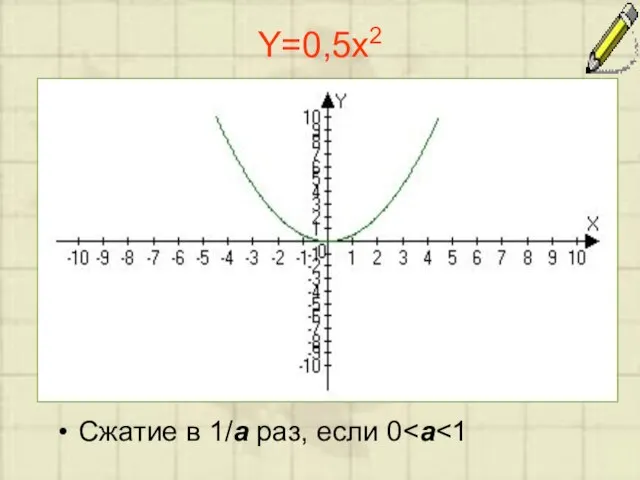
Слайд 5Y=0,5x2
Сжатие в 1/a раз, если 0
Слайд 6Графики функций у=ах2+n
Сдвиг вдоль оси ОУ на n единиц вверх, если n
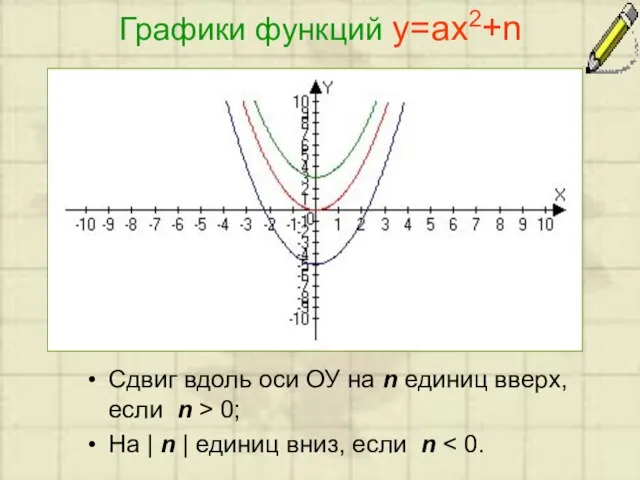
> 0;
На | n | единиц вниз, если n < 0.
Слайд 7Графики функций у = а(х-m)2
Сдвиг вдоль оси ОХ на m единиц вправо,
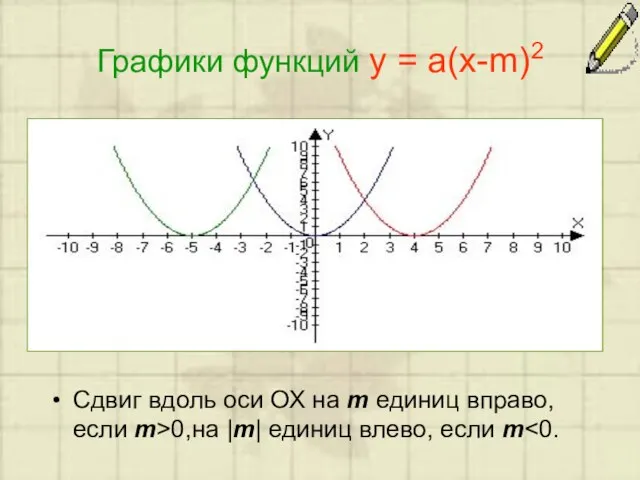
если m>0,на |m| единиц влево, если m<0.
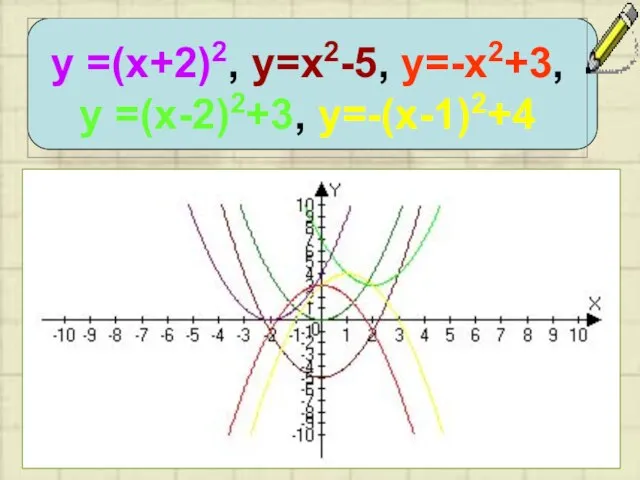
Слайд 8у =(х+2)2, у=х2-5, у=-х2+3,
у =(х-2)2+3, у=-(х-1)2+4
Слайд 9Построение графика квадратичной функции у=ах2+bx+c
Определить направление ветвей параболы.
Если а>0,ветви параболы направлены вверх.

Если а<0,ветви параболы направлены вниз.
2. Найти координаты вершины параболы А(m ; n).
m= -b / 2a , n= y (m)
3. Написать уравнение оси симметрии х =m.
4. Составить таблицу дополнительных значений с учётом оси симметрии.








 http://cde.sssu.ru
http://cde.sssu.ru Австрия. Конституционные основы судебной власти
Австрия. Конституционные основы судебной власти Кризис 3-х лет
Кризис 3-х лет Неповторимая планета Земля
Неповторимая планета Земля Работа с проблемными детьми.
Работа с проблемными детьми. Игра
Игра Потомки Н. В. Гоголя
Потомки Н. В. Гоголя Русь в XIII – XV веках Монгольское нашествие на Русь
Русь в XIII – XV веках Монгольское нашествие на Русь Комплекс упражнений для физкультпаузы
Комплекс упражнений для физкультпаузы Видеорегистратор. Видеокамера
Видеорегистратор. Видеокамера Готовое решение для увеличения доходности и контроля клиентской базы дилерского центра Subaru. Генезис
Готовое решение для увеличения доходности и контроля клиентской базы дилерского центра Subaru. Генезис Трудные времена на Русской земле
Трудные времена на Русской земле Как дешевле покупать пищевые продукты?
Как дешевле покупать пищевые продукты? Аналитико-сетевой коучинг ©
Аналитико-сетевой коучинг © Программа поддержки многодетных семей в РФ
Программа поддержки многодетных семей в РФ Бизнес-планирование производственной деятельности
Бизнес-планирование производственной деятельности Бортникова С.Л.Право
Бортникова С.Л.Право МИРОВОЕ СООБЩЕСТВО ГОСУДАРСТВ
МИРОВОЕ СООБЩЕСТВО ГОСУДАРСТВ Pets and Other Animals
Pets and Other Animals Художники-юбиляры 2020 год
Художники-юбиляры 2020 год Разделение под действием сил разности давления
Разделение под действием сил разности давления Голосовая/факсимильная почта (ГФП)
Голосовая/факсимильная почта (ГФП) Спортивный контракт профессионального футболиста с позиции Спортсмен-Мини-Футбольный клуб
Спортивный контракт профессионального футболиста с позиции Спортсмен-Мини-Футбольный клуб ГРУППА КОМПАНИЙ «ДЖЕНСЕР» ВЕКСЕЛЬНАЯ ПРОГРАММА Информационный меморандум ОРГАНИЗАТОР, АНДЕРРАЙТЕР И ПЛАТЕЖНЫЙ АГЕНТ КБ «ЛОКО-Б
ГРУППА КОМПАНИЙ «ДЖЕНСЕР» ВЕКСЕЛЬНАЯ ПРОГРАММА Информационный меморандум ОРГАНИЗАТОР, АНДЕРРАЙТЕР И ПЛАТЕЖНЫЙ АГЕНТ КБ «ЛОКО-Б Матрицы и действия с ними
Матрицы и действия с ними Основы обеспечения безопасности военной службы. Тема 1
Основы обеспечения безопасности военной службы. Тема 1 Самое удивительное животное
Самое удивительное животное  Интенсив только для женщин Настоящая Я
Интенсив только для женщин Настоящая Я