Попов Алексей ПетровичЛАЗЕРНАЯ ДИАГНОСТИКА СИЛЬНОРАССЕИВАЮЩИХ СРЕД И ИЗМЕНЕНИЕ ИХ ОПТИЧЕСКИХ СВОЙСТВПУТЕМ ИМПЛАНТАЦИИ НАНОЧА

СОДЕРЖАНИЕ
Введение
Глава 1. Прохождение сверхкороткого лазерного импульса через случайную среду
Глава 2. Моделирование распространения сверхкороткого лазерного импульса в среде с сильным рассеянием методом Монте-Карло
Глава 3. Метод лазерной импульсной времяпролетной фотометрии как инструмент диагностики сред с сильным рассеянием
Глава 4. Изменение оптических свойств сред с сильным рассеянием в УФ-диапазоне путем имплантации наночастиц диоксида титана
Заключение
Список литературы

Глава 1. Нестационарное уравнение теории переноса излучения
- лучевая интенсивность в точке в направлении, Вт·м-2·ср-1;
- фазовая функция рассеяния;
μs – коэффициент рассеяния (величина, характеризующая среднее
количество актов упругого рассеяния, в которых участвует фотон при
пробеге на единицу длины);
μa – коэффициент поглощения (величина, обратная расстоянию,
на котором интенсивность уменьшается за счет поглощения в е раз);
μt = μs + μa – коэффициент экстинкции;
dΩ′ - единичный телесный угол в направлении;
μs / μt ≡ Λ – альбедо единичного рассеивателя;
t – время;
c – скорость света в среде;
f(t, t΄) – описывает временную деформацию δ-образного импульса
после единичного акта рассеяния.

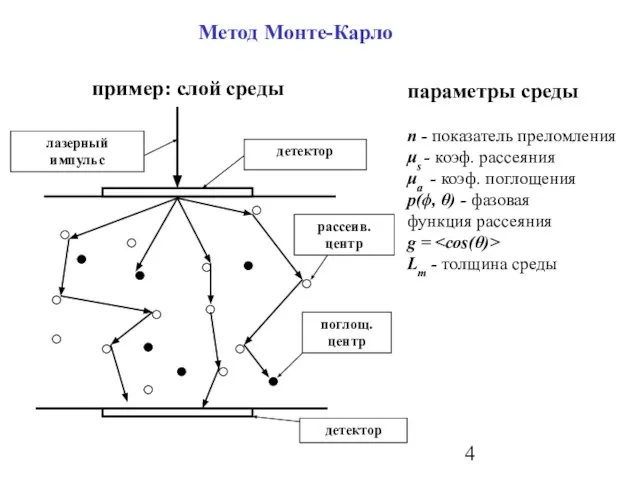
Метод Монте-Карло
пример: слой среды
параметры среды
n - показатель преломления
μs - коэф. рассеяния
μa - коэф. поглощения
p(ϕ, θ) - фазовая
функция рассеяния
g =
Lm - толщина среды

исследовать возможность регистрации параметров рассеянного
в переднее полупространство импульса в зависимости от оптических
свойств и геометрических параметров среды, а также от длительности
зондирующего импульса;
изучить возможность использования сверхкоротких лазерных импульсов
для диагностики сред с сильным рассеянием на примере среды,
имитирующей кожу с разной концентрацией глюкозы; определить
параметры рассеянного импульса, наиболее чувствительные для
мониторинга изменений содержания глюкозы в физиологическом
диапазоне концентраций;
разработать методику определения размеров наночастиц, наиболее
эффективно ослабляющих УФ-излучение при его распространении
в среде, имитирующей кожу человека, а также метод расчета
пропускания, отражения и поглощения света в среде с наночастицами.
ЗАДАЧИ

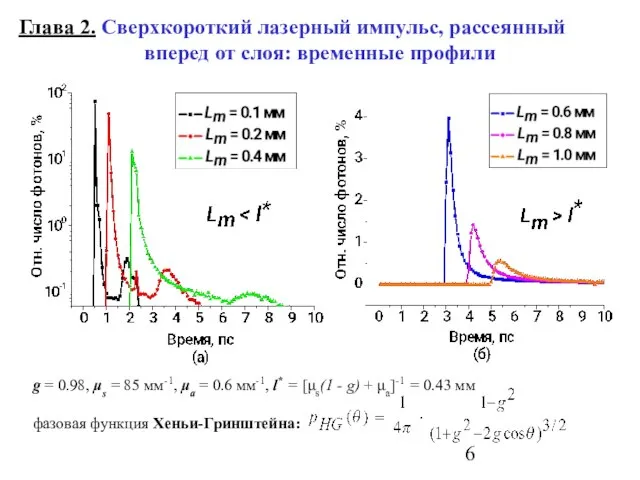
Глава 2. Сверхкороткий лазерный импульс, рассеянный
вперед от слоя: временные профили
g = 0.98, μs = 85 мм-1, μa = 0.6 мм-1, l* = [μs(1 - g) + μa]-1 = 0.43 мм
фазовая функция Хеньи-Гринштейна:

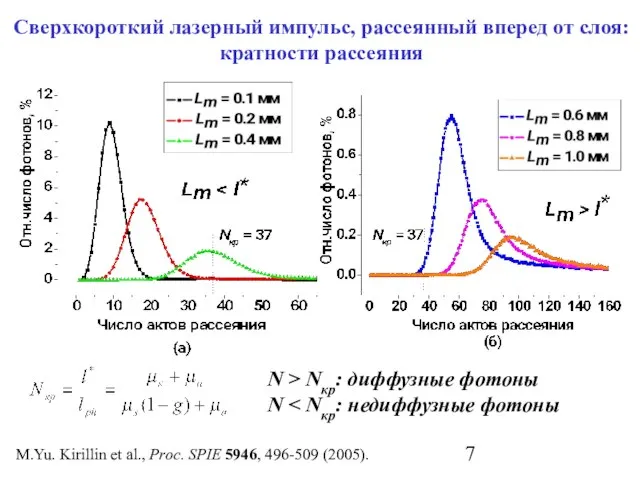
Сверхкороткий лазерный импульс, рассеянный вперед от слоя:
кратности рассеяния
N > Nкр: диффузные фотоны
N < Nкр: недиффузные фотоны
M.Yu. Kirillin et al., Proc. SPIE 5946, 496-509 (2005).

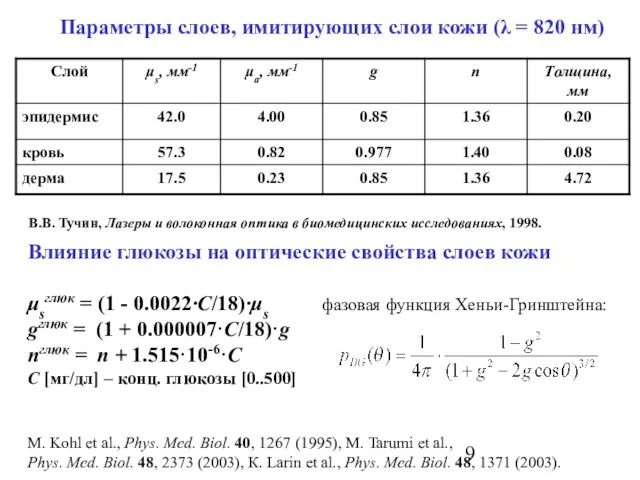
Параметры слоев, имитирующих слои кожи (λ = 820 нм)
В.В. Тучин, Лазеры и волоконная оптика в биомедицинских исследованиях, 1998.
Влияние глюкозы на оптические свойства слоев кожи
μsглюк = (1 - 0.0022·C/18)·μs фазовая функция Хеньи-Гринштейна:
gглюк = (1 + 0.000007·C/18)·g
nглюк = n + 1.515·10-6·C
C [мг/дл] – конц. глюкозы [0..500]
М. Kohl et al., Phys. Med. Biol. 40, 1267 (1995), М. Tarumi et al.,
Phys. Med. Biol. 48, 2373 (2003), К. Larin et al., Phys. Med. Biol. 48, 1371 (2003).

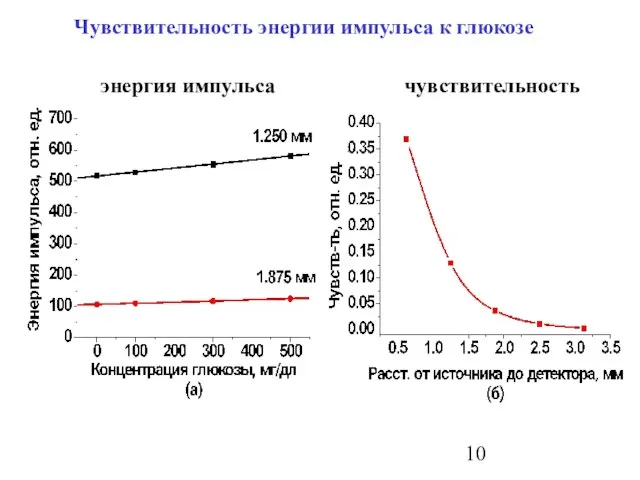
Чувствительность энергии импульса к глюкозе
:
энергия импульса
чувствительность

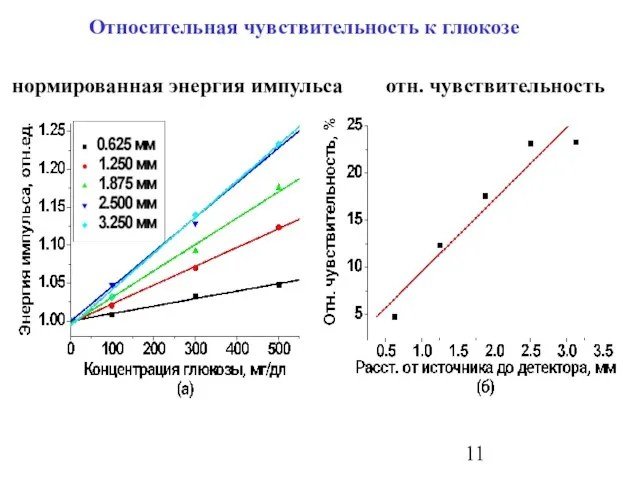
нормированная энергия импульса
отн. чувствительность
Относительная чувствительность к глюкозе

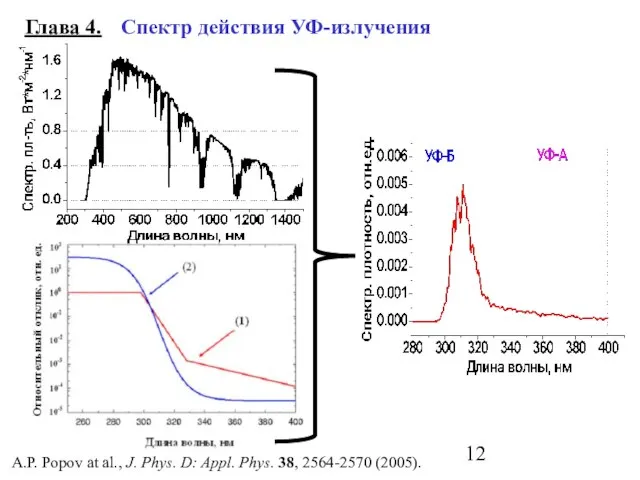
Глава 4. Спектр действия УФ-излучения
A.P. Popov at al., J. Phys. D: Appl. Phys. 38, 2564-2570 (2005).

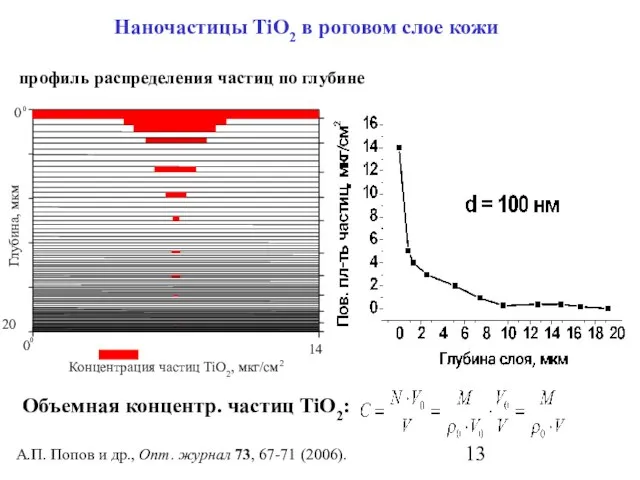
Наночастицы TiO2 в роговом слое кожи
Объемная концентр. частиц TiO2:
A.П. Попов и др., Опт. журнал 73, 67-71 (2006).
профиль распределения частиц по глубине

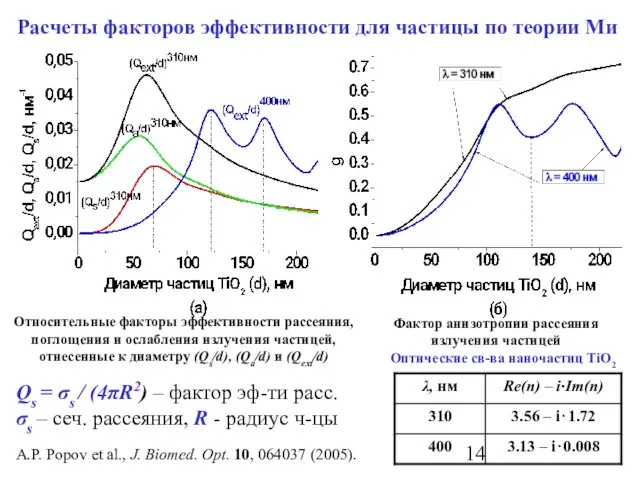
Расчеты факторов эффективности для частицы по теории Ми
Относительные факторы эффективности рассеяния,
поглощения и ослабления излучения частицей,
отнесенные к диаметру (Qs/d), (Qa/d) и (Qext/d)
Фактор анизотропии рассеяния излучения частицей
A.P. Popov et al., J. Biomed. Opt. 10, 064037 (2005).
Qs = σs / (4πR2) – фактор эф-ти расс.
σs – сеч. рассеяния, R - радиус ч-цы
Оптические св-ва наночастиц TiO2

воздух
эпидермис
Параметры рогового слоя
Модель рогового слоя кожи с наночастицами
наночастицы TiO2 в слое, C = 1%
В.В. Тучин 1998.
A = μs(1)/(μs(1) +μsm)
- коэффициент рассеяния частиц
- коэффициент поглощения частиц
- гибридная фазовая функция
- фаз. функция рог. слоя
- коэффициент рассеяния
- коэффициент поглощения
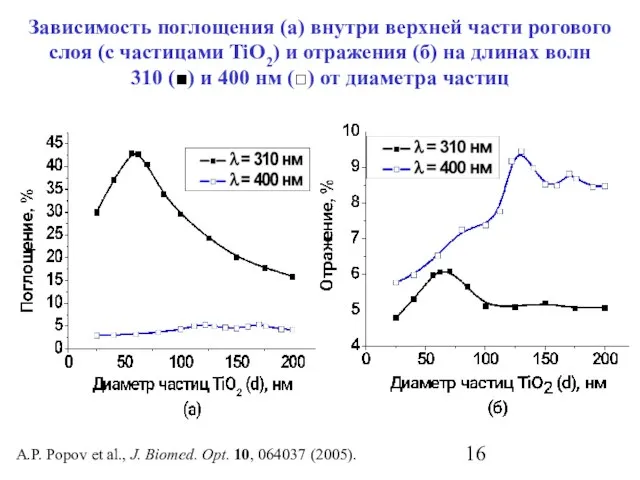
M.W. Ribarsky 1985.

A.P. Popov et al., J. Biomed. Opt. 10, 064037 (2005).
Зависимость поглощения (а) внутри верхней части рогового слоя (с частицами TiO2) и отражения (б) на длинах волн
310 (■) и 400 нм (□) от диаметра частиц

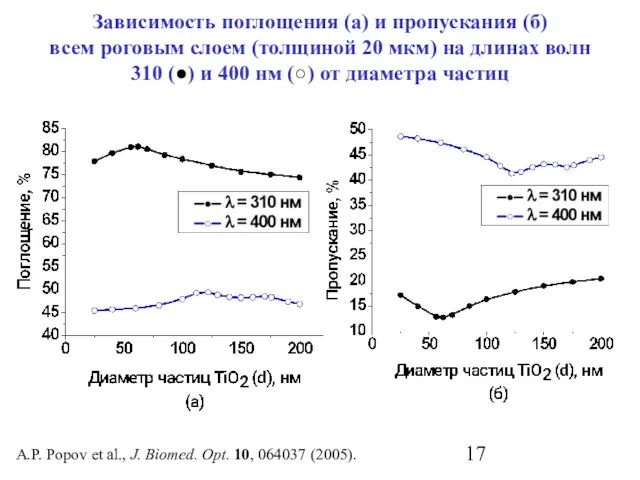
Зависимость поглощения (а) и пропускания (б)
всем роговым слоем (толщиной 20 мкм) на длинах волн
310 (●) и 400 нм (○) от диаметра частиц
A.P. Popov et al., J. Biomed. Opt. 10, 064037 (2005).

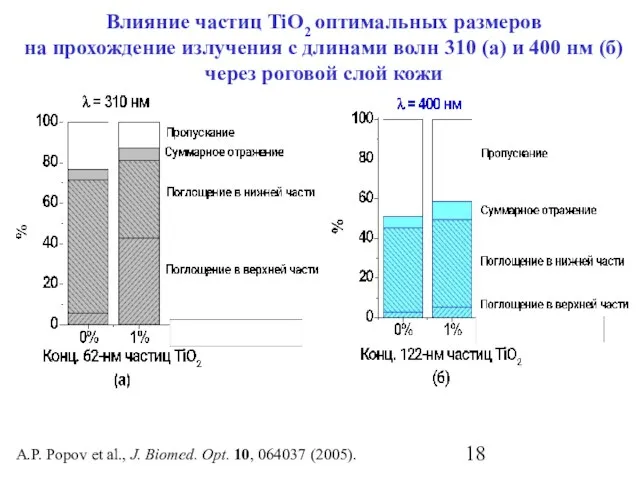
A.P. Popov et al., J. Biomed. Opt. 10, 064037 (2005).
Влияние частиц TiO2 оптимальных размеров
на прохождение излучения с длинами волн 310 (а) и 400 нм (б)
через роговой слой кожи

ЗАЩИЩАЕМЫЕ ПОЛОЖЕНИЯ
1. Сверхкороткие лазерные импульсы (0.1 – 0.5 пс) являются
эффективным инструментом диагностики изменения таких параметров
сильнорассеивающей среды, как коэффициент рассеяния, параметр
анизотропии рассеяния и показатель преломления, имитирующих
cодержание глюкозы в коже в физиологическом диапазоне концентраций
(0 – 500 мг/дл). При этом наиболее чувствительным параметром лазерного
импульса являются его энергия при детектировании излучения,
рассеянного в заднее полупространство.
2. Определен размер наночастиц, наиболее эффективно ослабляющих
оптическое излучение при его распространении в сильнорассеивающей
среде. Он зависит от длины волны излучения и соответствует положению
максимума зависимости фактора экстинкции, отнесенного к диаметру
наночастицы, от ее размера.
3. Основной вклад в ослабление излучения УФ-диапазона в сильнорас-
сеивающей среде толщиной 20 мкм, моделирующий роговой слой кожи,
вносит поглощение, при равномерном распределении наночастиц
диоксида титана размером 25-200 нм с объемной концентрацией
1% в приповерхностном слое толщиной 1 мкм.