La concurrence pure et parfaite

Thèmes abordés
La maximisation des profits à CT
Le seuil de rentabilité
Le seuil de fermeture
L’offre d’une firme en CPP
Équilibre de LT
La CCP et l’efficacité
Exemples

1. Qu’est-ce qu’un marché en CPP?
Un marché en concurrence pure et
parfaite respecte les hypothèses suivantes:
1. Atomicité:
Un grand nombre d'acheteurs et de vendeurs, tous de petite taille par rapport à la taille du marché. Aucun vendeur ni acheteur ne peut influencer le prix de vente par une action individuelle.
2. Homogénéité:
Le produit vendu est homogène (non différencié). Les biens offerts par l’ensemble des firmes en présence sont de parfaits substituts. L'acheteur est indifférent quant au choix du vendeur.

3. Fluidité:
Mobilité complète de tous les facteurs de production (absence de barrières à l'entrée ou à la sortie). De nouvelles firmes peuvent entrer sur le marché si elles identifient la possibilité de réaliser des profits économiques. Elles peuvent également en sortir si elles enregistrent des pertes économiques.
4. Transparence:
Information complète et parfaite. Les consommateurs connaissent les caractéristiques et les prix de tous les produits sur le marché.
Exemples : Certains marchés agricoles, les marchés boursiers, les marchés monétaires internationaux

2. Implications des hypothèses de CPP
Aucun vendeur ni acheteur ne peut influencer le
prix de vente par une action individuelle.
Le prix de vente est donc déterminé par l’interaction de la totalité des offreurs et des demandeurs sur le marché.
↓
La firme est «price-taker»
↓
La firme peut vendre n’importe quelle
quantité au prix du marché.
Par contre, elle ne vendra rien si elle exige
un prix supérieur au prix du marché
↓
La demande à la firme est parfaitement élastique

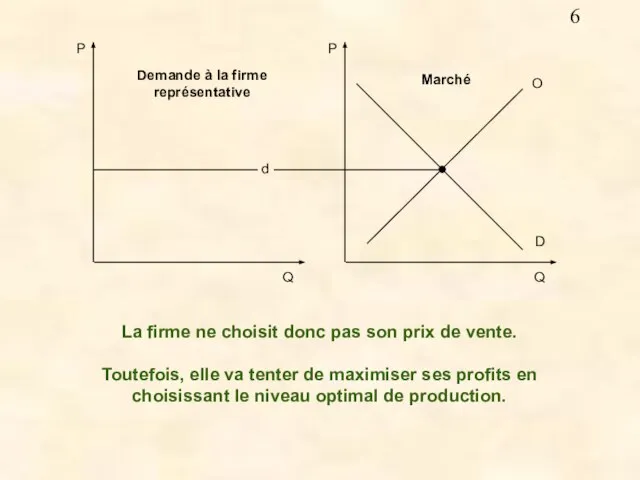
La firme ne choisit donc pas son prix de vente.
Toutefois, elle va tenter de maximiser ses profits en choisissant le niveau optimal de production.

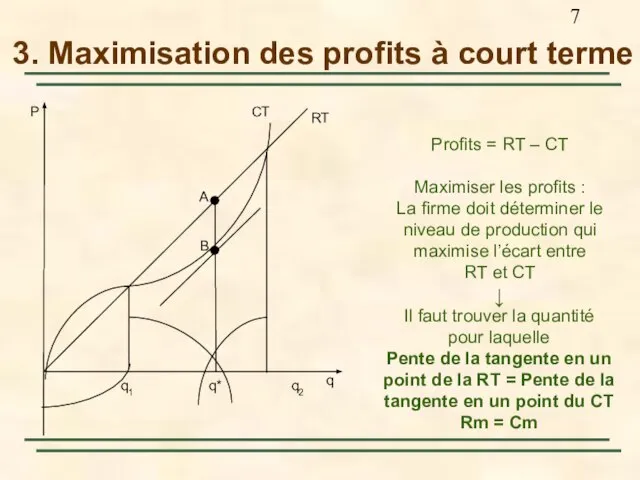
3. Maximisation des profits à court terme
Profits = RT – CT
Maximiser les profits :
La firme doit déterminer le niveau de production qui maximise l’écart entre
RT et CT
↓
Il faut trouver la quantité
pour laquelle
Pente de la tangente en un point de la RT = Pente de la tangente en un point du CT
Rm = Cm

4. Choisir le niveau de production
En concurrence pure et parfaite
RT = P * Q
RM = (P*Q)/Q
RM = P
Rm = dRT/dQ
Rm = d(PQ)/dQ avec P constant
Rm = P
Ou encore, nous savons que :
Comme la demande à la firme est
parfaitement élastique (Ep = ∞), alors Rm = P
1
Rm = P ( 1 - ------ )
│Ep│

Choisir le niveau de production (suite)
Nous avions posé que la règle générale pour qu’une entreprise maximise ses profits est Rm = Cm
Comme dans le cas particulier de la CPP Rm = P
alors la règle de maximisation des profits devient
P = Cm
La firme doit donc choisir le niveau de production qui respecte P=Cm

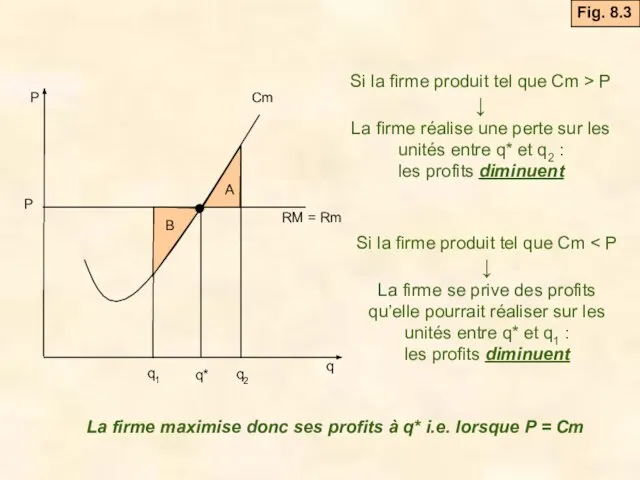
Si la firme produit tel que Cm > P
↓
La firme réalise une perte sur les unités entre q* et q2 :
les profits diminuent
Si la firme produit tel que Cm < P
↓
La firme se prive des profits qu’elle pourrait réaliser sur les unités entre q* et q1 :
les profits diminuent
La firme maximise donc ses profits à q* i.e. lorsque P = Cm
Fig. 8.3

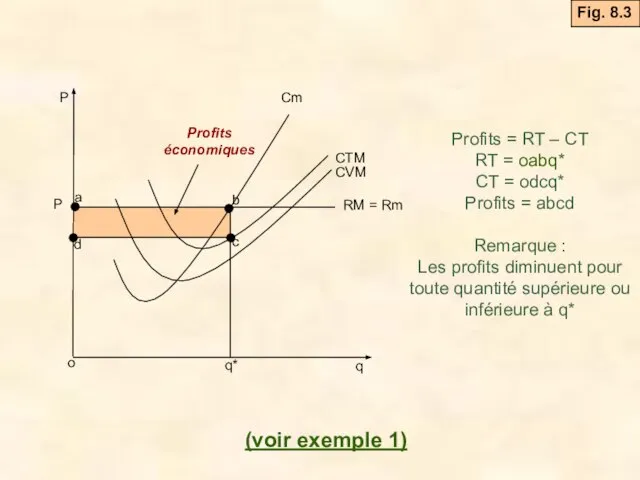
Profits = RT – CT
RT = oabq*
CT = odcq*
Profits = abcd
Remarque :
Les profits diminuent pour toute quantité supérieure ou inférieure à q*
(voir exemple 1)
Fig. 8.3

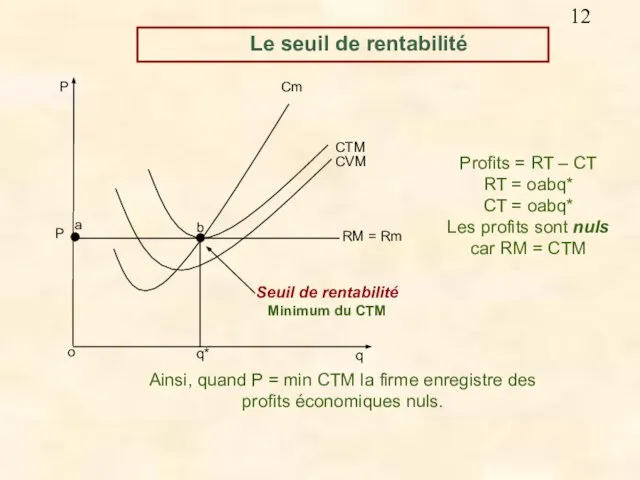
Profits = RT – CT
RT = oabq*
CT = oabq*
Les profits sont nuls
car RM = CTM
Le seuil de rentabilité
Ainsi, quand P = min CTM la firme enregistre des profits économiques nuls.

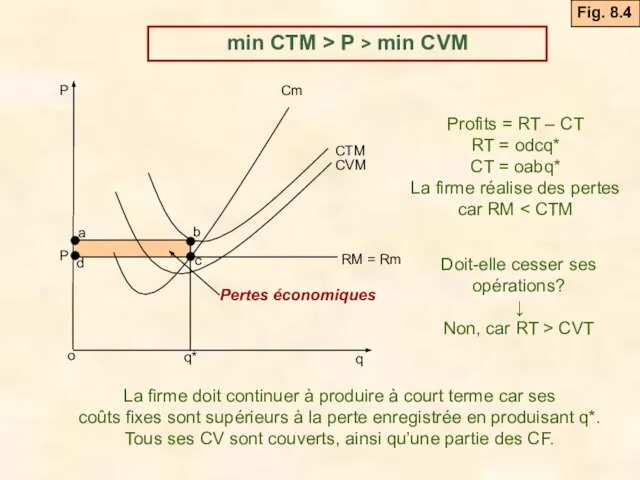
Profits = RT – CT
RT = odcq*
CT = oabq*
La firme réalise des pertes
car RM < CTM
min CTM > P > min CVM
La firme doit continuer à produire à court terme car ses
coûts fixes sont supérieurs à la perte enregistrée en produisant q*.
Tous ses CV sont couverts, ainsi qu’une partie des CF.
Doit-elle cesser ses opérations?
↓
Non, car RT > CVT
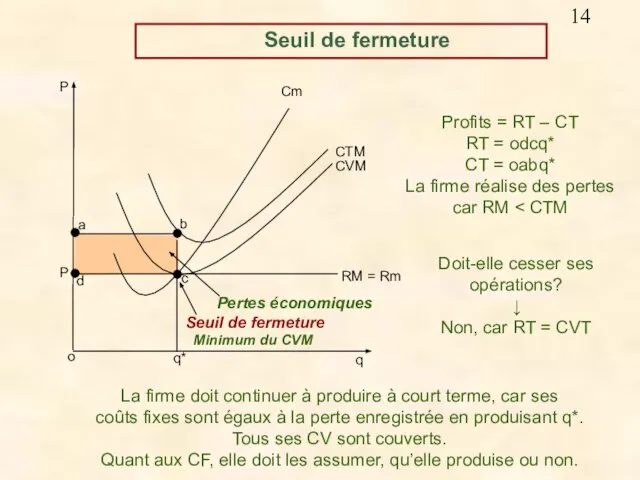
Fig. 8.4

Profits = RT – CT
RT = odcq*
CT = oabq*
La firme réalise des pertes
car RM < CTM
Seuil de fermeture
Doit-elle cesser ses opérations?
↓
Non, car RT = CVT
La firme doit continuer à produire à court terme, car ses
coûts fixes sont égaux à la perte enregistrée en produisant q*.
Tous ses CV sont couverts.
Quant aux CF, elle doit les assumer, qu’elle produise ou non.

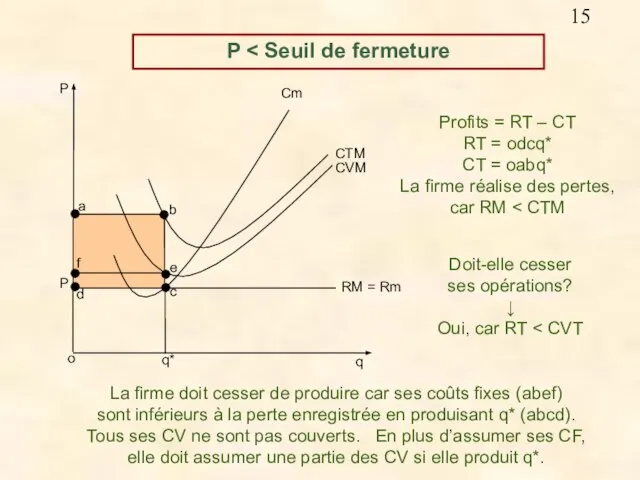
Profits = RT – CT
RT = odcq*
CT = oabq*
La firme réalise des pertes,
car RM < CTM
P < Seuil de fermeture
Doit-elle cesser ses opérations?
↓
Oui, car RT < CVT
La firme doit cesser de produire car ses coûts fixes (abef)
sont inférieurs à la perte enregistrée en produisant q* (abcd).
Tous ses CV ne sont pas couverts. En plus d’assumer ses CF,
elle doit assumer une partie des CV si elle produit q*.

En résumé
Quand le prix du marché (et donc la demande à la firme) diminue, la firme qui veut maximiser ses profits doit réduire sa production.
Si P < min CVM → La firme ne doit pas produire, car elle doit assumer (S de F) les CF et une partie des CV
Si P = min CVM → La firme doit produire. Elle couvre les CV, mais pas (SdeF) les CF. Comme elle doit assumer les CF de toute manière, il est préférable de continuer à produire à court terme. (S de F))
Si min CTM > P > min CVM → La firme doit produire, car elle couvre ses (S de R) (S de F) CV et une partie des CF.
Si P = min CTM → Les profits économiques sont nuls (S de R)
(S de R)
Si P > min CTM → La firme réalise des profits économiques positifs.
(S de R)
(voir exemple 2)

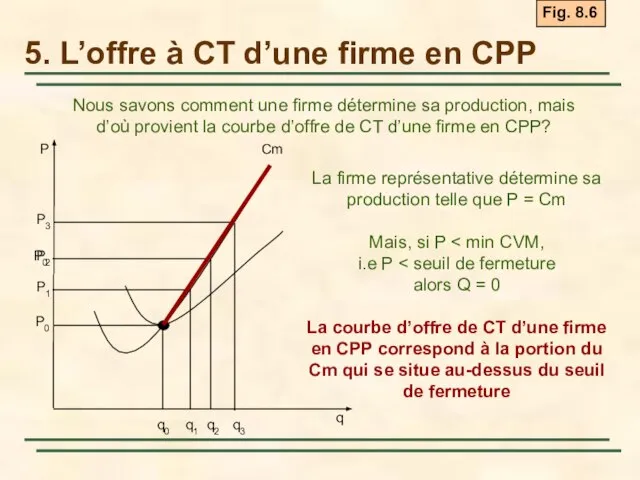
5. L’offre à CT d’une firme en CPP
Nous savons comment une firme détermine sa production, mais
d’où provient la courbe d’offre de CT d’une firme en CPP?
La firme représentative détermine sa production telle que P = Cm
Mais, si P < min CVM,
i.e P < seuil de fermeture
alors Q = 0
La courbe d’offre de CT d’une firme en CPP correspond à la portion du Cm qui se situe au-dessus du seuil de fermeture
Fig. 8.6

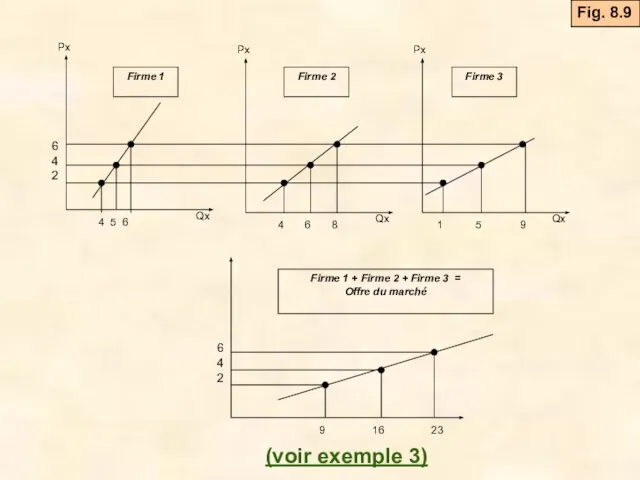
6. L’offre à CT du marché
L’offre du marché représente la quantité totale qui sera produite par l’ensemble des firmes à chaque niveau de prix.
Puisque la quantité offerte par chaque firme est déterminée par la portion du Cm au-dessus du min du CVM, la somme horizontale des Cm (au-dessus du min du CVM) de toutes les firmes va donc déterminer la production réalisée par l’ensemble des firmes
Il s’agit donc de faire la somme des quantités offertes (somme sur Q) pour toutes les firmes individuelles pour chaque niveau de prix.

Fig. 8.9
(voir exemple 3)

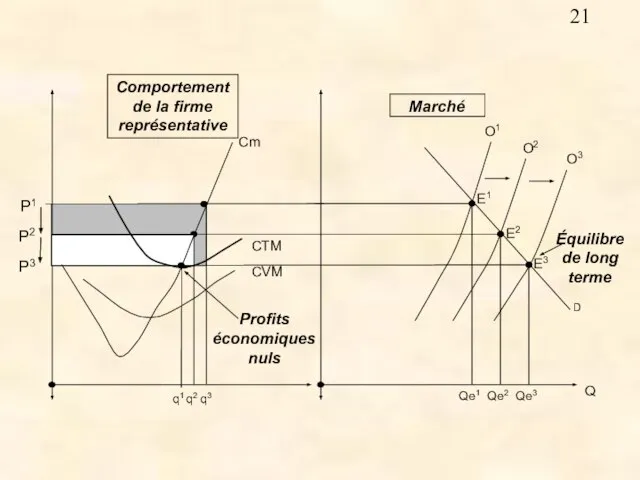
7. L’équilibre de long terme
Une hypothèse importante de la CPP : Fluidité
Si la firme réalise des profits à CT : (1) entrée de nouvelles firmes sur le marché et (2) les firmes déjà existantes produiront davantage
↓
Hausse de l’offre du marché
↓
Baisse du prix d’équilibre
↓
Baisse de la demande à la firme représentative
↓
Baisse des profits de la firme représentative
↓
Le processus se poursuit jusqu’au moment où plus aucune firme n’est incitée à entrer sur le marché, i.e. lorsque les profits économiques sont nuls

En résumé
Il y a entrée de nouvelles firmes tant qu’il y a des
profits économiques
Il y a sortie de firmes tant qu’il y a des pertes économiques
Les firmes cessent d’entrer et de sortir du marché dès que les profits économiques sont nuls.
À long terme, en CPP :
- les profits économiques sont nuls
- P = min du CM
- Les consommateurs paient le plus bas prix possible
(voir exemple 4)

8. La CPP est-elle efficace?
En CPP, un marché se trouve à l’équilibre: P = P* et Q = Q*
Cette situation permet-elle
d’éviter le gaspillage?
d’utiliser les ressources de la meilleure manière possible?
d’amener l’ensemble de la société au plus haut niveau de satisfaction étant donné les ressources disponibles?

Le surplus du producteur
Chaque point le long de la fonction d’offre représente le prix minimum exigé par le producteur pour chaque unité produite.
↓
Le surplus du producteur est la différence entre le prix obtenu par le producteur sur le marché et le prix minimum qu’il aurait exigé pour chacune des unités vendues.
↓
Graphiquement, il est représenté par toute la surface au-dessus de l’offre et au-dessous du prix.
↓
Le surplus du producteur est une mesure du bien-être des producteurs, et non une mesure des profits.

Surplus du producteur :
[(10-1) * 100] /2 = 450 $
Remarque : toute hausse du prix, ceteris paribus, fait augmenter le surplus du producteur, toute baisse le fait diminuer.

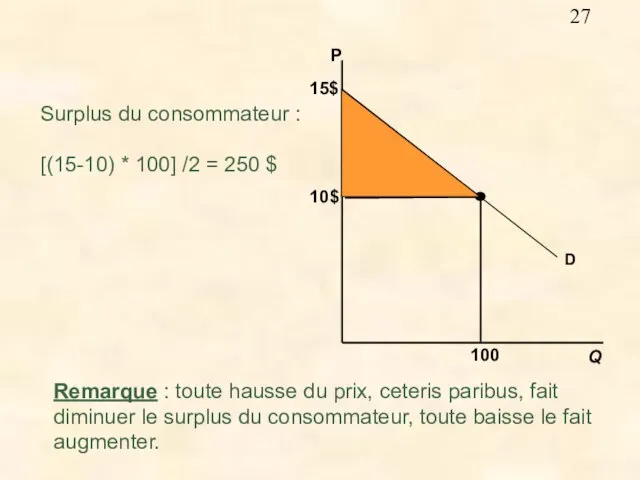
Le surplus du consommateur
Chaque point le long de la fonction de demande représente le prix maximum que les consommateurs sont prêts à payer pour chaque unité produite (volonté de payer).
↓
Le surplus du consommateur est la différence entre la volonté de payer du consommateur et le prix payé
↓
Graphiquement, il est représenté par toute la surface au-dessous de la demande et au-dessus du prix.
↓
Le surplus du consommateur est une mesure du bien-être des consommateurs.

Remarque : toute hausse du prix, ceteris paribus, fait diminuer le surplus du consommateur, toute baisse le fait augmenter.
Surplus du consommateur :
[(15-10) * 100] /2 = 250 $

Le bien-être collectif
(le surplus total)
P
Bien-être collectif = SC + SP
Lorsque le marché est efficace, le BEC est maximisé uniquement pour la combinaison prix/quantité d’équilibre. Toute autre combinaison réduit le BEC
(voir exemple 5)

Exemples

Exemple 1
La fonction de coût total d’une firme est donnée par l’équation suivante: CT = 10 + 2Q2
Si la firme évolue dans un contexte de CPP et que toutes les autres firmes sur le marché affichent un prix de 20$
Quel prix la firme devrait-elle exiger?
Quelle quantité devrait-elle produire afin de maximiser ses profits?
3) Quels seront ses profits?

Réponses :
En CPP, la firme ne peut pas choisir son prix. Elle doit adopter le prix du marché, soit 20$.
2) Règle de maximisation des profits : P = Cm
Cm = dCT/dQ = 4Q
Donc les profits sont maximisés si 20 = 4Q, donc Q = 5
3) Profits = RT – CT
Profits = (5*20) – [10 + 2(5)2]
Profits = 100 – 60
Profits = 40

Exemple 2
La fonction de coût total d’une firme est donnée par l’équation suivante: CT = 250 + Q2
Si la firme évolue dans un contexte de CPP et que toutes les autres firmes sur le marché affichent un prix de 10$
Quelle quantité devrait-elle produire afin de maximiser ses profits ou de minimiser ses pertes?
2) Quels seront ses profits ou ses pertes si la firme prend une décision optimale?

Réponses:
1) Règle de maximisation des profits : P = Cm
Cm = dCT/dQ = 2Q. Donc les profits sont maximisés si 10 = 2Q, donc Q* = 5
CFT = 250 et CVT= Q2
CVM = CVT/Q = Q2/Q = Q
Si Q = 5, alors CVM = 5
Puisque P > CVM, la firme a intérêt à produire 5 unités
Profits = RT – CT = 50 - [250 + 52] → Pertes = 225
La décision optimale de la firme est de produire 5 unités même si elle doit assumer des pertes car, les pertes avec production (225$) sont inférieures aux CF à assumer (250$) si elle cesse sa production.

Exemple 3
Un marché est composé de trois firmes dont les fonctions d’offre sont les suivantes :
QO1 = 12 + 4P
QO2 = 17 + 5P
QO3 = 20 + 8p
Quelle est la fonction d’offre du marché?
Réponses :
L’offre de marché est la somme sur les quantités des offres individuelles.
Qo = QO1 + QO2 + QO3 = 49 + 17P

Exemple 4
Alain Crevable inc. est une firme familiale spécialisée dans la réparation de pneus de tous genres.
Les fonctions de demande et d’offre du marché sont les suivantes :
Qd = 480 – 2P
Qo = 160 + 3P
La fonction de coût total de la firme est la suivante :
CT = 12 + 8q +4q2
1) Trouver le prix et la quantité d’équilibre du marché.
Quelle quantité produira la firme représentative en supposant qu’elle souhaite maximiser ses profits?
Combien de firmes cette industrie compte-t-elle?
Trouver les seuils de rentabilité et de fermeture
Quels sont les profits réalisés par la firme représentative?
Comment le marché s’ajustera-t-il à long terme? Combien y aura-t-il de firmes?

Réponses :
P* = 64$ Q* = 352
P = Cm
64 = 8 + 8q
q* = 7
352/7 = 50,3 firmes
Seuil de rentabilité
Cm = CTM
8 + 8q = (12+8q+4q2)/q
q = √3 → q = 1,73
P = Cm
P = 8 + 8(1,73)
P = 21,8$
Seuil de fermeture
Cm = CVM
8 + 8q = 8 + 4q
q = 0
P = Cm
P = 8 + 8(0)
P = 8$
5) Profits = RT – CT
Profits = (64*7) – [12 + 8(7) + 4(7)2]
Profits = 184

Les profits économiques sont positifs. Il y aura donc entrée de nouvelles firmes sur le marché. À long terme, le prix du marché se fixera au seuil de rentabilité (21,8$) et les profits économiques seront nuls.
Avec P = 21,8$
Qd = 480 – 2(21,8) = 436,4
Puisqu’à LT chaque firme produit 1,73 unité, il y aura 252,2 firmes sur le marché (436,4/1,73).

Exemple 5
Qd = 2000 –0,5P Qo = -400 + P
a) Trouver le prix et la quantité d’équilibre.
b) Calculer les surplus du consommateur et du producteur
c) Supposons un contrôle de prix à 1200$. Calculer les surplus du consommateur et du producteur
Réponses :
a) Qd = Qo
2000 – 0,5P = -400 + P
2400 = 1,5P → P* = 1600 Q* = 1200

b) SC = [(4000 – 1600) * 1200] / 2 = 1 440 000 = SC
SP = [(1600 – 400) * 1200] / 2 = 720 000 = SP
BEC = SC + SP = 2 160 000

c) Qd = 2000 – 0,5P
= 2000 – 0,5 (1200) = 1400 = Qd
Qo = -400 + P
= – 400 + 1200 = 800 = Qo
Qd > Qo = Pénurie = 600
Quelle est la valeur que les consommateurs accordent à la 800ième unités? 800 = 2000 – 0,5P → P = 2400
SC = A + B + D
= [(4000-2400)*800]/2 + (2400 –1200)*800 = 1 600 000 = SC
SP = F
= [(1200 – 400) * 800] / 2 = 320 000 = SP
BEC = SC + SP = 1 920 000