Содержание
- 2. Множество – это объект, образованный за счет мысленного собирания в единое целое каких-либо предметов, в том
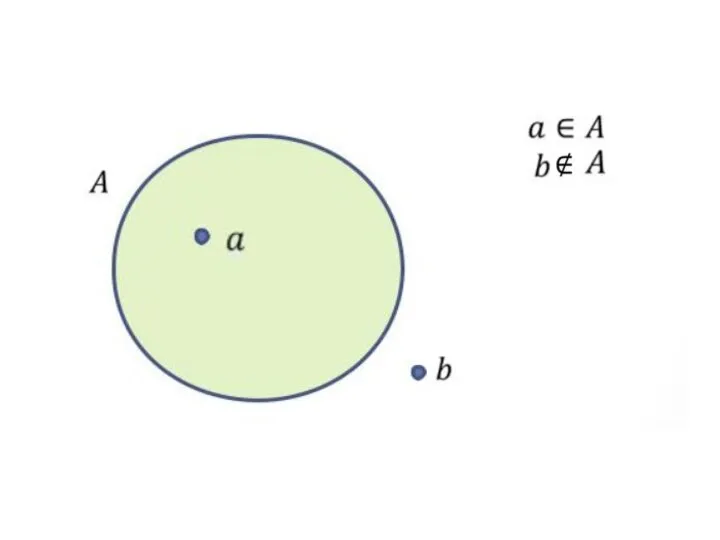
- 3. Пустое множество не содержит ни одного элемента и обозначается ø . Запись означает, что элемент принадлежит
- 5. Множества бывают конечные и бесконечные. Примеры: 1) множество жителей г. Москвы конечное; 2) множество натуральных чисел
- 6. Задание множеств осуществляется несколькими способами Если множество содержит конечное число элементов и легко обозримо, оно может
- 7. 2. Множество может быть задано аналитически – посредством некоторого признака, присущего всем его и только его
- 8. 3. Множество может быть задано алгоритмически – некоторым алгоритмом, порождающим из одних элементов множества другие его
- 9. Другой пример алгоритмического задания множества. Пусть M = {1, 2, 4, 8, 16,…} — множество степеней
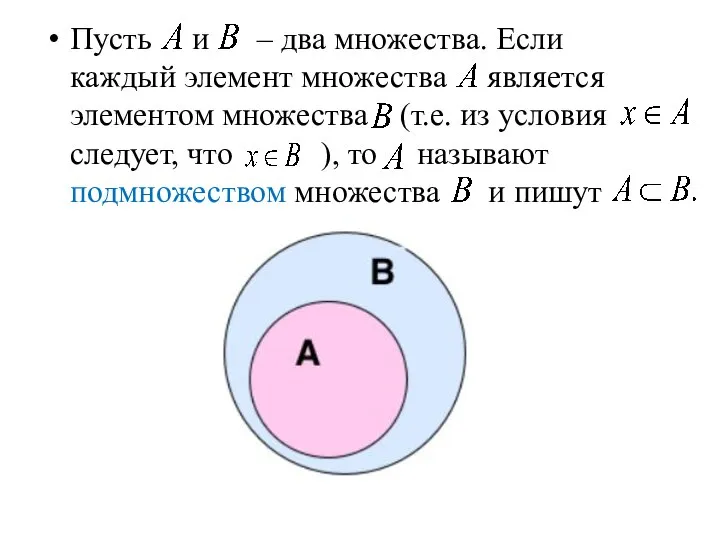
- 10. Пусть и – два множества. Если каждый элемент множества является элементом множества (т.е. из условия следует,
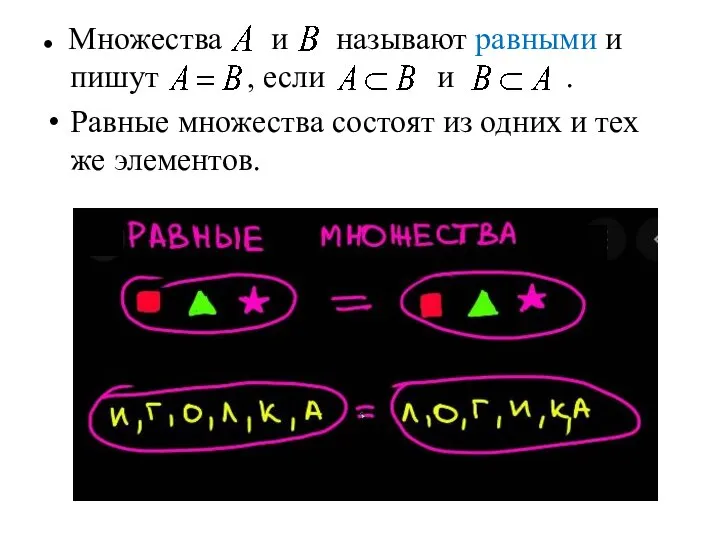
- 11. ● Множества и называют равными и пишут , если и . Равные множества состоят из одних
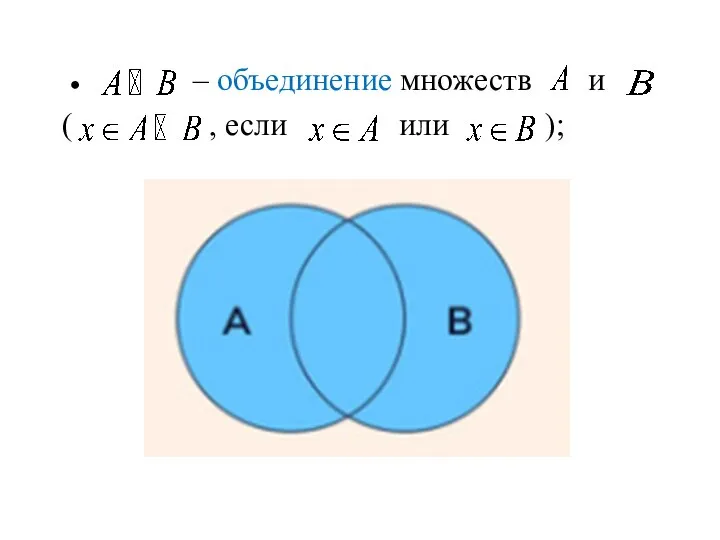
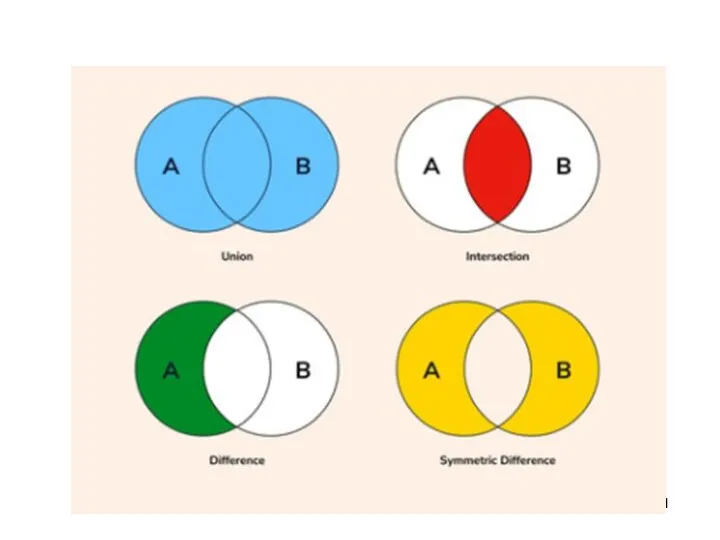
- 12. ● – объединение множеств и ( , если или );
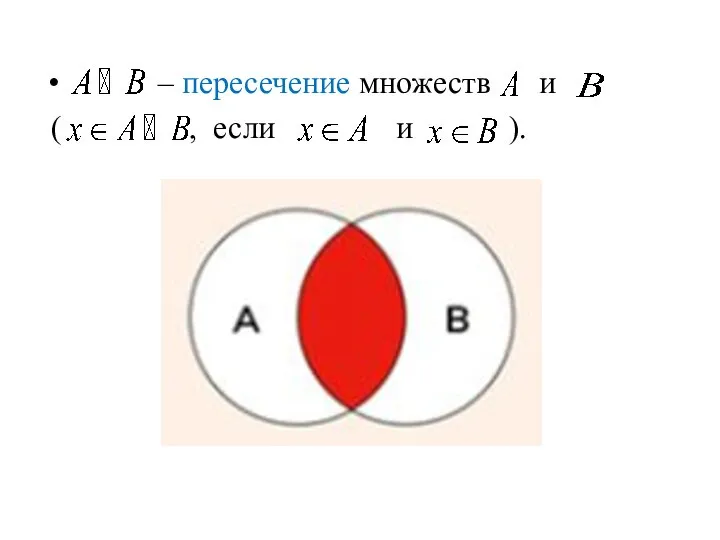
- 13. – пересечение множеств и ( , если и ).
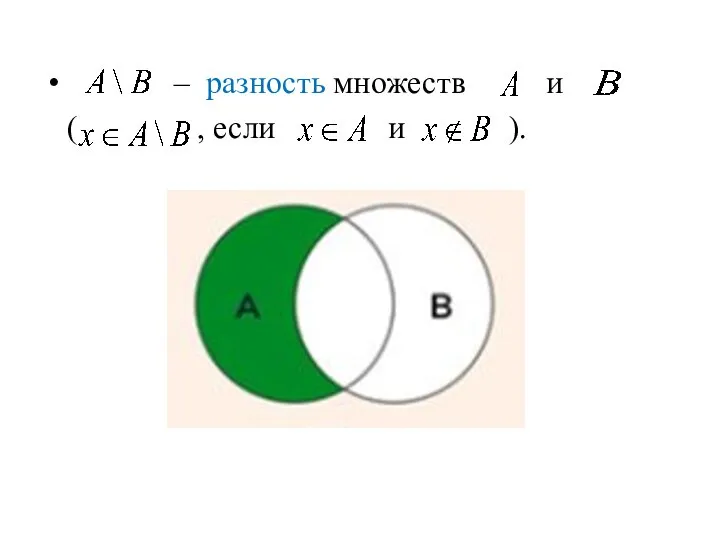
- 14. – разность множеств и ( , если и ).
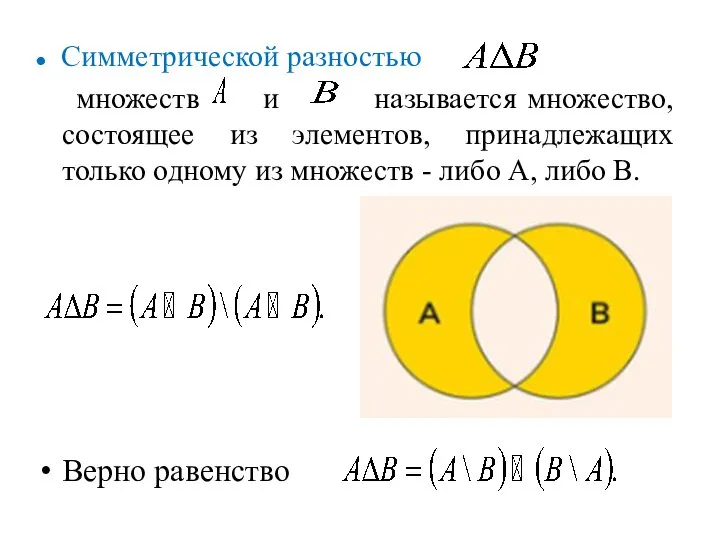
- 15. ● Симметрической разностью множеств и называется множество, состоящее из элементов, принадлежащих только одному из множеств -
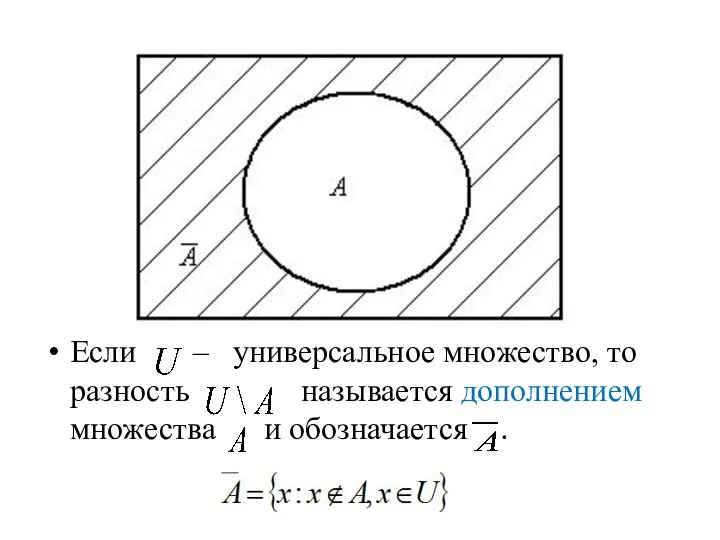
- 17. Если – универсальное множество, то разность называется дополнением множества и обозначается .
- 18. Декартово произведение множеств и обозначается и состоит из всех упорядоченных пар таких, что и . Таким
- 19. Пример 1. Даны множества Найдите Решение. Вопрос:
- 21. Правило умножения Если элемент x можно выбрать m способами, а элемент y можно выбрать n способами,
- 22. Правило сложения Число элементов множества находится по формуле В частности, если множества А и В не
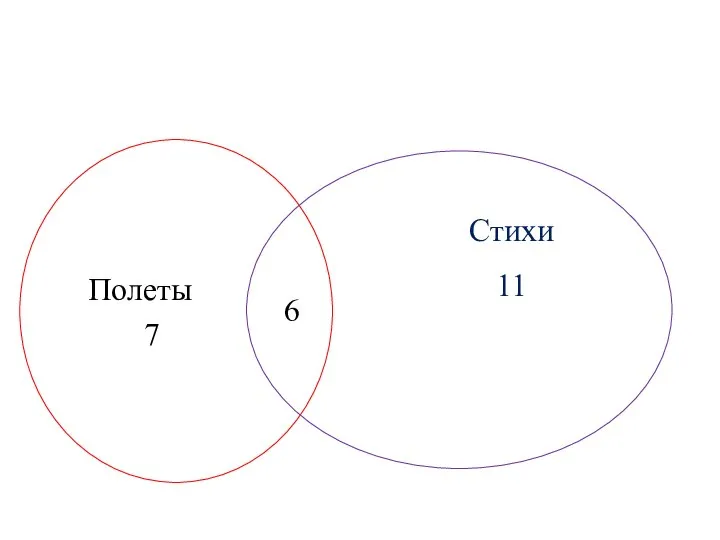
- 23. Пример 2. В группе из 27 студентов 17 пишут стихи, а 13 летают во сне. Трое
- 24. Полеты 7 Стихи 11 6
- 25. Пример 3. Из 50 студентов курса 42 изучают английский язык, 31 – немецкий язык, а 25
- 26. 1 способ. 1) Найдем число элементов в объединении данных множеств. Для этого воспользуемся формулой правила сложения:
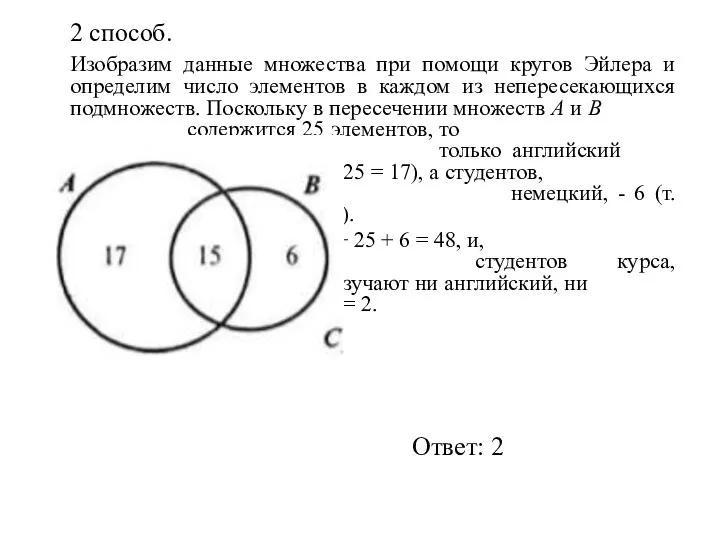
- 27. 2 способ. Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из
- 29. Скачать презентацию








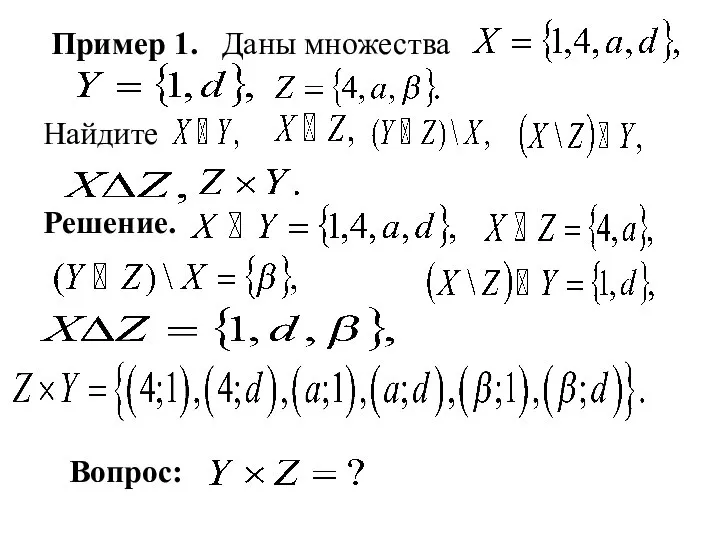






 Строение Живого организма
Строение Живого организма Отчет_Восприятие готовой еды и марки LAVKALAVKA_08.09_с дегустацией
Отчет_Восприятие готовой еды и марки LAVKALAVKA_08.09_с дегустацией Теоретические основы электротехники
Теоретические основы электротехники Право. Тема 2. Государство и право. Их роль в жизни общества
Право. Тема 2. Государство и право. Их роль в жизни общества Читательская конференция
Читательская конференция кроссворды на английском языке
кроссворды на английском языке Презентация на тему Мои домашние животные (1 класс)
Презентация на тему Мои домашние животные (1 класс) Чисто прогестиновые инъекционные контрацептивы (ЧПИК)
Чисто прогестиновые инъекционные контрацептивы (ЧПИК) Презентацию подготовил
Презентацию подготовил Тема: «Творительный и предложный падежи имен прилагательных мужского и среднего рода.»
Тема: «Творительный и предложный падежи имен прилагательных мужского и среднего рода.» О природе конфликта
О природе конфликта Участник конкурса Студент года
Участник конкурса Студент года Public.Ru
Public.Ru Занимательные задачи (5 класс)
Занимательные задачи (5 класс) Вебинар 1. IMM
Вебинар 1. IMM Вопросительные местоимения
Вопросительные местоимения Презентация на тему:Элементы Комбинаторики!!!
Презентация на тему:Элементы Комбинаторики!!! «Компьютер: польза или вред».
«Компьютер: польза или вред». Техника безопасности на занятиях гимнастики. Основные группы мышц и способы их развития
Техника безопасности на занятиях гимнастики. Основные группы мышц и способы их развития Заграничный поход русской армии. Внешняя политика в 1813-1825 гг.
Заграничный поход русской армии. Внешняя политика в 1813-1825 гг. Итоги фотоконкурса Studmirror
Итоги фотоконкурса Studmirror Презентация на тему О числах
Презентация на тему О числах Бесплатная виртуализация Citrix XenServer для компаний
Бесплатная виртуализация Citrix XenServer для компаний Семинар по проблеме:«Организация внеурочной деятельности по ФГОС в начальной школе».
Семинар по проблеме:«Организация внеурочной деятельности по ФГОС в начальной школе». Заселение Дальнего Востока России
Заселение Дальнего Востока России Общие сведения о глаголе. Спряжения латинского глагола. Занятие 8
Общие сведения о глаголе. Спряжения латинского глагола. Занятие 8 Архитектор Пути Клиента
Архитектор Пути Клиента Color expressions
Color expressions