Содержание
- 2. Summary of Previous Lecture What is logic The difference between rhetoric and logic Difference between a
- 3. TODAY’S PLAN History of Categorical Logic What is Categorical Logic? Elements of Categorical Logic Quantity Quality
- 4. Historical Overview (Aristotle and the Stoics) Aristotle forefather of Modern Logic Aristotelian Logic is known as
- 5. Aristotle’s work on Logic is rich and complex - Included in the Organon Consists of several
- 6. Aristotelian Logic is based on Deductive Reasoning AND that is grounded on two ideas/notions or pillars:
- 7. BIG ISSUE: Underlying Aristotle’s magnificent work in Logic there is a deep question IS LOGIC PART
- 8. 2. What is Categorical Logic? A fairly simple logic of categories or classes In this logic,
- 9. In categorical logic, important logical terms are the terms “all” and “some.” In categorical logic we
- 10. Categorical logic is the logic that deals with the logical relationship between categorical propositions. A categorical
- 11. EXAMPLE: DOGS ARE ANIMALS (every categorical proposition has two terms) TWO CATEGORIES/CLASSES HERE DOGS subject term
- 12. How the first category relates to the second, helpful means to compare classes DOGS ARE ANIMALS….
- 13. MEN ARE MAMMALS…. (ALL) MEN ARE MAMMALS 17
- 14. CATEGORICAL PROPOSITIONS essentially explain the relationship between two categories whether or not –for instance- they need
- 15. ARE (verbs in general) = COPULA (element that glues predicate and subject term together) Yet, We
- 16. FOUR BASIC ELEMENTS IN CATEGORICAL LOGIC SUBJECT TERM PREDICATE TERM COPULA QUANTIFIERS 20
- 17. QUICK EXERCISE –individuate subject term, predicate term, copula and quantifier All mice are rodents. Some basketball
- 18. Since, categorical logic asserts that either all or parts of a class denoted by the subject
- 19. The QUANTITY of a proposition is either universal or particular. A proposition is UNIVERSAL if its
- 20. All S are P 2. No S are P 3. Some S are P 4. Some
- 21. 5. Quality – in which way? In what way Are the classes being related? Affirmative –
- 22. The QUALITY of a proposition is either affirmative or negative. A proposition is NEGATIVE if the
- 23. All S are P 2. No S are P 3. Some S are P 4. Some
- 24. FOUR BASIC FORMS 14 Porphyry’s Isagoge b. Boethius’ On the Categorical Syllogism c. Abelard’s Dialectica d.
- 25. Summing up: 15
- 26. EXERCISE Identify the form of the categorical statements expressed by the following sentences. All heroes are
- 27. 6. Distribution 17
- 28. A term in a claim is DISTRIBUTED when it says something definite about all members of
- 29. The A proposition [All S are P] says that every member of the subject class is
- 30. But is reference being made to every member of the predicate class? NO. Example: "All artists
- 31. The E proposition [No S are P] makes reference in a negative way to every member
- 32. In the I proposition [some S are P] the quantifier [some] makes it clear that only
- 33. In the O proposition [Some S are not P] the quantifier "some" shows that the reference
- 34. SUMMARY 24
- 36. Скачать презентацию



























![The A proposition [All S are P] says that every member of](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/930225/slide-28.jpg)

![The E proposition [No S are P] makes reference in a negative](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/930225/slide-30.jpg)
![In the I proposition [some S are P] the quantifier [some] makes](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/930225/slide-31.jpg)
![In the O proposition [Some S are not P] the quantifier "some"](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/930225/slide-32.jpg)
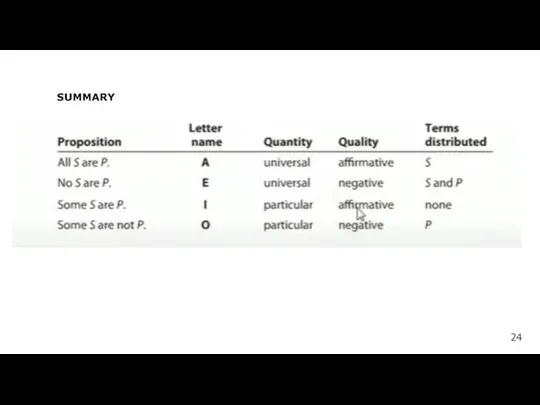
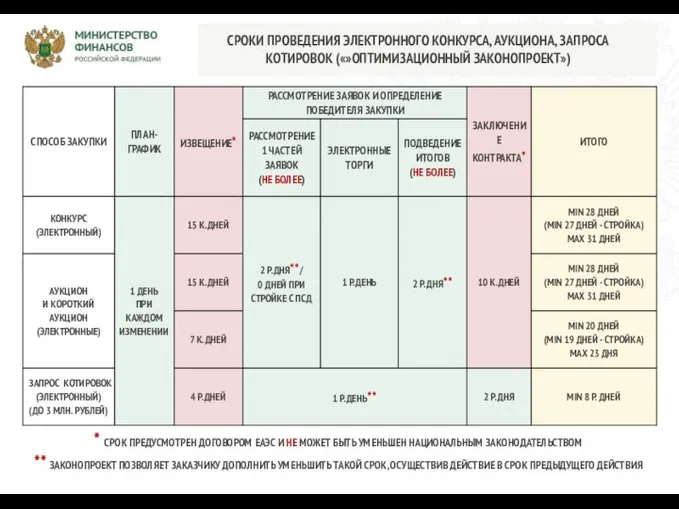 Таблица сроков проведения электронного конкурса, аукциона
Таблица сроков проведения электронного конкурса, аукциона Город Николаев
Город Николаев Противоречат ли социальные цели экономическому развитию и экономическому росту
Противоречат ли социальные цели экономическому развитию и экономическому росту  Мини-лапта
Мини-лапта УСТАНОВЛЕНИЕ ДИАГНОЗА УРОГЕНИТАЛЬНОГО ХЛАМИДИОЗА У ПОЛОВЫХ ПАР
УСТАНОВЛЕНИЕ ДИАГНОЗА УРОГЕНИТАЛЬНОГО ХЛАМИДИОЗА У ПОЛОВЫХ ПАР Презентация на тему Памятные места города-героя Керчи
Презентация на тему Памятные места города-героя Керчи Почему нужно изучать Экологию?
Почему нужно изучать Экологию? Ориентирование на местности (6 класс)
Ориентирование на местности (6 класс)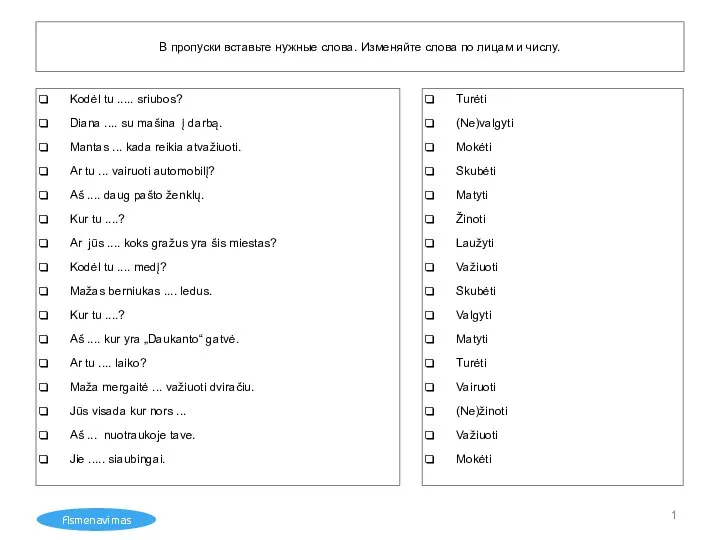 Asmenavimas uzduotys
Asmenavimas uzduotys США 1945 -1970рр
США 1945 -1970рр Исследовательский проектИстория народной медицины
Исследовательский проектИстория народной медицины Международный конкурс “National History
Международный конкурс “National History Технология распиливания кости
Технология распиливания кости Практика в pr-агентстве “Гуров и партнеры”
Практика в pr-агентстве “Гуров и партнеры” РЕН ТВ ПРЕДСТАВЛЯЕТ
РЕН ТВ ПРЕДСТАВЛЯЕТ ОСНОВЫ РЕГИОНАЛЬНОГО ПРОЕКТИВАНИЯ
ОСНОВЫ РЕГИОНАЛЬНОГО ПРОЕКТИВАНИЯ Понятие власти
Понятие власти Административное право
Административное право Фонетика. Графика. Орфография. Орфоэпия
Фонетика. Графика. Орфография. Орфоэпия ВОЛОНТЕРСТВО -
ВОЛОНТЕРСТВО - Стресс-менеджмент руководителя
Стресс-менеджмент руководителя Жестокое обращение с ребенком и его последствия для развития ребенка
Жестокое обращение с ребенком и его последствия для развития ребенка Основы педагогического мастерства
Основы педагогического мастерства Внешняя торговля России
Внешняя торговля России Павильон Азербайджана на ЭКСПО-2015 в Милане
Павильон Азербайджана на ЭКСПО-2015 в Милане Общая психология. Ощущения. Восприятие
Общая психология. Ощущения. Восприятие Ценность фигур. Шахматы в школе
Ценность фигур. Шахматы в школе Презентация на тему Конфликты и пути их разрешения
Презентация на тему Конфликты и пути их разрешения