Лекция 10. Однофакторный дисперсионный анализ

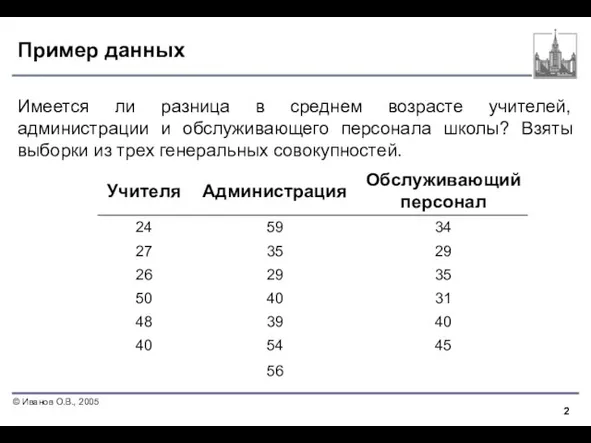
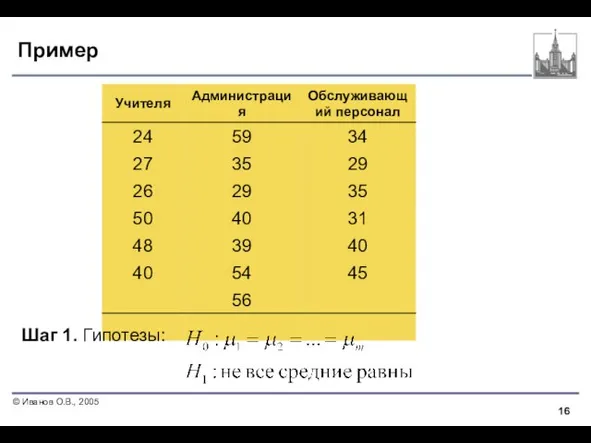
Пример данных
Имеется ли разница в среднем возрасте учителей, администрации и обслуживающего персонала школы? Взяты выборки из трех генеральных совокупностей.

10-1.
Задача дисперсионного анализа
Однофакторный и двухфакторный дисперсионный анализ

Дисперсионный анализ (Analysis of Variance)
F-критерий, который мы использовали при сравнении дисперсий, может применяться для сравнения трех и более средних.
Этот метод называется дисперсионным анализом или в англоязычной аббревиатуре ANOVA (Analysis of Variance).
F-критерий можно использовать при сравнении двух средних. Но в этом случае он становится идентичным t-критерию.

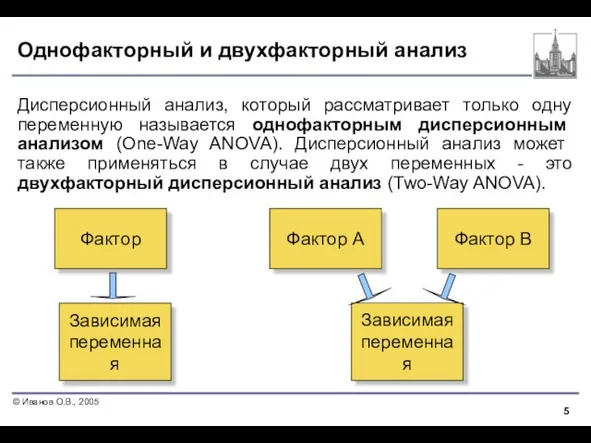
Однофакторный и двухфакторный анализ
Дисперсионный анализ, который рассматривает только одну переменную называется однофакторным дисперсионным анализом (One-Way ANOVA). Дисперсионный анализ может также применяться в случае двух переменных - это двухфакторный дисперсионный анализ (Two-Way ANOVA).
Фактор А
Фактор B
Зависимая
переменная
Фактор
Зависимая
переменная

10-2.
Однофакторный дисперсионный анализ
Постановка задачи
Описание метода
Пример

Признак, фактор и уровни фактора
Исследуется только один признак или переменная: возраст сотрудников.
Рассматривается только один фактор: категория персонала.
Три уровня фактора: учителя, администрация, обслуживающий персонал.

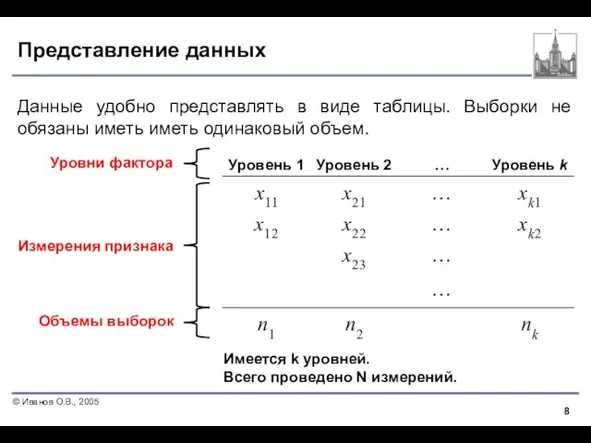
Представление данных
Данные удобно представлять в виде таблицы. Выборки не обязаны иметь иметь одинаковый объем.
Уровни фактора
Измерения признака
Имеется k уровней.
Всего проведено N измерений.
Объемы выборок

Условия применения
1. Генеральные совокупности, из которых формируются выборки, должны быть нормально распределены.
2. Выборки должны быть независимы.
3. Дисперсии генеральных совокупностей должны быть равны.

Гипотезы
Для выявления различия между тремя и более средними, выдвигаются следующие гипотезы:
не все средние равны

Метод
Вычисляются две оценки: межгрупповая дисперсия и внутригрупповая дисперсия.
Если нет разницы в средних, то оценки межгрупповой и внутригрупповой дисперсий приблизительно равны и значение F-критерия близко к 1, поэтому нулевая гипотеза принимается.
Если различие в средних значительно, межгрупповая дисперсия будет гораздо больше, чем внутригрупповая. Значение F-критерия будет значительно больше 1 и нулевая гипотеза будет отвергнута.
Поскольку при проверке гипотезы мы сравниваем дисперсии, метод и получил название дисперсионный анализ.

Степени свободы и критическая область
Степени свободы F-распределения задаются двумя значениями:
Числителя: df = k – 1
Знаменателя: df = N – k
Уравнение критической области (правосторонняя):

Суммы квадратов отклонений
Межгрупповая сумма квадратов отклонений:
Внутригрупповая сумма квадратов отклонений:
Общая сумма квадратов отклонений:
Between Groups
Within Groups
Sum Square
Sum Square
Sum Square

Факторная и остаточная дисперсия. Критерий
Межгрупповая (факторная) дисперсия:
Внутригрупповая (остаточная) дисперсия:
F-критерий:
Between Groups
Within Groups
Mean Square
Mean Square

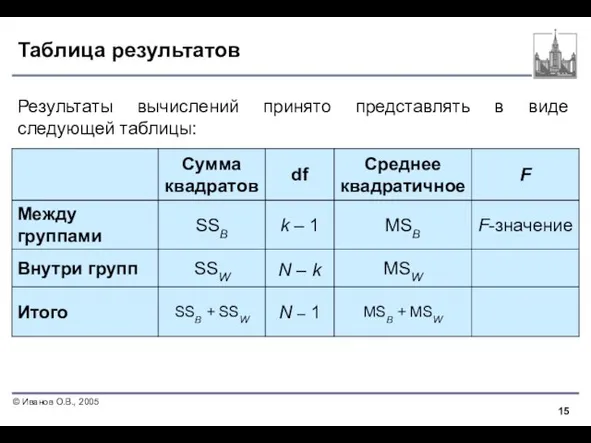
Таблица результатов
Результаты вычислений принято представлять в виде следующей таблицы:

Пример
Шаг 1. Гипотезы:

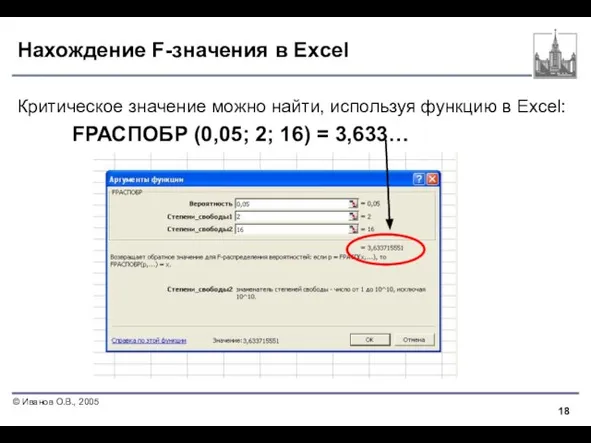
Шаг 2. Критическая область
Найдем критическое значение по таблице критических точек распределения Фишера.
Уровень значимости α = 0,05.
Так как k = 3 и N = 19, то
числитель df = k – 1 = 3 – 1 = 2
знаменатель df = N – k = 19 – 3 = 16
Критическое значение равно 3,633.
Критическая область F > 3,633

Нахождение F-значения в Excel
Критическое значение можно найти, используя функцию в Excel:
FРАСПОБР (0,05; 2; 16) = 3,633…

Шаг 3. Вычисление статистики F
Шаг 3a. Подсчет средних

Шаг 3b. Расчет отклонений

Шаг 3c. Расчет дисперсий

Шаг 3d. Расчет статистики

Шаг 4-5. Получение выводов, ответ
1,649 < 3,633
Полученное значение статистики не попало в критическую область. У нас нет оснований думать, что средние значения отличаются.
Ответ.
Средний возраст рассматриваемых категорий персонала не различается значимо.

10-3.
Решение задачи в SPSS
Ввод данных
Анализ
Отчет