Содержание
- 2. Цель лекции: Изучить спектры периодических и непериодических сигналов План: Ряды Фурье Спектры периодических сигналов Преобразование Фурье
- 3. Ряд Фурье. Спектры периодических сигналов Периодические негармонические функции можно разложить в ряд Фурье. Для этого периодическая
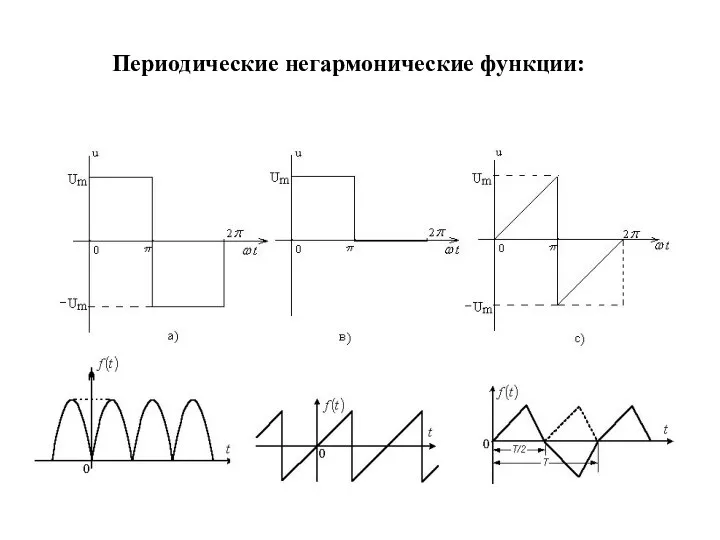
- 4. Периодические негармонические функции:
- 5. Синусно-косинусная форма ряда Фурье:
- 6. - постоянный коэффициент ряда Фурье коэффициенты косинусной составляющей ряда Фурье коэффициенты синусной составляющей ряда Фурье
- 7. – номер гармоники – основная гармоника; – постоянная составляющая, нулевая гармоника ряда Фурье; – коэфициенты ряда
- 8. Вещественная форма ряда Фурье
- 10. Комплексная форма ряда Фурье Комплексные коэффициенты ряда Фурье: - комплексным частотным спектром Комплексная форма:
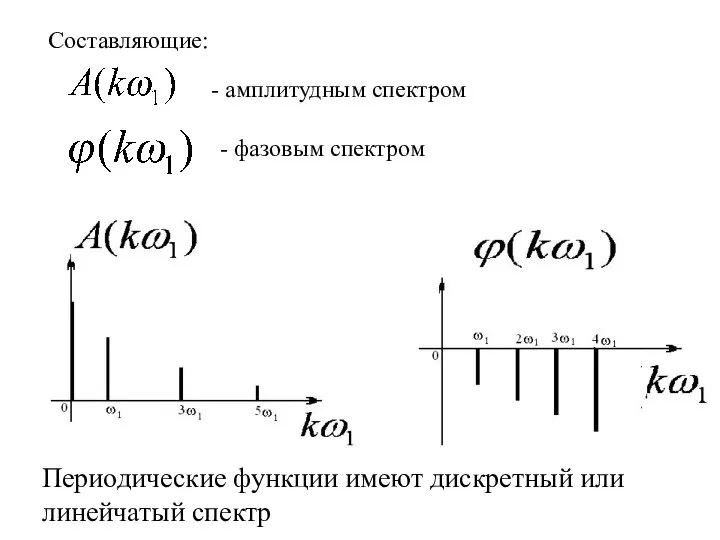
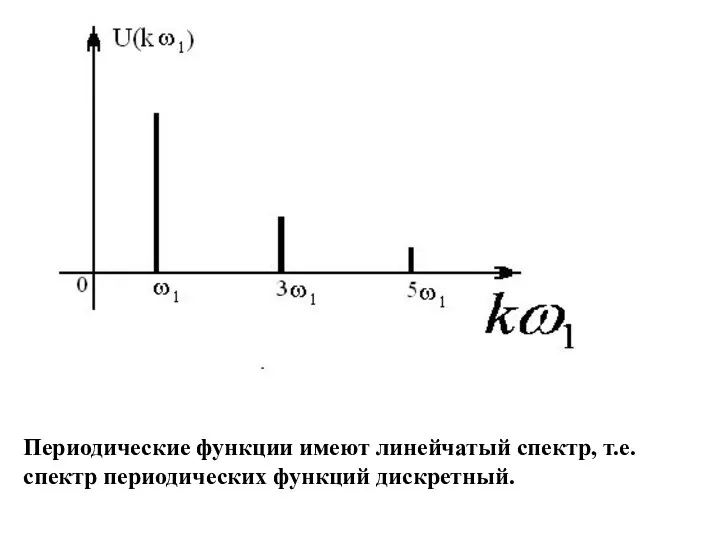
- 11. Составляющие: - амплитудным спектром - фазовым спектром Периодические функции имеют дискретный или линейчатый спектр
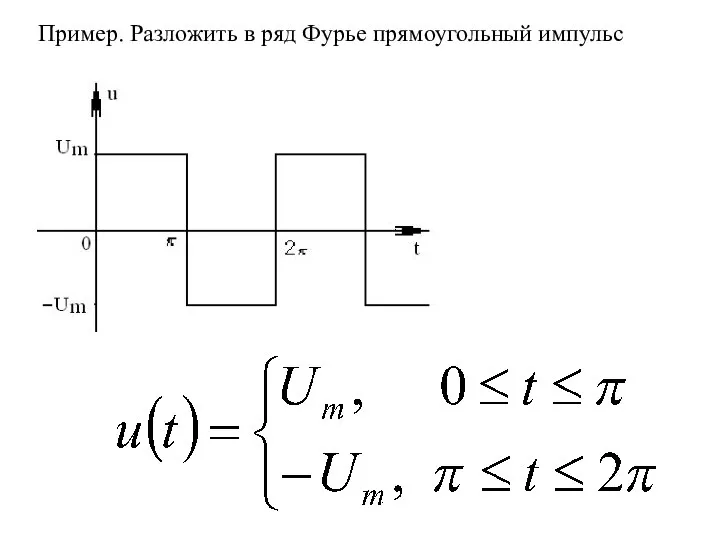
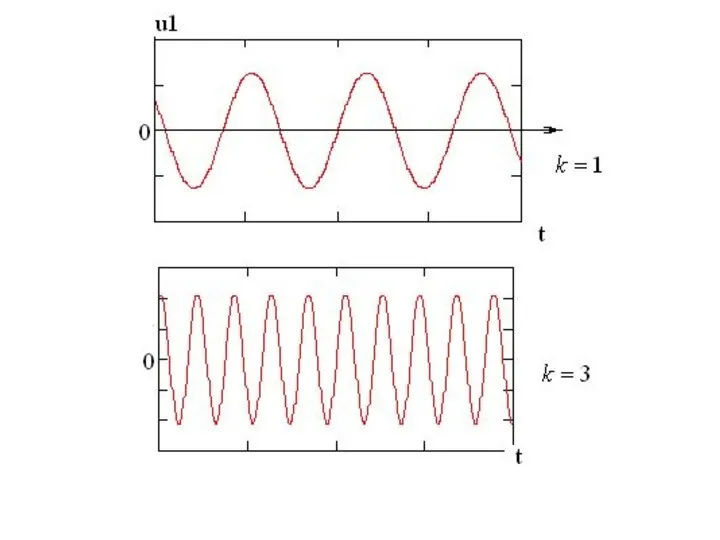
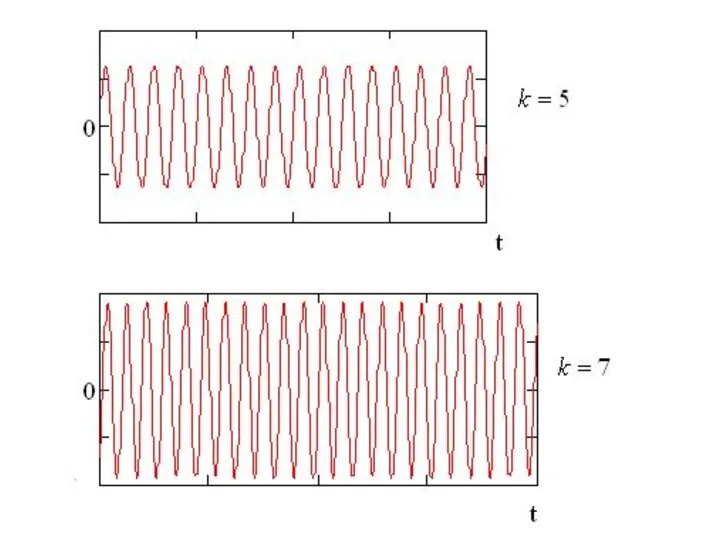
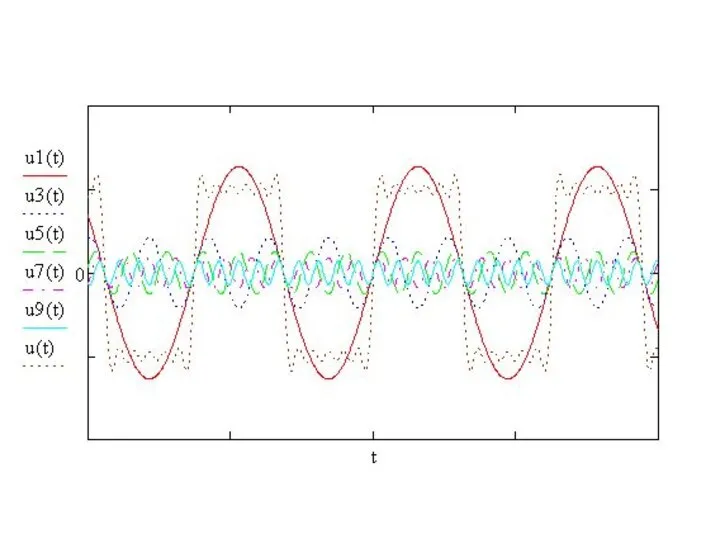
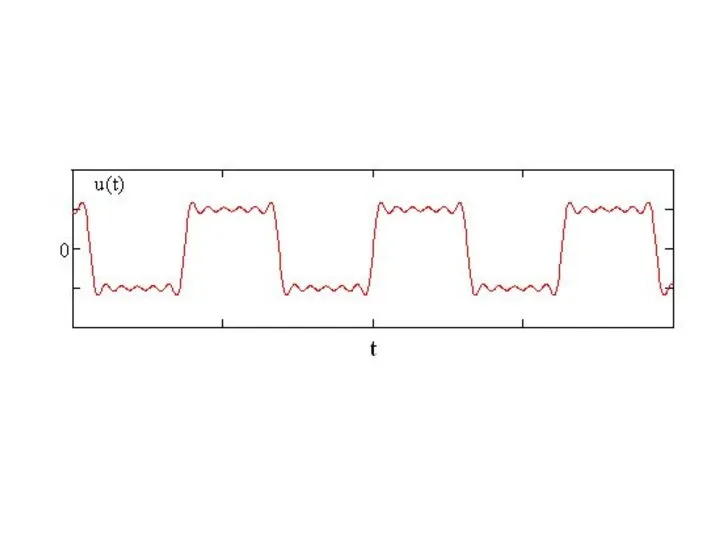
- 12. Пример. Разложить в ряд Фурье прямоугольный импульс
- 23. Периодические функции имеют линейчатый спектр, т.е. спектр периодических функций дискретный.
- 24. Спектр непериодических сигналов можно получить с помощью преобразования Фурье. Преобразование Фурье позволяет получить спектральные функции непериодических
- 25. Преобразование Фурье прямое двухстороннее преобразование Фурье Если выполняется условие: преобразование Фурье называется односторонним преобразование Фурье
- 26. непериодическая функция времени спектральная плотность, спектральная функция, спектр непериодической функции обратное преобразование Фурье
- 27. абсолютно интегрируемые функции в бесконечном интервале Преобразование Фурье – частный случай преобразования Лапласа при
- 28. непериодическая функция времени спектральная плотность, спектральная функция, спектр непериодической функции обратное преобразование Фурье
- 29. Эти формулы позволяют преобразовать непериодическую функцию времени в функцию частоты Так как спектральная функция комплексная величина,
- 30. Модуль называется амплитудный спектр, четная функция Аргумент называется фазовый спектр, нечетная функция.
- 31. 1. Определить спектр функции Изображение по Лапласу функции
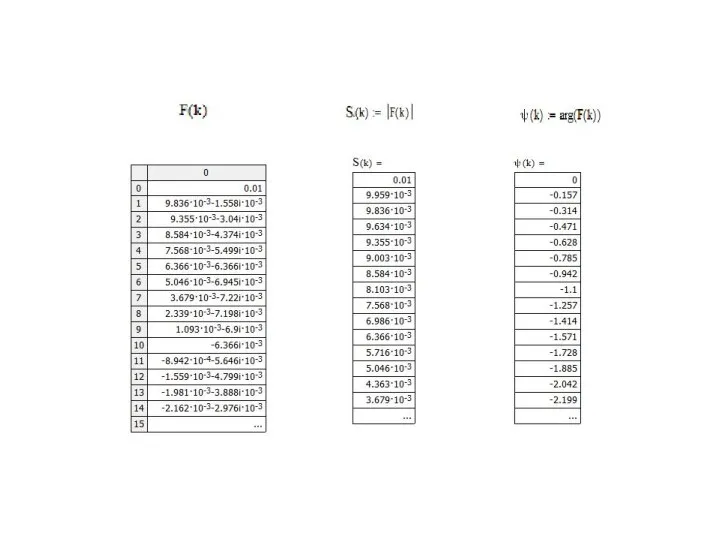
- 32. Спектральная функция: Фазовый спектр: Амплитудный спектр:
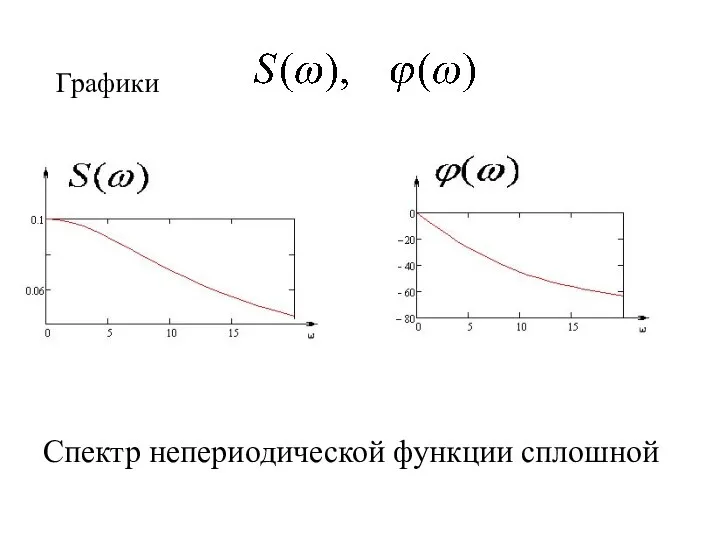
- 33. Графики Спектр непериодической функции сплошной
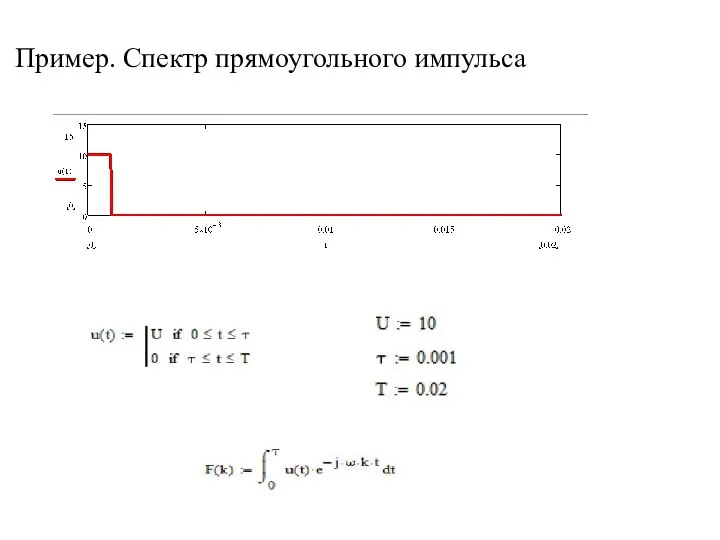
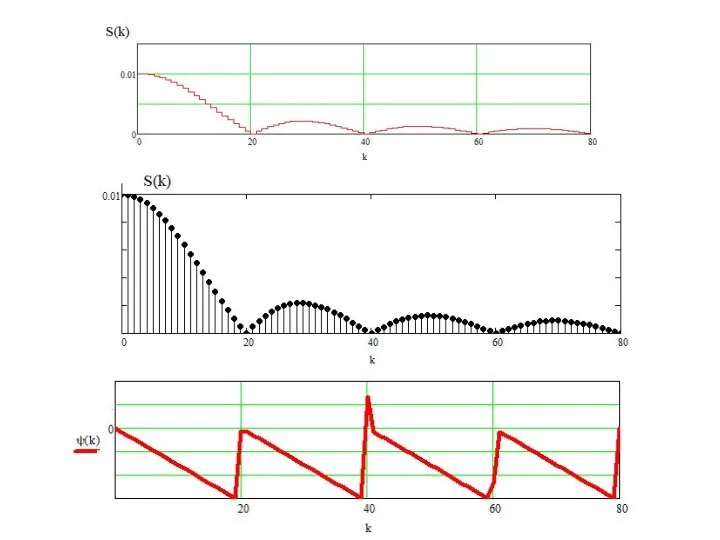
- 34. Пример. Спектр прямоугольного импульса
- 37. Спектр непериодической функции сплошной.
- 39. Скачать презентацию






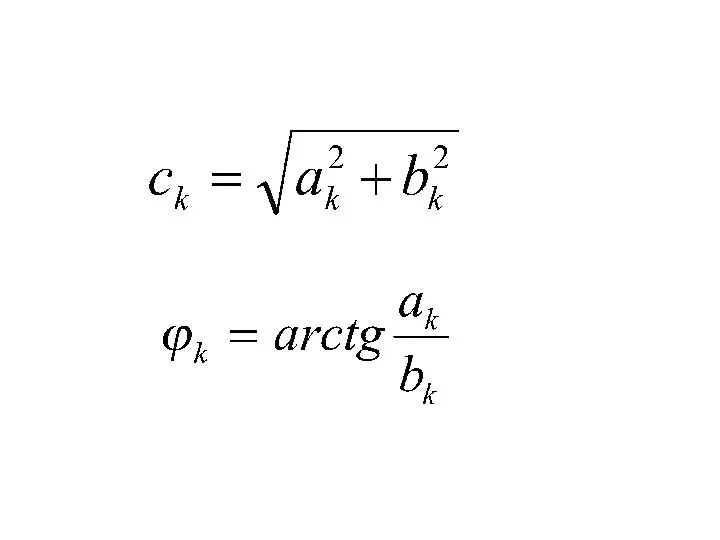

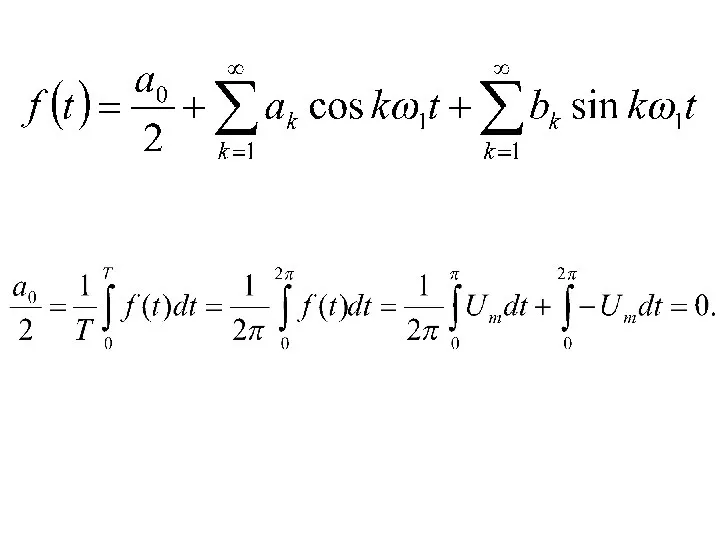
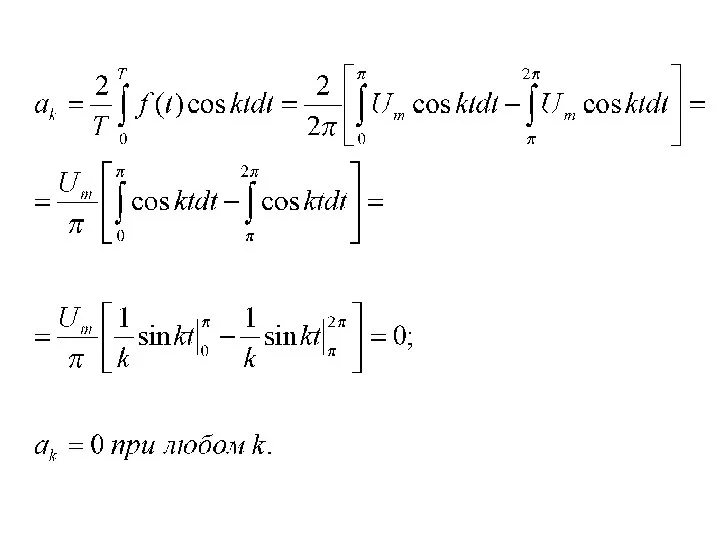
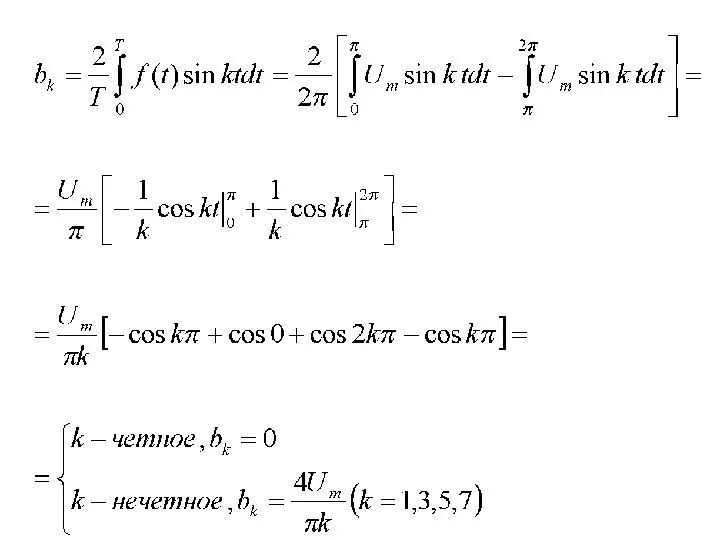
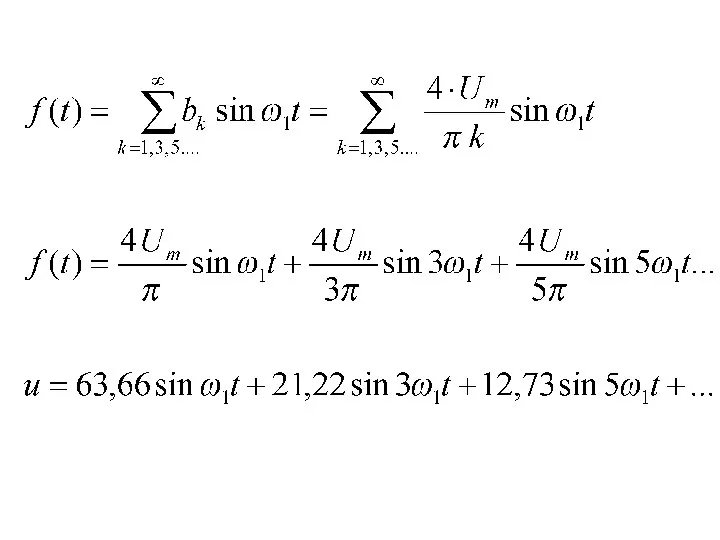












 Омск, проспект Губкина, д.1
Омск, проспект Губкина, д.1 Рыжие. Поцелованные солнцем
Рыжие. Поцелованные солнцем Учитель- профессия нужная, важная, самая главная на земле
Учитель- профессия нужная, важная, самая главная на земле Смысловые уровни вещей
Смысловые уровни вещей Презентация на тему "Причины плохого поведения ребенка" - скачать презентации по Педагогике
Презентация на тему "Причины плохого поведения ребенка" - скачать презентации по Педагогике Создание презентаций на ПК
Создание презентаций на ПК Контрольная работа №1 по ЛА и АГ_нов3
Контрольная работа №1 по ЛА и АГ_нов3 aa9c82ab93914bd3847e6c12db9c6ace
aa9c82ab93914bd3847e6c12db9c6ace Задачи в жизненных ситуациях
Задачи в жизненных ситуациях КРУГЛЫЙ СТОЛ «Состояние и перспективы развития профессионального образования в Кабардино-Балкарской Республике с учётом совр
КРУГЛЫЙ СТОЛ «Состояние и перспективы развития профессионального образования в Кабардино-Балкарской Республике с учётом совр Жизнь и творчество
Жизнь и творчество prezentatsia_vkr
prezentatsia_vkr Микросотовая система KIRK 500
Микросотовая система KIRK 500 Реализация личностно-ориентированного обучения в начальной школе
Реализация личностно-ориентированного обучения в начальной школе Использование системно-деятельностнoго подхода на уроках математики
Использование системно-деятельностнoго подхода на уроках математики основная часть урока
основная часть урока Подготовила учитель истории Подготовила учитель истории МОУ Талаканской СОШ №6 Черткова Ольга Александровна
Подготовила учитель истории Подготовила учитель истории МОУ Талаканской СОШ №6 Черткова Ольга Александровна Олимпийский урок
Олимпийский урок Резюме ФИО: Иванова Дарья Абрамовна Дата рождения:10 января, 1927 Место рождения: д. Челкума
Резюме ФИО: Иванова Дарья Абрамовна Дата рождения:10 января, 1927 Место рождения: д. Челкума Управленческая мысль в эпоху Европейского средневековья
Управленческая мысль в эпоху Европейского средневековья Presentation Title
Presentation Title  Аудит бренда. Шаблон
Аудит бренда. Шаблон Обмен веществ и энергии в клетке
Обмен веществ и энергии в клетке  Презентация на тему Типы изомерии
Презентация на тему Типы изомерии Презентация на тему Законы электролиза
Презентация на тему Законы электролиза Презентация на тему Геном человека
Презентация на тему Геном человека Дорогая наша Елена Николаевна!
Дорогая наша Елена Николаевна! МОУ СОШ №4 г.Всеволожска
МОУ СОШ №4 г.Всеволожска