Содержание
- 2. Элементы, из которых составлена матрица, называют элементами матрицы. Пример: – элемент первой строки и третьего столбца
- 3. квадратная порядка n Две матрицы A и B считаются равными, если они одинакового размера, и элементы,
- 4. 1. матрица – столбец длины m 2. матрица – строка длины n 3. нулевая матрица
- 5. 4. Условную линию в квадратной матрице порядка n, на которой расположены элементы a11, a22, … ,
- 6. 5. треугольные матрицы 6. трапециевидная матрица
- 7. 7. – ступенчатая – не ступенчатая
- 8. . (-1)A – противоположная матрице A -A
- 9. 1. 2. 3. 4. 5. 6. 7. 8.
- 10. .
- 11. Матрицы A и B, для которых AB=BA, называют перестановочными. 1. 2. 3. 4. AE= EA= A
- 12. Определение. Пусть A – матрица размера . Матрица размера , полученная из A заменой каждой ее
- 13. Факториал натурального числа n: n! 0!= 1 Расположение n чисел 1, 2, 3, …, n в
- 14. Определение. Пусть A – квадратная матрица порядка n. Определителем матрицы A (определителем порядка n) называется сумма
- 16. Определение. Пусть A – квадратная матрица порядка n. Определителем матрицы A (определителем порядка n) называется сумма
- 17. Правило треугольников:
- 18. Если все элементы k-той строки определителя |A| являются суммами двух элементов, то определи-тель равен сумме двух
- 19. 5. Определитель равен нулю если: а) он имеет строку (столбец), состоящую из нулей; б) он имеет
- 20. 6. 7.
- 21. Пусть A – матрица размера k – некоторое число, Определение. Выберем в матрице A произвольно k
- 22. Определение. Пусть A – квадратная матрица порядка n. Выберем в A минор k-го порядка Mk (выберем
- 23. Следствие (теоремы Лапласа). Определитель равен сумме произведений всех элементов любой строки (столбца) на их алгебраические дополнения,
- 24. = –102
- 25. Если А имеет обратную, то 1. А – квадратная. 2. Обратная матрица единственная. 3. Определитель матрицы
- 26. Теорема. Пусть А – квадратная матрица порядка n. Матрица A имеет обратную тогда и только тогда,
- 27. Определение. Рангом матрицы называют макси-мальный порядок ее миноров, отличных от нуля. Базисным минором матрицы называют её
- 28. Определение. Элементарными преобразованиями матрицы называются преобразования следующего вида: 1. умножение некоторой строки (столбца) на ненулевое число;
- 29. Определение. Матрица В называется эквивалентной матрице А, если она может быть получена из А эле-ментарными преобразованиями.
- 30. r(A) = 2 – базисный минор Пример
- 31. Определение. Строки (столбцы) S1, S2, … , Sk называют линейно зависимыми, если существуют числа α1, α2,
- 32. Лемма (о линейной зависимости). Строки (столбцы) S1, S2, … , Sk линейно зависимы тогда и только
- 33. Линейное уравнение – числа. – коэффициенты уравнения b – свободный член Если , то уравнение называют
- 34. Система m линейных уравнений с n неизвестными, т.е. система вида Тогда система принимает вид: AX =
- 35. Упорядоченный набор чисел c1, c2, …, cn называется решением системы (*), если он обращает в тож-дество
- 36. Теорема (Кронекера – Капелли). Система линейных уравнений (*) совместна тогда и только тогда, когда ранг матрицы
- 37. 1) Матричный метод Пусть m = n и . Системы такого вида называются невырожденными. 1. решение
- 38. 2) Метод Крамера Теорема (Крамера). Если в системе линейных урав-нений число уравнений m и число неизвестных
- 39. Пример
- 40. Определение. Элементарными преобразованиями системы линейных уравнений называются преобра-зования следующего вида: 1. умножение обеих частей уравнения на
- 41. Схема метода Гаусса. Прямой ход 1. Элементарными преобразованиями приводим систему к эквивалентной системе, имеющей расширенную матрицу
- 42. Обратный ход 5. Начиная с последнего уравнения (в обратном порядке) выражаем все зависимые переменные через свободные.
- 43. 1. 2. система совместна 3. 4. 5. – общее решение
- 44. (**) , т.е. система совместна – решение. Другие решения называют нетривиальными. Это решение называют нулевым или
- 45. С1, С2, … , Сk – матрицы-столбцы, являющиеся решениями системы (**) α1, α2, … , αk
- 46. Теорема (существования фундаментальной системы решений). Пусть r – ранг матрицы системы (**). Если система имеет нетривиальные
- 47. – общее решение 1) 3) 2) (1, 0, 1, 0, 0), (– 1, 1, 0, 1,
- 49. Скачать презентацию






















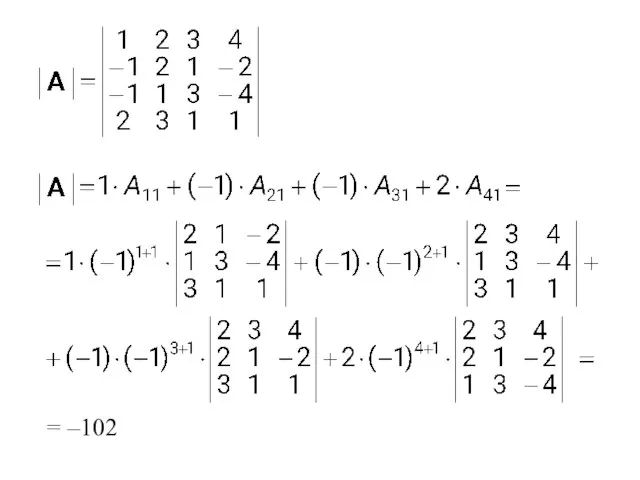























 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом