Содержание
- 2. Египет Решение экономических задач чиновниками Уравнения 1-й степени и простейшие квадратные уравнения Египетские водяные часы, реконструкция
- 3. Египет Папирус с математическими выкладками Число 35736, записанное египетскими иероглифами
- 4. Вавилон 60-ричная система счисления Задачи на уравнения 3-й, 4-й, 5-й степени Общие черты науки в Египте
- 5. Древняя Греция Милетская школа Фалес Иония V-Ivвв. до н.э. Анаксимен Анаксимандр
- 6. Древняя Греция Милетская школа Осмысление и обобщение результатов => возникновение доказательства Систематическое использование идеи доказательства Основы
- 7. Пифагореизм Пифагор Самосский ок. 580-500 до н.э. Практика «Пифагорейский образ жизни» Теория Учения Обряды «Число есть
- 8. Пифагореизм Исследование чисел натурального ряда Связи между четными и нечетными числами Доказана теорема Пифагора Построение 5-ти
- 9. Элейская школа Парменид (ок. 540-450 до н.э.) Зенон (ок.490-430 до н.э.) Доказательства против движения (движение до
- 10. Элейская школа Апории Зенона – связь с нахождением суммы бесконечной геометрической прогрессии Косвенное доказательство («от противного»)
- 11. Демокрит Концепция математического атомизма «Каноника» - свод основных принципов + физика и этика «Подлинное сущее» -
- 12. Платоновский идеализм В диалоге «Пир» - концепция пределов Арифметика, геометрия, астрономия и гармония – науки, данные
- 13. Философия математики Аристотеля Необходимость построения системы математических знаний Доказательство – процесс производства знаний из начал (труд
- 14. XIX в. Луи Пуансо «Философское осмысление математических проблем способно придать им более глубокое понимание» Феликс Клейн
- 15. Методологическая ценность философии для математики А. Эйнштейн: «Если под философией понимать поиск знания в его наиболее
- 16. Ну и наконец На заседании Нью-Йоркского математического общества, профессор Коул возвёл число 2 в 67-ю степень,
- 18. Скачать презентацию















 Морской флот. Морской транспорт и его деятельность
Морской флот. Морской транспорт и его деятельность Ресторан и мини-гольф клуб Мелисса Флеминг
Ресторан и мини-гольф клуб Мелисса Флеминг Электронагревательные приборы. 8 класс
Электронагревательные приборы. 8 класс Не поддаваться панике
Не поддаваться панике Бозгурд. Терроризм
Бозгурд. Терроризм Презентация на тему Развитие сюжетной игры детей дошкольного возраста
Презентация на тему Развитие сюжетной игры детей дошкольного возраста Инновационные подходы к социально-воспитательной работе с детьми с ограниченными возможностями здоровья
Инновационные подходы к социально-воспитательной работе с детьми с ограниченными возможностями здоровья Продукция
Продукция Пути развития современной архитектуры. Основные стили архитектуры ХХ-ХXI века. 7 класс
Пути развития современной архитектуры. Основные стили архитектуры ХХ-ХXI века. 7 класс Страны Южной Америки
Страны Южной Америки МОУ "Берёзовская средняя общеобразовательная школа №2"
МОУ "Берёзовская средняя общеобразовательная школа №2" Презентация на тему Симметрия в архитектуре
Презентация на тему Симметрия в архитектуре  Protected Area Governance
Protected Area Governance  Что такое фольклор?
Что такое фольклор? Культурные практики ребенка
Культурные практики ребенка Основы трудового права
Основы трудового права  Инновационная экосистема
Инновационная экосистема Реконкиста и образование централизованных государств на Пиренейском полуострове
Реконкиста и образование централизованных государств на Пиренейском полуострове Птицы
Птицы Особенности органищации БУ в группах
Особенности органищации БУ в группах Архитектура Акрополя
Архитектура Акрополя Правописание безударных личных окончаний глаголов I и I I спряжения
Правописание безударных личных окончаний глаголов I и I I спряжения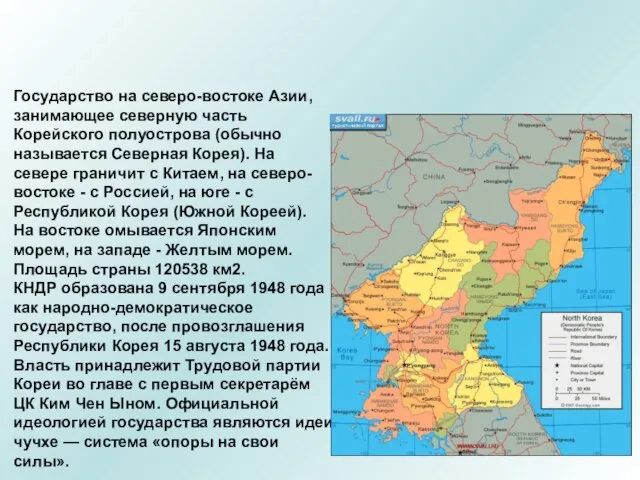 Презентация на тему СЕВЕРНАЯ КОРЕЯ (КОРЕЙСКАЯ НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА)
Презентация на тему СЕВЕРНАЯ КОРЕЯ (КОРЕЙСКАЯ НАРОДНО-ДЕМОКРАТИЧЕСКАЯ РЕСПУБЛИКА)  Нормативно-правовое обеспечение организации производственного контроля на молокоперерабатывающих предприятиях
Нормативно-правовое обеспечение организации производственного контроля на молокоперерабатывающих предприятиях Типы смесителей. Лекция №10
Типы смесителей. Лекция №10 Безопасный вебсерфинг
Безопасный вебсерфинг Курообразные
Курообразные Группа «Дюймовочка»
Группа «Дюймовочка»