Содержание
- 2. Тема урока: Уравнения, приводимые к квадратным. Цели урока: повторить способы решения уравнений, приводимых к квадратным; развивать
- 3. Сципион дель Ферро (итал. Scipione del Ferro, 6 февраля 1465, Болонья, северная Италия — 5 ноября
- 4. Никколо Тарталья (итал. Niccolò Fontana Tartaglia, 1499—1557) — итальянский математик. Биография Родился в Брешии. Истинная фамилия
- 5. Джероламо Кардано (лат. Hieronymus Cardanus, итал. Girolamo Cardano, Gerolamo Cardano; 24 сентября 1501, Павия — 21
- 6. Рафаэль Бомбелли (итал. Rafael Bombelli; ок. 1526, Болонья — 1572, вероятно, Рим) — итальянский математик, инженер-гидравлик.
- 8. I. Устная работа Какие из чисел: -3; -2; -1; 0; 1; 2; 3 являются корнями уравнения:
- 9. II. Практическая работа 25х³ - 50х² - х + 2 = 0 х³ -х² - 4(х-1)²
- 10. III. Самостоятельная работа I вариант Решите уравнения: а) у³ - 16у = 0; б) х4 –
- 12. Скачать презентацию









 А.С.Пушкин краткая биография
А.С.Пушкин краткая биография  - программастратегического назначения
- программастратегического назначения Гарантийные письма – ГП
Гарантийные письма – ГП COUNTING FROM ZERO TO TEN ZERO
COUNTING FROM ZERO TO TEN ZERO Агрессивность в поведении детей
Агрессивность в поведении детей Автогалерея
Автогалерея Техника Изонить
Техника Изонить «Очистка воздушных масс»
«Очистка воздушных масс»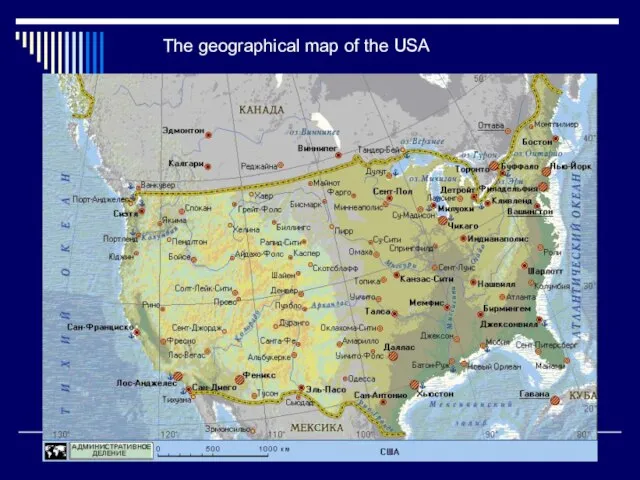 The geographical map of the USA
The geographical map of the USA Coffemar S500
Coffemar S500 Чемпионат мира по футболу 2018
Чемпионат мира по футболу 2018 Презентация на тему Соломон
Презентация на тему Соломон История чемпионата мира
История чемпионата мира Гранатовый браслет
Гранатовый браслет Art & Literature
Art & Literature Аппликация из ткани
Аппликация из ткани Повышение качества жизни трудящихся как фактор в реализации социальной политики развития российского Дальнего Востока
Повышение качества жизни трудящихся как фактор в реализации социальной политики развития российского Дальнего Востока Принципы разработки норм содержания пути для высокоскоростного движения
Принципы разработки норм содержания пути для высокоскоростного движения Полное товарищество
Полное товарищество Весна, чудо, девушка. Фотопроект
Весна, чудо, девушка. Фотопроект Почему учащиеся не хотят заниматься физической культурой
Почему учащиеся не хотят заниматься физической культурой Аудит затрат. Лекция 11
Аудит затрат. Лекция 11 семинар 2 - кинестетика
семинар 2 - кинестетика Торговая Марка«Антон Палыч»
Торговая Марка«Антон Палыч» СЕМИНАРДеятельностный подход к образованию в новых образовательных стандартах(начальные классы)
СЕМИНАРДеятельностный подход к образованию в новых образовательных стандартах(начальные классы) Откуда флаг пришёл?
Откуда флаг пришёл? London Quiz
London Quiz Мерчандайзинг
Мерчандайзинг