Метод интервалов

СОДЕРЖАНИЕ:
ФУНКЦИИ.
АЛГОРИТМ.
ПРОВЕРЬ СВОИ СИЛЫ:
8 КЛАСС
9 КЛАСС
10-11 КЛАСС

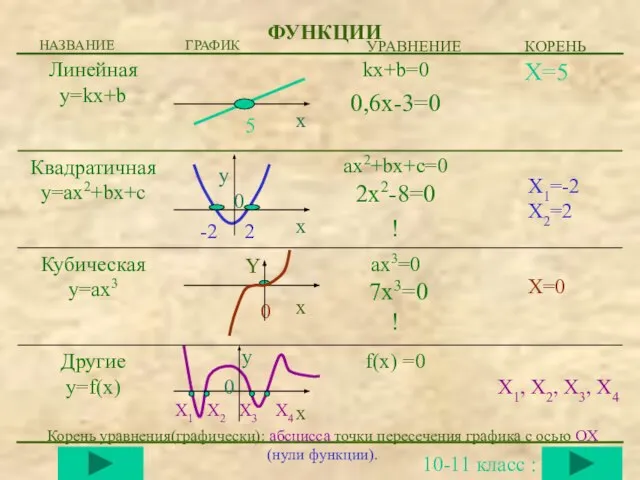
ФУНКЦИИ
f(x) =0
ax3=0
7x3=0
!
ax2+bx+c=0
2x2-8=0
!
X=5
kx+b=0
0,6x-3=0
5
X1=-2
X2=2
X=0
X1, X2, X3, X4
НАЗВАНИЕ ГРАФИК
УРАВНЕНИЕ КОРЕНЬ
x
x
x
x
Y
Корень уравнения(графически): абсцисса точки пересечения графика с осью OX (нули функции).
10-11 класс :
у
0

-2П -П П
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
f(Х) =0
tq(Х)=0
sin(Х) =0
!
loq2(x) =0
loq2(x) =loq21
!
X: нет
корней
0,5Х=0
X=1
X=Пk,
k R
X=Пk,
k R
НАЗВАНИЕ СХЕМА ГРАФИКА
УРАВНЕНИЕ КОРЕНЬ
X
X
X
Y
Корень уравнения(графически): абсцисса точки пересечения графика с осью OX (нули функции).
Y
1
1
0
Y
0

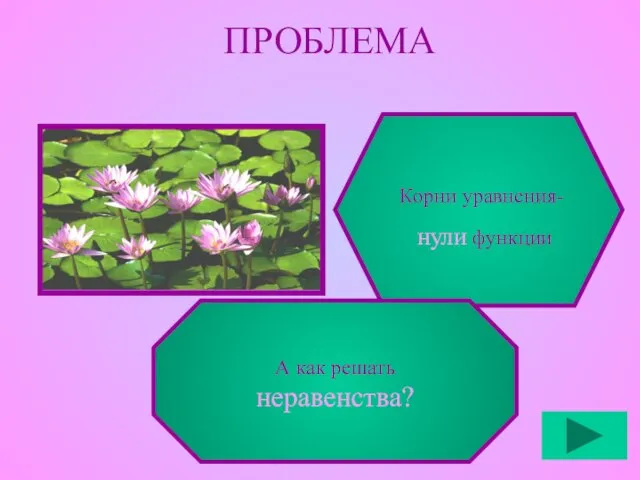
Корни уравнения-
нули функции
А как решать
неравенства?
ПРОБЛЕМА

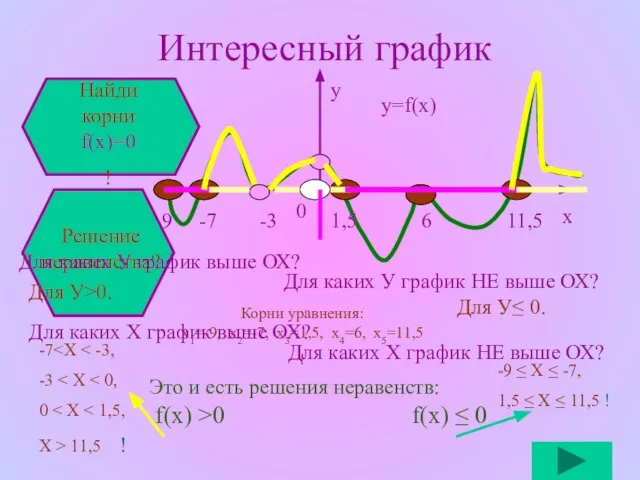
Интересный график
у=f(x)
Найди корни f(x)=0
!
Корни уравнения:
х1=-9, х2=-7, х3=1,5, х4=6, х5=11,5
!
Решение
неравенства?
Для каких У график выше ОХ?
Для У>0.
Для каких Х график выше ОХ?
-7<Х < -3,
-3 < Х < 0,
0 < Х < 1,5,
Х > 11,5 !
Для каких У график НЕ выше ОХ?
Для У≤ 0.
Для каких Х график НЕ выше ОХ?
-9 ≤ Х ≤ -7,
1,5 ≤ Х ≤ 11,5 !
Это и есть решения неравенств:
f(x) >0 f(x) ≤ 0

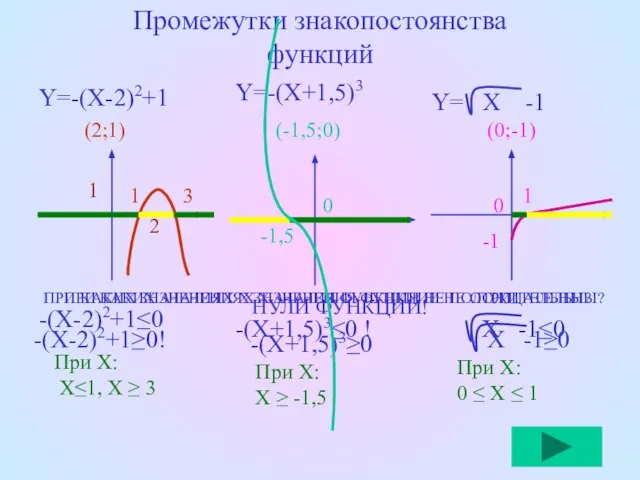
-(X-2)2+1≤0
-(X-2)2+1≥0!
-(X+1,5)3≥0
ПРИ КАКИХ ЗНАЧЕНИЯХ Х ЗНАЧЕНИЯ ФУНКЦИИ НЕ ОТРИЦАТЕЛЬНЫ?
ПРИ КАКИХ ЗНАЧЕНИЯХ Х ЗНАЧЕНИЯ ФУНКЦИИ НЕ ПОЛОЖИТЕЛЬНЫ?
Промежутки знакопостоянства
функций
-(X+1,5)3≤0 !
Y=-(X+1,5)3
Y=-(X-2)2+1
НУЛИ ФУНКЦИЙ!
При Х:
Х≤1, Х ≥ 3
При Х:
Х ≥ -1,5
При Х:
0 ≤ Х ≤ 1
2
-1,5
-1
(2;1)
(-1,5;0)
(0;-1)
1 3
1
1
0
0

Корни уравнения-
нули функции
А как решать
неравенства?
ПРОБЛЕМА!
Найти промежутки знакопостоянства функции
( Ответить на вопрос: при каких значениях Х график функции расположен выше, ниже или
пересекает ось ОХ ?)
!
СНЯТА

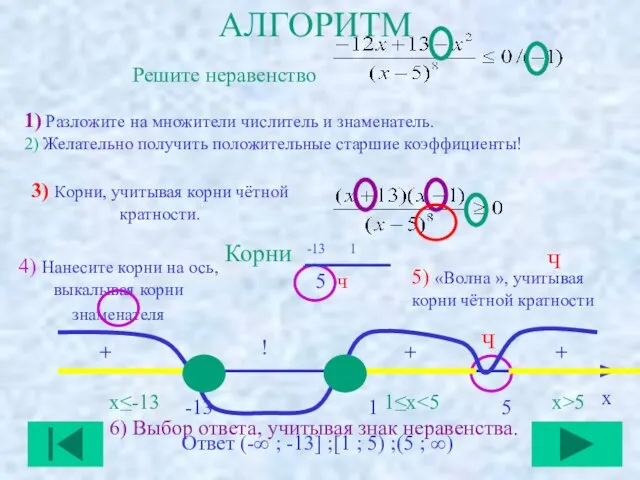
АЛГОРИТМ
Решите неравенство
1) Разложите на множители числитель и знаменатель.
2) Желательно получить положительные старшие коэффициенты!
3) Корни, учитывая корни чётной кратности.
Корни --13-----1-----
5 ч
4) Нанесите корни на ось, выкалывая корни знаменателя
x
5) «Волна », учитывая корни чётной кратности
-13 1 5
Ч
!
Ч
6) Выбор ответа, учитывая знак неравенства.
x≤-13 1≤x<5 x>5
Ответ (-∞ ; -13] ;[1 ; 5) ;(5 ; ∞)
+ + +
+ + +

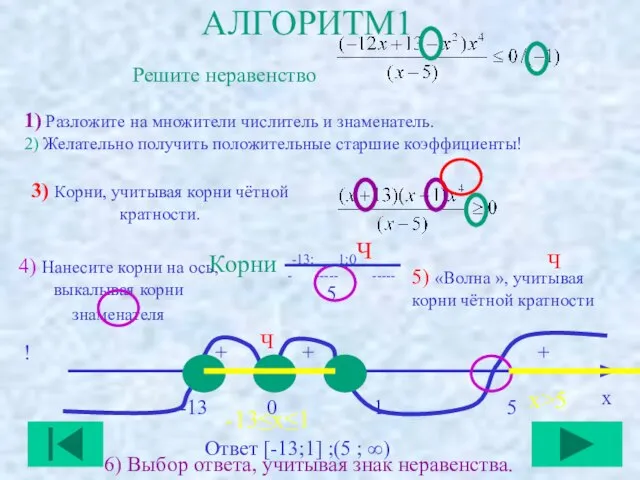
-13≤x≤1
АЛГОРИТМ1
Решите неравенство
1) Разложите на множители числитель и знаменатель.
2) Желательно получить положительные старшие коэффициенты!
3) Корни, учитывая корни чётной кратности.
Корни --13;-----1;0Ч-----
5
4) Нанесите корни на ось, выкалывая корни знаменателя
x
5) «Волна », учитывая корни чётной кратности
-13 0 1 5
Ч
!
Ч
6) Выбор ответа, учитывая знак неравенства.
Ответ [-13;1] ;(5 ; ∞)
+ + +
x>5

ПРИМЕРЫ
Найти ООФ
Корни
-6 -4 4 25
!
!
!
-6≤x<-4; 4
Ответ [-6;-4); (4;25]
+
+
Подсказка?
Алгоритм?
-x4+5x2+36≤0
x4-5x2-36≤0
(x-2)(x+2) (x2+9) ≤ 0
_
-2≤x≤2
Ответ [-2;2]
При каких значениях аргумента Х
существует функция (Y)?

РЕШЕНИЕ
1)Подкоренное выражение корня чётной степени не отрицательное.
2)Знаменатель не может быть 0.
Решить первое ,
решить второе,
выбрать общее.
+
+
2
Что является решением
этой системы ?
!
Ответ: [-3;2); (2;+∞)
-3≤x<2, x>2
!

+
ПРИМЕРЫ1
Найти ООФ
Корни
-6 -4 4 25
!
!
!
-6
Ответ [-6;-4); (4;25]
+
_
Ответ [-2;2]
-x4+5x2+36≤0
(x-2)(x+2) (x2+9) ≤ 0

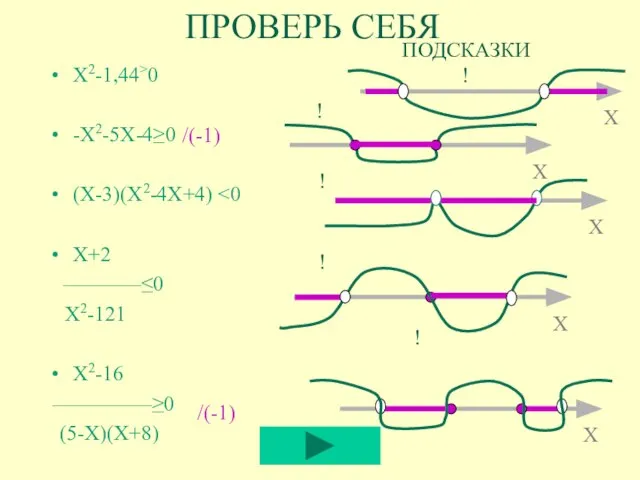
ПРОВЕРЬ СЕБЯ
Х2-1,44>0
-Х2-5Х-4≥0
(Х-3)(Х2-4Х+4) <0
Х+2
___________≤0
Х2-121
Х2-16
______________≥0
(5-Х)(Х+8)
ПОДСКАЗКИ
!
!
!
/(-1)
/(-1)

ПРОВЕРЬ СЕБЯ:
ОТВЕТЫ.
(-∞;1,2); (1,2;∞)
[-4;-1]
(-∞; 2); (2;3)
(-∞; -11); [-2; 11)
(-8;-4); [4; 5)
5
УРА
ХОРОШО
2;3 ОШИБКИ
ТРОЕЧКА
БОЛЬШЕ ТРЁХ
ОШИБОК ?

ПРОВЕРЬ СВОИ СИЛЫ:
8 КЛАСС
9 КЛАСС
10-11 КЛАСС

8 КЛАСС
х2-2х ≥0
х2-2x-3<0
-x2+169>0
(x+3)(x-4) ≤0
x+3
≥0 !
x-4
6. (x+5)2(x-1) ≥0
7. (x-3)(x+2)12(x-5) ≤0
8. (3-x)(x+2)>0
9. –x2-4x-4>0
10. (7-x)(x2+6x+9)>0
Решите неравенства МЕТОДОМ ИНТЕРВАЛОВ

9 КЛАСС
При каких значениях X
существует выражение?
Найдите ООФ
!

ООФ: У=loq0,5X , Х>0
10-11 КЛАСС
ВАЖНО: ООФ, ОЗФ, МОНОТОННОСТЬ
У=loq0,5X
!
!
!
-2≤X<-1
(-2;-1]!
-1
(-1 ;2)!
х≥4
[4;+∞)
!
0
X≥-1

ЗАДАНИЕ (10-11)
ВАЖНО: ООФ, ОЗФ, МОНОТОННОСТЬ
ПОДСКАЗКИ
Решите неравенства, пользуясь
МЕТОДОМ ИНТЕРВАЛОВ